Антиматроид - Antimatroid

Три представления антиматроида: порядок включения в его семействе допустимых множеств, формальный язык и соответствующий poset путей.

В математика, антиматроид это формальная система который описывает процессы, в которых набор создается путем включения элементов по одному, и в котором элемент, будучи доступным для включения, остается доступным до тех пор, пока не будет включен. Антиматроиды обычно аксиоматизируется двумя эквивалентными способами, либо как установить систему моделирование возможных состояний такого процесса, или как формальный язык моделирование различных последовательностей, в которые могут быть включены элементы.Дилворт (1940) был первым, кто изучал антиматроидов, используя еще одну аксиоматизацию, основанную на теория решетки, и они часто открывались заново в других контекстах;[1] см. Korte et al. (1991) за исчерпывающий обзор теории антиматроидов со многими дополнительными ссылками.

Аксиомы, определяющие антиматроидов как установленные системы, очень похожи на аксиомы матроиды, но в то время как матроиды определяются аксиома обмена (например, базисный обмен, или независимый обмен множеством аксиомы), антиматроиды вместо этого определяются антиобменная аксиома, от которого и произошло их название. Антиматроиды можно рассматривать как частный случай гридоиды и из полумодульные решетки, и как обобщение частичные заказы и из распределительные решетки. Антиматроиды эквивалентны, по дополнение, чтобы выпуклые геометрии, комбинаторная абстракция выпуклые множества в геометрия.

Антиматроиды были применены для моделирования ограничений приоритета в проблемы с расписанием, потенциальные последовательности событий в симуляциях, планирование задач в искусственный интеллект, и состояния знаний учащихся-людей.

Определения

Антиматроида можно определить как конечное семейство F наборов, называемых возможные наборы, со следующими двумя свойствами:

  • В союз любых двух допустимых множеств также допустима. Это, F является закрыто под союзами.
  • Если S непустое допустимое множество, то существует Икс в S такой, что S \ {Икс} (множество, образованное удалением Икс от S) также возможно. Это, F является доступная система наборов.

У антиматроидов также есть эквивалентное определение как формальный язык, то есть как набор струны определенный из конечного алфавита символы. Язык L определение антиматроида должно удовлетворять следующим свойствам:

  • Каждый символ алфавита встречается хотя бы в одном слове L.
  • Каждое слово L содержит не более одной копии любого символа.
  • Каждые приставка строки в L также в L.
  • Если s и т струны в L, и s содержит хотя бы один символ, которого нет в т, то есть символ Икс в s такой, что tx это еще одна строка в L.

Если L является антиматроидом, определенным как формальный язык, тогда наборы символов в строках L образуют доступную систему замкнутых множеств. В обратном направлении, если F является доступной системой замкнутых множеств, а L это язык струнных s с тем свойством, что набор символов в каждом префиксе s возможно, тогда L определяет антиматроид. Таким образом, эти два определения приводят к математически эквивалентным классам объектов.[2]

Примеры

Последовательность обстрела плоского набора точек. Сегменты линии показывают края выпуклые оболочки после того, как некоторые точки были сняты.
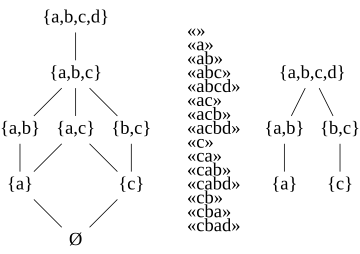
  • А цепь антиматроид имеет в качестве формального языка префиксы одного слова и, по мере возможности, устанавливает наборы символов в этих префиксах. Например, цепной антиматроид, определяемый словом «abcd», имеет в качестве своего формального языка строки {ε, «a», «ab», «abc», «abcd»} и в качестве возможного устанавливает множества Ø, {a} , {a, b}, {a, b, c} и {a, b, c, d}.[3]
  • А посет антиматроид имеет, как это возможно, устанавливает нижние наборы конечного частично заказанный набор. От Теорема Биркгофа о представлении для дистрибутивных решеток допустимые множества в антиматроиде poset (упорядоченные по включению множества) образуют дистрибутивную решетку, и таким образом может быть сформирована любая дистрибутивная решетка. Таким образом, антиматроиды можно рассматривать как обобщения дистрибутивных решеток. Цепной антиматроид - это частный случай антиматроида позета для общий заказ.[3]
  • А последовательность обстрелов конечного множества U очков в Евклидова плоскость или многомерный Евклидово пространство порядок точек такой, что для каждой точки п, Существует линия (в евклидовой плоскости или гиперплоскость в евклидовом пространстве), который разделяет п со всех последующих точек в последовательности. Эквивалентно, п должен быть вершиной выпуклая оболочка этого и всех последующих пунктов. Последовательности частичного обстрела набора точек образуют антиматроид, называемый обстрел антиматроида. Возможные комплексы обстреливающего антиматроида: перекрестки из U с дополнять выпуклого множества.[3] Каждый антиматроид изоморфен антиматроиду-оболочке из точек в достаточно многомерном пространстве.[4]
  • А идеальный порядок исключения из хордовый граф порядок его вершин такой, что для каждой вершины v, соседи v которые происходят позже, чем v в форме заказа клика. Префиксы порядков идеального исключения хордального графа образуют антиматроид.[3] Антиматроиды также описывают некоторые другие виды порядков удаления вершин в графах, такие как порядок удаления вершин. графики выигрыша.

Пути и основные слова

В теоретико-множественной аксиоматизации антиматроида есть некоторые специальные множества, называемые пути которые определяют весь антиматроид, в том смысле, что наборы антиматроида представляют собой в точности объединения путей. Если S любой возможный набор антиматроида, элемент Икс что может быть удалено из S образовать другой допустимый набор называется конечная точка из S, а допустимый набор, имеющий только одну конечную точку, называется дорожка антиматроида. Семейство путей можно частично упорядочить включением множества, образуя путь посеть антиматроида.

Для каждого возможного набора S в антиматроиде, и каждый элемент Икс из S, можно найти подмножество путей S для которого Икс является конечной точкой: для этого удаляйте по одному элементы, кроме Икс до тех пор, пока такое удаление не останется из допустимого подмножества. Следовательно, каждое допустимое множество в антиматроиде является объединением его подмножеств путей. Если S не является путем, каждое подмножество в этом объединении является правильное подмножество из S. Но если S сам по себе путь с конечной точкой Икс, каждое собственное подмножество S что принадлежит антиматроиду исключает Икс. Следовательно, пути антиматроида - это как раз те множества, которые не равны объединениям их собственных подмножеств в антиматроиде. Эквивалентно данное семейство наборов п образует множество путей антиматроида тогда и только тогда, когда для каждого S в п, объединение подмножеств S в п имеет на один элемент меньше, чем S сам. Если так, F сам является семейством объединений подмножеств п.

В формальной языковой формализации антиматроида мы также можем идентифицировать подмножество слов, которые определяют весь язык, т.е. основные слова.Самые длинные струны в L называются основные слова; каждое основное слово образует перестановку всего алфавита. Например, основные слова антиматроида poset - это линейные расширения данного частичного заказа. Если B это набор основных слов, L можно определить из B как набор префиксов слов в B. Часто таким образом удобно определять антиматроидов с помощью основных слов, но нелегко написать аксиоматическое определение антиматроидов с помощью их основных слов.

Выпуклая геометрия

Смотрите также: Выпуклый набор, Выпуклая геометрия, и Оператор закрытия

Если F система множеств, определяющая антиматроида, с U равный объединению множеств в F, то семейство множеств

дополнительный на наборы в F иногда называют выпуклая геометрия и наборы в г называются выпуклые множества. Например, в антиматроиде-снаряде выпуклые множества являются пересечениями U с выпуклыми подмножествами евклидова пространства, в которые U встроен.

В дополнение к свойствам систем множеств, которые определяют антиматроидов, система множеств, определяющая выпуклую геометрию, должна быть замкнута относительно пересечений и для любого множества S в г это не равно U должен быть элемент Икс не в S что можно добавить к S сформировать еще один набор в г.

Выпуклая геометрия также может быть определена в терминах оператор закрытия τ, который отображает любое подмножество U к его минимальному закрытому надмножеству. Чтобы быть оператором замыкания, τ должно обладать следующими свойствами:

  • τ (∅) = ∅: замыкание пустой набор пусто.
  • Любой набор S является подмножеством τ (S).
  • Если S это подмножество Т, то τ (S) должно быть подмножеством τ (Т).
  • Для любого набора S, τ (S) = τ (τ (S)).

Семейство замкнутых множеств, возникающих в результате операции замыкания этого типа, обязательно замкнуто относительно пересечений. Операторы замыкания, определяющие выпуклые геометрии, также удовлетворяют дополнительному антиобменная аксиома:

  • Если y ≠ z, и ни один из них не принадлежит τ (S), но z принадлежит τ (S ∪ {y}), тогда y не принадлежит τ (S ∪ {z}).

Операция замыкания, удовлетворяющая этой аксиоме, называется закрытие против обмена. Если S является замкнутым множеством в антиобменном замыкании, то аксиома антиобмена определяет частичный порядок на элементах, не принадлежащих S, где Икс ≤ y в частичном порядке, когда Икс принадлежит τ (S ∪ {y}). Если Икс является минимальным элементом этого частичного порядка, то S ∪ {Икс} закрыто. То есть, семейство замкнутых множеств антиобменного замыкания обладает тем свойством, что для любого множества, отличного от универсального, существует элемент Икс которые можно добавить к нему, чтобы получить еще один закрытый набор. Это свойство является дополнительным к свойству доступности антиматроидов, и тот факт, что пересечения замкнутых множеств замкнуты, дополняет свойство, что объединение допустимых множеств в антиматроиде возможно. Следовательно, дополнения замкнутых множеств любого антиобменного замыкания образуют антиматроид.[5]

В неориентированные графы в котором выпуклые множества (подмножества вершин, содержащие все кратчайшие пути между вершинами в подмножестве) образуют выпуклую геометрию, в точности Птолемеевы графы.[6]

Дистрибутивные решетки

Любые два набора в антиматроиде имеют уникальный наименьшая верхняя граница (их союз) и уникальный наибольшая нижняя граница (объединение наборов антиматроида, содержащихся в них обоих). Поэтому наборы антиматроида, частично заказанный путем включения множества образуют решетка. Различные важные особенности антиматроида можно интерпретировать в терминах теории решетки; например, пути антиматроида - это неприводимый к соединению элементы соответствующей решетки, а основные слова антиматроида соответствуют максимальные цепи в решетке. Решетки, возникающие из антиматроидов таким образом, обобщают конечный распределительные решетки, и его можно охарактеризовать по-разному.

  • Описание, первоначально рассмотренное Дилворт (1940) заботы неприводимый к встречам элементы решетки. Для каждого элемента Икс антиматроида существует единственное максимально допустимое множество SИкс что не содержит Икс (SИкс объединение всех допустимых множеств, не содержащих Икс). SИкс является неприводимым, что означает, что это не пересечение любых двух больших элементов решетки: любое большее допустимое множество и любое пересечение больших допустимых множеств содержит Икс и так не равно SИкс. Любой элемент любой решетки может быть разложен как пересечение несовместимых множеств, часто несколькими способами, но в решетке, соответствующей антиматроиду, каждый элемент Т имеет единственное минимальное семейство встречно неприводимых множеств SИкс чья встреча Т; это семейство состоит из множеств SИкс такой, что Т ∪ {Икс} принадлежит к антиматроидам. То есть решетка имеет уникальные встречно-неприводимые разложения.
  • Вторая характеристика касается интервалы в решетке подрешетки, определяемые парой элементов решетки Икс ≤ y и состоящий из всех элементов решетки z с участием Икс ≤ z ≤ y. Интервал атомистический если каждый элемент в нем представляет собой соединение атомов (минимальные элементы над нижним элементом Икс), и это Булево если он изоморфен решетке все подмножества конечного множества. Для антиматроида каждый атомистический интервал также является логическим.
  • В-третьих, решетки, возникающие из антиматроидов, имеют вид полумодульные решетки, решетки, удовлетворяющие верхний полумодулярный закон что для любых двух элементов Икс и y, если y крышки Икс ∧ y тогда Икс ∨ y крышки Икс. Перевод этого условия в наборы антиматроида, если набор Y имеет только один элемент, не принадлежащий Икс тогда этот один элемент может быть добавлен к Икс чтобы сформировать еще один набор в антиматроиде. Кроме того, решетка антиматроида имеет встречно-полураспределительное свойство: для всех элементов решетки Икс, y, и z, если Икс ∧ y и Икс ∧ z оба равны, то они также равны Икс ∧ (y ∨ z). Полумодулярная и встречно-полудистрибутивная решетка называется объединенно-распределительная решетка.

Эти три характеристики эквивалентны: любая решетка с уникальными встречно-неприводимыми разложениями имеет булевы атомистические интервалы и является объединенно-дистрибутивной, любая решетка с булевыми атомистическими интервалами имеет уникальные встречно-неприводимые разложения и является объединенно-дистрибутивной, и любая объединенно-дистрибутивная решетка имеет уникальные встречающиеся неприводимые разложения и булевы атомистические интервалы.[7] Таким образом, мы можем называть решетку с любым из этих трех свойств дистрибутивной по объединению. Любой антиматроид порождает конечную объединенно-дистрибутивную решетку, и любая конечная объединенно-распределительная решетка происходит от антиматроида таким образом.[8] Другой эквивалентной характеристикой конечных дистрибутивных решеток является то, что они оцененный (любые две максимальные цепи имеют одинаковую длину), а длина максимальной цепи равна количеству встречно неприводимых элементов решетки.[9] Антиматроид, представляющий конечную объединенно-распределительную решетку, может быть восстановлен из решетки: элементы антиматроида можно принять как встречно-неприводимые элементы решетки, а допустимое множество, соответствующее любому элементу Икс решетки состоит из множества встречно неприводимых элементов y такой, что y не больше или равно Икс в решетке.

Такое представление любой конечной дистрибутивной решетки как доступного семейства множеств, замкнутых относительно объединений (то есть антиматроида), можно рассматривать как аналог Теорема Биркгофа о представлении при котором любая конечная дистрибутивная решетка имеет представление в виде семейства множеств, замкнутых относительно объединений и пересечений.

Сверхрешаемые антиматроиды

Мотивировано проблемой определения частичных порядков на элементах Группа Кокстера, Армстронг (2007) изучали антиматроиды, которые также являются сверхразрешимыми решетками. Сверхразрешимый антиматроид определяется полностью заказанный набор элементов и семейство наборов этих элементов. В семье обязательно должен быть пустой набор. Кроме того, он должен иметь свойство, что если два набора А и B принадлежат семье, теоретико-множественная разница B \ А непусто, и Икс наименьший элемент B \ А, тогда А ∪ {Икс} тоже принадлежит семье. Как отмечает Армстронг, любое семейство наборов этого типа образует антиматроида. Армстронг также дает теоретико-решеточную характеристику антиматроидов, которые может образовывать эта конструкция.

Операция соединения и выпуклый размер

Если А и B являются двумя антиматроидами, оба описываются как семейство множеств, и если максимальные множества в А и B равны, мы можем сформировать еще один антиматроид, присоединиться из А и B, следующим образом:

Эта операция отличается от операции объединения, рассматриваемой в теоретико-решеточных характеристиках антиматроидов: она объединяет два антиматроида для образования другого антиматроида, а не объединяет два набора в антиматроиде для формирования другого набора. Семейство всех антиматроидов, которые имеют заданное максимальное значение. набор формирует полурешетка с этой операцией соединения.

Соединения тесно связаны с операцией закрытия, которая сопоставляет формальные языки с антиматроидами, где закрытие языка L является пересечением всех антиматроидов, содержащих L как подъязык. Это замыкание, по возможности, устанавливает объединение префиксов строк в L. В терминах этой операции замыкания соединение - это закрытие объединения языков А и B.

Каждый антиматроид может быть представлен как соединение семейства цепных антиматроидов или, что эквивалентно, как замыкание набора основных слов; то выпуклый размер антиматроида А - минимальное количество цепных антиматроидов (или эквивалентно минимальное количество основных слов) в таком представлении. Если F семейство цепных антиматроидов, все основные слова которого принадлежат А, тогда F генерирует А тогда и только тогда, когда допустимые наборы F включить все пути А. Пути А принадлежащий к одноцепочечному антиматроиду, должен образовывать цепь в пути посета А, поэтому выпуклый размер антиматроида равен минимальному количеству цепей, необходимых для покрытия пути poset, что Теорема Дилворта равна ширине пути poset.[10]

Если у кого-то есть представление об антиматроиде как об замыкании набора d базовые слова, то это представление может быть использовано для отображения возможных наборов антиматроида в d-мерное евклидово пространство: назначьте одну координату для каждого основного слова ш, и сделаем значение координаты допустимого набора S быть длиной самого длинного префикса ш это подмножество S. С этим вложением S это подмножество Т тогда и только тогда, когда координаты для S все меньше или равны соответствующим координатам Т. Следовательно размер заказа порядка включения допустимых множеств не более чем равна выпуклой размерности антиматроида.[11] Однако в целом эти два измерения могут сильно отличаться: существуют антиматроиды с размерностью третьего порядка, но с произвольно большой выпуклой размерностью.

Перечисление

Число возможных антиматроидов в наборе элементов быстро растет вместе с количеством элементов в наборе. Для наборов из одного, двух, трех и т.д. элементов количество различных антиматроидов равно

1, 3, 22, 485, 59386, 133059751, ... (последовательность A119770 в OEIS ).

Приложения

Как приоритетность, так и время выпуска в стандарте обозначения для теоретических задач планирования может быть смоделирован антиматроидами. Бойд и Фейгл (1990) использовать антиматроидов, чтобы обобщить жадный алгоритм из Юджин Лоулер для оптимального решения однопроцессорных задач планирования с ограничениями приоритета, цель которых состоит в том, чтобы минимизировать максимальные штрафы, понесенные за позднее планирование задачи.

Глассерман и Яо (1994) использовать антиматроидов для моделирования порядка событий в дискретное моделирование событий системы.

Пармар (2003) использует антиматроидов для моделирования прогресса в достижении цели в искусственный интеллект планирование проблемы.

В Теория оптимальности, грамматики логически эквивалентны антиматроидам (Торговец и Riggle (2016) ).

В математическая психология, антиматроиды использовались для описания возможные состояния знания человека-ученика. Каждый элемент антиматроида представляет собой концепцию, которую должен понять учащийся, или класс проблем, которые он или она может правильно решить, а наборы элементов, которые образуют антиматроид, представляют возможные наборы концепций, которые могут быть решены. понимает один человек. Аксиомы, определяющие антиматроид, можно неформально сформулировать как утверждение, что изучение одной концепции никогда не может помешать учащемуся изучить другую концепцию, и что любое возможное состояние знаний может быть достигнуто путем изучения одной концепции за раз. Задача системы оценки знаний состоит в том, чтобы вывести набор понятий, известных данному учащемуся, путем анализа его или ее ответов на небольшой и хорошо подобранный набор проблем. В этом контексте антиматроидов также называют «пространствами обучения» и «пространствами хорошо оцененных знаний».[12]

Заметки

  1. ^ Две ранние ссылки Эдельман (1980) и Джеймисон (1980); Джемисон был первым, кто использовал термин «антиматроид». Монжарде (1985) исследует историю повторного открытия антиматроидов.
  2. ^ Корте и др., Теорема 1.4.
  3. ^ а б c d Гордон (1997) описывает несколько результатов, относящихся к антиматроидам этого типа, но эти антиматроиды упоминались ранее, например Автор: Korte et al. Chandran et al. (2003) используют связь с антиматроидами как часть алгоритма для эффективного перечисления всех порядков идеального исключения данного хордального графа.
  4. ^ Кашивабара, Накамура и Окамото (2005).
  5. ^ Корте и др., Теорема 1.1.
  6. ^ Фарбер и Джеймисон (1986).
  7. ^ Адаричева, Горбунов и Туманов (2003), Теоремы 1.7 и 1.9; Армстронг (2007), Теорема 2.7.
  8. ^ Эдельман (1980), Теорема 3.3; Армстронг (2007), Теорема 2.8.
  9. ^ Монжарде (1985) приписывает двойную форму этой характеристики нескольким работам С. П. Аванна 1960-х годов.
  10. ^ Эдельман и Сакс (1988); Корте и др., Теорема 6.9.
  11. ^ Корте и др., Следствие 6.10.
  12. ^ Дуаньон и Фальмань (1999).

использованная литература

  • Адаричева, К. В .; Горбунов, В. А .; Туманов, В. И. (2003), "Джойн-полудистрибутивные решетки и выпуклые геометрии", Успехи в математике, 173 (1): 1–49, Дои:10.1016 / S0001-8708 (02) 00011-7.
  • Армстронг, Дрю (2007), Порядок сортировки в группе Кокстера, arXiv:0712.1047, Bibcode:2007arXiv0712.1047A.
  • Биркофф, Гарретт; Беннетт, М. К. (1985), «Решетка выпуклости чугуна», порядок, 2 (3): 223–242, Дои:10.1007 / BF00333128 (неактивно 11.11.2020)CS1 maint: DOI неактивен по состоянию на ноябрь 2020 г. (ссылка на сайт).
  • Бьёрнер, Андерс; Циглер, Гюнтер М. (1992), «Введение в гридоиды», в Уайт, Нил (ред.), Приложения Matroid, Энциклопедия математики и ее приложений, 40, Кембридж: Издательство Кембриджского университета, стр.284–357, Дои:10.1017 / CBO9780511662041.009, ISBN  0-521-38165-7, Г-Н  1165537CS1 maint: ref = harv (ссылка на сайт)
  • Бойд, Э. Эндрю; Файгл, Ульрих (1990), "Алгоритмическая характеристика антиматроидов", Дискретная прикладная математика, 28 (3): 197–205, Дои:10.1016 / 0166-218X (90) 90002-Т, HDL:1911/101636.
  • Chandran, L.S .; Ibarra, L .; Руски, Ф.; Савада, Дж. (2003), «Создание и описание идеальных порядков исключения хордального графа» (PDF), Теоретическая информатика, 307 (2): 303–317, Дои:10.1016 / S0304-3975 (03) 00221-4
  • Дилворт, Роберт П. (1940), «Решетки с единственными неприводимыми разложениями», Анналы математики, 41 (4): 771–777, Дои:10.2307/1968857, JSTOR  1968857.
  • Дуаньон, Жан-Поль; Фальмань, Жан-Клод (1999), Пространства знаний, Springer-Verlag, ISBN  3-540-64501-2.
  • Эдельман, Пол Х. (1980), "Встречно-распределительные решетки и анти-обменное замыкание", Универсальная алгебра, 10 (1): 290–299, Дои:10.1007 / BF02482912, S2CID  120403229.
  • Эдельман, Пол Х .; Сакс, Майкл Э. (1988), "Комбинаторное представление и выпуклая размерность выпуклых геометрий", порядок, 5 (1): 23–32, Дои:10.1007 / BF00143895, S2CID  119826035.
  • Фарбер, Мартин; Джеймисон, Роберт Э. (1986), "Выпуклость в графах и гиперграфах", Журнал SIAM по алгебраическим и дискретным методам, 7 (3): 433–444, Дои:10.1137/0607049, HDL:10338.dmlcz / 127659, Г-Н  0844046.
  • Глассерман, Пол; Яо, Дэвид Д. (1994), Монотонная структура в дискретных событийных системах., Серия Wiley по вероятности и статистике, Wiley Interscience, ISBN  978-0-471-58041-6.
  • Гордон, Гэри (1997), "β-инвариант для гридоидов и антиматроидов", Электронный журнал комбинаторики, 4 (1): Исследовательская статья 13, Дои:10.37236/1298, Г-Н  1445628.
  • Джеймисон, Роберт (1980), "Copoints in antimatroids", Труды одиннадцатой Юго-Восточной конференции по комбинаторике, теории графов и вычислениям (Флоридский Атлантический университет, Бока-Ратон, Флорида, 1980), Vol. II, Congressus Numerantium, 29, стр. 535–544, Г-Н  0608454.
  • Кашивабара, Кенджи; Накамура, Масатака; Окамото, Йошио (2005), "Теорема аффинного представления для абстрактных выпуклых геометрий", Вычислительная геометрия, 30 (2): 129–144, CiteSeerX  10.1.1.14.4965, Дои:10.1016 / j.comgeo.2004.05.001, Г-Н  2107032.
  • Корте, Бернхард; Ловас, Ласло; Шредер, Райнер (1991), Гридоиды, Springer-Verlag, стр. 19–43, ISBN  3-540-18190-3.