Галерея сравнения алгоритмов масштабирования изображений - Comparison gallery of image scaling algorithms

В этой галерее представлены результаты многочисленных масштабирование изображения алгоритмы.

Методы масштабирования

Размер изображения можно изменить несколькими способами. Рассмотрите возможность изменения размера фотографии 160x160 пикселей до следующей миниатюры 40x40 пикселей, а затем масштабирования миниатюры до изображения 160x160 пикселей. Также подумайте об увеличении вдвое размера следующего изображения, содержащего текст.

Изображения с низким разрешением
ЭскизТекст
Миниатюрное изображениеУменьшенное изображение исходного изображения 40x40 пикселей
Сравнение методов масштабирования
Исходное фотоУвеличенное изображениеУвеличенный текстАлгоритм и описание
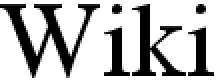Ссылка на миниатюру 160 × 160Интерполяция ближайшего соседаИнтерполяция ближайшего соседа

Интерполяция ближайшего соседа

Один из более простых способов увеличения размера, замена каждого пикселя на несколько пикселей того же цвета. Полученное изображение больше оригинала и сохраняет все исходные детали, но имеет (возможно, нежелательное) неровность. Например, диагональные линии буквы «W» теперь показывают форму «лестницы», характерную для интерполяции ближайшего соседа. Другие методы масштабирования, приведенные ниже, лучше сохраняют плавные контуры на изображении.

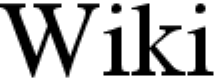Ссылка на миниатюру 160 × 160Билинейная интерполяцияЛинейная интерполяция

Билинейная интерполяция

Линейная (или билинейная в двух измерениях) интерполяция обычно хороша для изменения размера изображения, но вызывает нежелательное смягчение деталей и все же может быть несколько неровной.

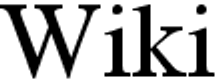Ссылка на миниатюру 160 × 160Бикубическая интерполяцияКубическая интерполяция

Бикубическая интерполяция

Лучшие методы масштабирования включают бикубическая интерполяция, Передискретизация Ланцоша и Фильтры Митчелла-Нетравали.

Ссылка на миниатюру 160 × 160Интерполяция на основе ФурьеИнтерполяция на основе Фурье + насыщение

Фурье интерполяция на основе

Простая интерполяция на основе Фурье, основанная на заполнении частотная область с нулевыми компонентами (подход на основе гладкого окна уменьшит звон ). Помимо хорошей сохранности деталей, следует отметить звон и циркулярное растекание содержимого от левого края к правому (и наоборот).

Ссылка на миниатюру 160 × 16040 на 40 уменьшенное изображение 'Green Sea Shell' (x4 DCCI) .pngВики dcci 2x.png

Направленная на кромку интерполяция

Алгоритмы направленной на края интерполяции направлены на сохранение краев изображения после масштабирования, в отличие от других алгоритмов, которые могут создавать ступенчатые артефакты вокруг диагональных линий или кривых. Примеры алгоритмов для этой задачи включают: Новая интерполяция, направленная на край (NEDI),[1][2] Интерполяция изображений по краям (EGGI),[3] Итеративная интерполяция на основе кривизны (ICBI),[4] и Направленная интерполяция кубической свертки (DCCI).[5] Исследование показало, что у DCCI лучшие результаты в PSNR и SSIM на серии тестовых изображений.[6]

Ссылка на миниатюру 160 × 160масштабирование hq4xмасштабирование hq2x

Алгоритмы масштабирования пиксельной графики

Для увеличения компьютерной графики с низким разрешением и небольшим количеством цветов (обычно от 2 до 256 цветов) лучшие результаты будут достигнуты с помощью алгоритмов масштабирования пиксельной графики, таких как hqx. Они создают острые края и поддерживают высокий уровень детализации.

Ссылка на миниатюру 160 × 160Векторизация до 48 цветов (Inkscape)Векторизация

Трассировка изображений

Векторизация сначала создает не зависящее от разрешения векторное представление масштабируемой графики. Затем версия, не зависящая от разрешения, визуализируется как растровое изображение с желаемым разрешением. Этот метод используется Adobe Illustrator Живая трассировка, Inkscape, и несколько недавних статей.[7]Масштабируемая векторная графика хорошо подходят для простых геометрических изображений, тогда как фотографии плохо справляются с векторизацией из-за их сложности.

Ссылка на миниатюру 160 × 160EDSRwaifu2x

Глубокий сверточные нейронные сети

С помощью машинное обучение, убедительные детали генерируются как наилучшие предположения путем изучения общих закономерностей из набор обучающих данных. Результат апскейлинга иногда описывается как галлюцинация потому что введенная информация может не соответствовать содержанию источника. Методы расширенной глубокой остаточной сети (EDSR) были разработаны путем оптимизации обычных остаточная нейронная сеть архитектура.[8] Программы, использующие этот метод, включают waifu2x, Увеличение и усиление нейронов.

Ссылка на миниатюру 160 × 160ESRGAN

Глубокий сверточные нейронные сети используя перцептивный потеря

Разработано на основе сверхвысокого разрешения порождающая состязательная сеть (SRGAN) метод,[9] улучшенный СРГАН (ESRGAN)[10] представляет собой постепенную настройку той же основы генеративной противоборствующей сети. Оба метода основаны на восприятии. функция потерь[11] для оценки итераций обучения.

Рекомендации

  1. ^ "Интерполяция с краю". Получено 19 февраля 2016.
  2. ^ Синь Ли; Майкл Т. Орчард. "НОВАЯ НАПРАВЛЕННАЯ ИНТЕРПОЛЯЦИЯ" (PDF). 2000 Международная конференция IEEE по обработке изображений: 311. Архивировано с оригинал (PDF) на 2016-02-14. Получено 2016-07-03.
  3. ^ Zhang, D .; Сяолинь Ву (2006). «Алгоритм интерполяции изображений с контролем по краям с помощью направленной фильтрации и объединения данных». IEEE Transactions по обработке изображений. 15 (8): 2226–38. Bibcode:2006ITIP ... 15.2226Z. Дои:10.1109 / TIP.2006.877407. PMID  16900678. S2CID  9760560.
  4. ^ К. Сридхар Редди; Доктор К. Рама Линга Редди (декабрь 2013 г.). «Увеличение изображения на основе методов интерполяции» (PDF). Международный журнал перспективных исследований в области компьютерной и коммуникационной техники. 2 (12): 4631.
  5. ^ Дэнвэнь Чжоу; Сяолиу Шэнь. «Масштабирование изображения с использованием направленной кубической интерполяции свертки». Получено 13 сентября 2015.
  6. ^ Шаод Ю; Ронгмао Ли; Руи Чжан; Mou An; Шибин Ву; Яоцинь Се (2013). «Оценка эффективности методов краевой интерполяции для изображений без шума». arXiv:1303.6455 [cs.CV ].
  7. ^ Йоханнес Копф и Дани Лищински (2011). «Депикселизация пиксель-арта». Транзакции ACM на графике. 30 (4): 99:1–99:8. Дои:10.1145/2010324.1964994. Архивировано из оригинал на 2015-09-01. Получено 24 октября 2012.
  8. ^ Лим, Пчела; Сын, Санхьюн; Ким, Хивон; Нет, Сынджун; Кён Му Ли (2017). «Расширенные глубокие остаточные сети для сверхвысокого разрешения одиночного изображения». arXiv:1707.02921 [cs.CV ].
  9. ^ «Генеративная состязательная сеть и GAN со сверхвысоким разрешением (SRGAN)». Получено 26 августа 2020.
  10. ^ Ван, Синтао; Ю, Кэ; Ву, Шисян; Гу, Джинджин; Лю, Ихао; Донг, Чао; Чен Чейнджер Лой; Цяо, Ю; Тан, Сяоу (2018). «ESRGAN: Расширенные состязательные сети со сверхвысоким разрешением». arXiv:1809.00219 [cs.CV ].
  11. ^ «Функции потери восприятия». Получено 26 августа 2020.