График дезарга - Desargues graph
| График дезарга | |
|---|---|
 | |
| Названный в честь | Жерар Дезарг |
| Вершины | 20 |
| Края | 30 |
| Радиус | 5 |
| Диаметр | 5 |
| Обхват | 6 |
| Автоморфизмы | 240 (S5× Z/2Z) |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Род | 2 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Свойства | Кубический Дистанционно-регулярный Гамильтониан Двудольный Симметричный |
| Таблица графиков и параметров | |
в математический поле теория графов, то График дезарга это дистанционно-переходный кубический граф с 20 вершинами и 30 ребрами.[1] Он назван в честь Жирар Дезарг, возникает из нескольких различных комбинаторных конструкций, имеет высокий уровень симметрии, является единственным известным непланарный кубический частичный куб, и был применен в химических базах данных.
Название «граф Дезарга» также использовалось для обозначения десятивершинного графа, дополнения Граф Петерсена, который также может быть сформирован как двудольная половина 20-вершинного графа Дезарга.[2]
Конструкции
Есть несколько разных способов построения графа Дезарга:
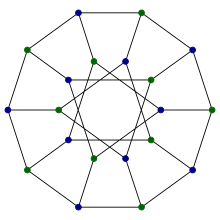
- Это обобщенный граф Петерсена г(10, 3). Чтобы сформировать граф Дезарга таким образом, соедините десять вершин в правильный десятиугольник, а остальные десять вершин соединить в десятиугольную звезду, которая соединяет пары вершин на расстоянии три во втором десятиугольнике. Граф Дезарга состоит из 20 ребер этих двух многоугольников вместе с дополнительными 10 ребрами, соединяющими точки одного десятиугольника с соответствующими точками другого.
- Это Граф Леви из Конфигурация дезарга. Эта конфигурация состоит из десяти точек и десяти строк, описывающих два перспективные треугольники, их центр перспективы и их ось перспективы. Граф Дезарга имеет по одной вершине для каждой точки, по одной вершине для каждой линии и по одному ребру для каждой пары инцидентных точек и линий. Теорема дезарга, названный в честь французского математика 17 века Жерар Дезарг, описывает набор точек и линий, образующих эту конфигурацию, а конфигурация и граф получили свое название от него.
- Это двусторонняя двойная обложка из Граф Петерсена, образованный заменой каждой вершины графа Петерсена парой вершин и каждого ребра графа Петерсена парой скрещенных ребер.
- Это двудольный граф Кнезера ЧАС5,2. Его вершины могут быть помечены десятью двухэлементными подмножествами и десятью трехэлементными подмножествами пятиэлементного набора с ребром, соединяющим две вершины, когда одно из соответствующих наборов является подмножеством другого. Эквивалентно граф Дезарга - это индуцированный подграф 5-мерного гиперкуба, определяемого вершинами веса 2 и веса 3.
- Граф Дезарга имеет вид Гамильтониан и может быть построен из Обозначение LCF: [5,−5,9,−9]5. Так как Erds предположил, что при положительном k подграф 2k + 1-мерного гиперкуба, индуцированный вершинами веса k и k + 1, является гамильтоновым, гамильтоничность графа Дезарга неудивительна. (Из более сильной гипотезы Ловаса также следует, что, за исключением нескольких известных контрпримеров, все вершинно-транзитивные графы имеют гамильтоновы циклы.)
Алгебраические свойства
Граф Дезарга - это симметричный граф: он имеет симметрии, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Его группа симметрии имеет порядок 240 и изоморфна произведению симметричная группа на 5 баллов с группой порядка 2.
Это представление продукта группы симметрии можно интерпретировать в терминах конструкций графа Дезарга: симметрическая группа по пяти точкам - это группа симметрии конфигурации Дезарга, а подгруппа порядка 2 меняет местами роли вершин, представляющих точки конфигурации Дезарга и вершины, представляющие линии. В качестве альтернативы, в терминах двудольного графа Кнезера, симметрическая группа на пяти точках действует отдельно на двухэлементные и трехэлементные подмножества пяти точек, а дополнение подмножеств образует группу второго порядка, которая преобразует один тип подмножества в другой. Симметрическая группа на пяти точках также является группой симметрии графа Петерсена, а подгруппа порядка 2 меняет местами вершины внутри каждой пары вершин, образованных в конструкции двойного покрытия.
Обобщенный граф Петерсена г(п, k) вершинно-транзитивно тогда и только тогда, когда п = 10 и k = 2 или если k2 ≡ ± 1 (мод.п) и является реберно-транзитивным только в следующих семи случаях: (п, k) = (4, 1), (5, 2), (8, 3), (10, 2), (10, 3), (12, 5), (24, 5).[3] Итак, граф Дезарга - один из семи симметричных обобщенных графов Петерсена. Среди этих семи графиков есть кубический график г(4, 1), Граф Петерсена г(5, 2), График Мёбиуса – Кантора г(8, 3), додекаэдрический граф г(10, 2) и Науру график г(12, 5).
В характеристический многочлен графа Дезарга есть
Следовательно, граф Дезарга является интегральный график: его спектр полностью состоит из целых чисел.
Приложения
В химия, граф Дезарга известен как Граф Дезарга – Леви; он используется для организации систем стереоизомеры из 5-лиганд соединения. В этом приложении тридцать ребер графа соответствуют псевдовращения лигандов.[4][5]
Другие свойства
Граф Дезарга имеет номер прямолинейного перехода 6, и является наименьшим кубическим графом с этим числом пересечения (последовательность A110507 в OEIS ). Это единственная известная неплоская кубическая частичный куб.[6]
Граф Дезарга имеет хроматическое число 2, хроматический индекс 3, радиус 5, диаметр 5 и обхват 6. Это также 3-вершинно-связанный и 3-реберный Гамильтонов граф. Она имеет толщина книги 3 и номер очереди 2.[7]
Все кубический дистанционно регулярные графы известны.[8] Граф Дезарга - один из 13 таких графов.
Граф Дезарга может быть вложен как само-Петри двойной обычная карта в неориентируемом многообразии рода 6 с декагональными гранями.
Галерея

График Дезарга раскрашен для выделения различных циклов.

В хроматический индекс графа Дезарга равно 3.

В хроматическое число графа Дезарга равно 2.
использованная литература
- ^ Вайсштейн, Эрик В. «График Дезарга». MathWorld.
- ^ Кагно, И. Н. (1947), "Графы Дезарга и Паппа и их группы", Американский журнал математики, Издательство Университета Джона Хопкинса, 69 (4): 859–863, Дои:10.2307/2371806, JSTOR 2371806.
- ^ Фрухт, Р.; Graver, J. E .; Уоткинс, М. Э. (1971), "Группы обобщенных графов Петерсена", Труды Кембриджское философское общество, 70 (02): 211–218, Дои:10.1017 / S0305004100049811.
- ^ Балабан, А. Т .; Fǎrcaşiu, D .; Bǎnic, R. (1966), "Графики множественных 1,2-сдвигов в ионах карбония и родственных системах", Преподобный Рум. Чим., 11: 1205
- ^ Мислоу, Курт (1970), «Роль псевдовращения в стереохимии реакций нуклеофильного замещения», Соотв. Chem. Res., 3 (10): 321–331, Дои:10.1021 / ar50034a001
- ^ Клавжар, Санди; Липовец, Аленка (2003), "Частичные кубы как графы подразделений и как обобщенные графы Петерсена", Дискретная математика, 263: 157–165, Дои:10.1016 / S0012-365X (02) 00575-7
- ^ Вольц, Джессика, Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
- ^ Брауэр, А.Э.; Коэн, А. М .; и Ноймайер А. Дистанционно регулярные графы. Нью-Йорк: Springer-Verlag, 1989.




