Граф Леви - Levi graph
| Граф Леви | |
|---|---|
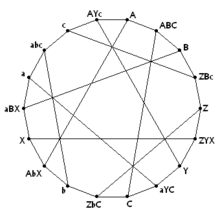 В График Паппа, граф Леви с 18 вершинами, образованный Конфигурация Pappus. Вершины, помеченные одиночными буквами, соответствуют точкам в конфигурации; вершины, помеченные тремя буквами, соответствуют линиям, проходящим через три точки. | |
| Обхват | ≥ 6 |
| Таблица графиков и параметров | |
В комбинаторная математика, а Граф Леви или график заболеваемости это двудольный граф связанный с структура заболеваемости.[1][2] Из набора точек и линий в геометрия падения или проективная конфигурация, мы формируем граф с одной вершиной на точку, одной вершиной на линию и ребром для каждого пересечения между точкой и прямой. Они названы в честь Фридрих Вильгельм Леви, писавший о них в 1942 году.[1][3]
Граф Леви системы точек и линий обычно имеет обхват минимум шесть: Любые 4-циклы будет соответствовать двум линиям через одни и те же две точки. И наоборот, любой двудольный граф с обхватом не менее шести можно рассматривать как граф Леви абстрактной структуры инцидентности.[1] Графы Леви конфигураций двурегулярный, и каждый бирегулярный граф с обхватом не менее шести можно рассматривать как граф Леви абстрактной конфигурации.[4]
Графы Леви также могут быть определены для других типов структуры инцидентов, таких как инциденты между точками и плоскостями в Евклидово пространство. Для каждого графа Леви существует эквивалент гиперграф, и наоборот.
Примеры
- В График дезарга является графом Леви Конфигурация дезарга, состоящий из 10 точек и 10 строк. На каждой линии по 3 точки, и через каждую точку проходят 3 линии. График Дезарга также можно рассматривать как обобщенный граф Петерсена G (10,3) или двудольный граф Кнезера с параметрами 5,2. Он 3-регулярный с 20 вершинами.
- В График Хивуда является графом Леви Самолет Фано. Он также известен как (3,6) -клетка, и является 3-регулярным с 14 вершинами.
- В График Мёбиуса – Кантора является графом Леви Конфигурация Мебиуса – Кантора, система из 8 точек и 8 прямых, которые не могут быть реализованы прямыми линиями на евклидовой плоскости. Он 3-регулярный с 16 вершинами.
- В График Паппа является графом Леви Конфигурация Pappus, состоящий из 9 точек и 9 строк. Как и в конфигурации Дезарга, на каждой линии есть 3 точки и через каждую точку проходят 3 линии. Он 3-регулярный с 18 вершинами.
- В Серый график является графом Леви конфигурации, которая может быть реализована в как сетка из 27 точек и 27 ортогональных линий, проходящих через них.
- В Тутте восемь клеток является графом Леви Конфигурация Кремона – Ричмонд. Она также известна как (3,8) -клетка и является 3-правильной с 30 вершинами.
- Четырехмерный граф гиперкуба является графом Леви Конфигурация Мебиуса образованный точками и плоскостями двух взаимно инцидентных тетраэдров.
- В Любляна график на 112 вершинах - граф Леви конфигурации Любляны.[5]
Рекомендации
- ^ а б c Грюнбаум, Бранко (2006), «Конфигурации точек и линий», Наследие Кокстера, Провиденс, Род-Айленд: Американское математическое общество, стр. 179–225, Г-Н 2209028. См. В частности п. 181.
- ^ Polster, Burkard (1998), Геометрическая книга с картинками, Universitext, New York: Springer-Verlag, p. 5, Дои:10.1007/978-1-4419-8526-2, ISBN 0-387-98437-2, Г-Н 1640615.
- ^ Леви, Ф. В. (1942), Конечные геометрические системы, Калькутта: Калькуттский университет, Г-Н 0006834.
- ^ Gropp, Harald (2007), «Конфигурации VI.7», в Colbourn, Charles J .; Диниц, Джеффри Х. (ред.), Справочник комбинаторных планов, Дискретная математика и ее приложения (Бока-Ратон) (второе изд.), Chapman & Hall / CRC, Бока-Ратон, Флорида, стр. 353–355..
- ^ Кондер, Марстон; Малнич, Александр; Марушич, Драган; Писанский, Томаж; Поточник, Примож (2002), Люблянский график (PDF), Препринт МВФМ 40-845, факультет математики Люблянского университета.



