Додекагональная антипризма - Википедия - Dodecagonal antiprism

Равномерная двенадцатигранная антипризма

Тип	Призматический однородный многогранник
Элементы	F = 26, E = 48 V = 24 (χ = 2)
Лица по сторонам	24{3}+2{12}
Символ Шлефли	с {2,24} sr {2,12}
Символ Wythoff	\| 2 2 12
Диаграмма Кокстера
Группа симметрии	D_12d, [2⁺, 24], (2 * 12), порядок 48
Группа вращения	D₁₂, [12,2]⁺, (12.2.2), порядок 24
Рекомендации	U_{77 (j)}
Двойной	Додекагональный трапецииэдр
Характеристики	выпуклый
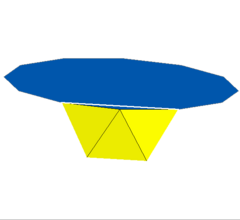Фигура вершины 3.3.3.12

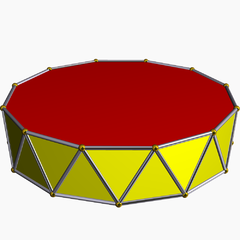
В геометрия, то двенадцатигранная антипризма является десятым в бесконечном наборе антипризмы образованный четной последовательностью сторон треугольника, закрытых двумя крышками многоугольника.

Антипризмы похожи на призмы за исключением того, что основания скручены относительно друг друга, а боковые грани представляют собой треугольники, а не четырехугольники.

В случае обычной 12-гранной основы обычно рассматривают случай, когда ее копия закручена на угол 180 ° /п. Дополнительная регулярность достигается за счет того, что линия, соединяющая центры основания, перпендикулярна плоскостям основания, что делает ее прямой. правая антипризма. Как лица, он имеет два п-гональный базы и, соединяя эти базы, 2п равнобедренные треугольники.

Если все лица правильные, это полуправильный многогранник.

Смотрите также

Семья униформы п-гональный антипризмы v т е
Изображение многогранника												...	Апейрогональная антипризма
Сферическое мозаичное изображение												Плоское мозаичное изображение
Конфигурация вершины п.3.3.3	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3