Теория Франк-Каменецкого - Википедия - Frank-Kamenetskii theory

В горение, Теория Франк-Каменецкого объясняет тепловой взрыв однородной смеси реагентов, хранящейся в закрытом сосуде с постоянной температурой стенок. Назван в честь русского ученого. Давид А. Франк-Каменецкий, который вместе с Николай Семенов разработал теорию в 1930-х гг.^[1][2][3][4]

Описание проблемы^{[5][6][7][8][9]}

Рассмотрим сосуд, в котором поддерживается постоянная температура. ${ displaystyle T_ {o}}$, содержащий гомогенную реакционную смесь. Пусть характерный размер судна равен ${ displaystyle a}$. Поскольку смесь однородна, плотность ${ displaystyle rho}$ постоянно. В начальный период зажигание, расход концентрации реагента незначителен (см. ${ displaystyle t_ {f}}$ и ${ displaystyle t_ {e}}$ ниже), поэтому взрыв регулируется только уравнением энергии. Предполагая одноэтапную глобальную реакцию ${ displaystyle { text {топливо}} + { text {окислитель}} rightarrow { text {products}} + q}$, куда ${ displaystyle q}$ - количество тепла, выделяемого на единицу массы израсходованного топлива, а скорость реакции определяется Закон Аррениуса, уравнение энергии принимает вид

${ Displaystyle rho c_ {v} { frac { partial T} { partial t}} = lambda nabla ^ {2} T + q rho BY_ {Fo} e ^ {- E / (RT) }}$

куда

• ${ displaystyle T}$ это температура смеси
• ${ displaystyle c_ {v}}$ это удельная теплоемкость при постоянной громкости
• ${ displaystyle lambda}$ это теплопроводность
• ${ displaystyle B}$ это предэкспоненциальный множитель с размерностью одного с течением времени
• ${ displaystyle Y_ {Fo}}$ это начальное топливо массовая доля
• ${ displaystyle E}$ это энергия активации
• ${ displaystyle R}$ это универсальная газовая постоянная

Безразмерность

Безразмерная энергия активации ${ displaystyle beta}$ и параметр тепловыделения ${ displaystyle gamma}$ находятся

${ displaystyle beta = { frac {E} {RT_ {o}}}, quad gamma = { frac {qY_ {Fo}} {c_ {v} T_ {o}}}}$

Характерное время теплопроводности по емкости составляет ${ displaystyle t_ {c} = rho c_ {v} a ^ {2} / lambda}$, характерное время расхода топлива составляет ${ displaystyle t_ {f} = left (Be ^ {- beta} right) ^ {- 1}}$ а характерное время взрыва / возгорания ${ displaystyle t_ {e} = left ( beta gamma Be ^ {- beta} right) ^ {- 1}}$. Следует отметить, что в процессе горения обычно ${ displaystyle gamma приблизительно 6 {-} 8, beta приблизительно 30 {-} 100}$ так что ${ Displaystyle бета гамма gg 1}$. Следовательно, ${ Displaystyle т_ {е} = бета гамма т_ {е} gg 1}$т. е. топливо расходуется гораздо дольше, чем время воспламенения, расход топлива существенно незначителен для изучения воспламенения / взрыва. По этой причине предполагается, что концентрация топлива такая же, как и исходная концентрация топлива. ${ displaystyle Y_ {Fo}}$. Безразмерные масштабы

${ displaystyle tau = { frac {t} {t_ {e}}}, quad theta = { frac { beta (T-T_ {o})} {T_ {o}}}, quad eta ^ {j} = { frac {r ^ {j}} {a}}, quad delta = { frac {t_ {c}} {t_ {e}}}}$

куда ${ displaystyle delta}$ это Число Дамкёлера и ${ displaystyle r}$ - пространственная координата с началом в центре, ${ displaystyle j = 0}$ для плоской плиты, ${ displaystyle j = 1}$ для цилиндрического сосуда и ${ displaystyle j = 2}$ для сферического сосуда. В этом масштабе уравнение принимает вид

${ displaystyle { frac { partial theta} { partial tau}} = { frac {1} { delta}} { frac {1} { eta ^ {j}}} { frac { partial} { partial eta}} left ( eta ^ {j} { frac { partial theta} { partial eta}} right) + e ^ { theta / (1+ theta / beta)}}$

С ${ displaystyle beta gg 1}$, экспоненциальный член можно линеаризовать ${ Displaystyle е ^ { тета / (1+ тета / бета)} приблизительно е ^ { тета}}$, следовательно

${ displaystyle { frac { partial theta} { partial tau}} = { frac {1} { delta}} { frac {1} { eta ^ {j}}} { frac { partial} { partial eta}} left ( eta ^ {j} { frac { partial theta} { partial eta}} right) + e ^ { theta}}$

Теория Семенова

Перед Франк-Каменецкий, его научный руководитель Николай Семенов (или Семенов) предложил теорию теплового взрыва с простой моделью, т.е. он предположил линейную функцию для процесса теплопроводности вместо Лапласиан оператор. Уравнение Семенова читается как

${ displaystyle { frac { partial theta} { partial tau}} = e ^ { theta} - { frac { theta} { delta}}, quad theta (0) = 0}$

За ${ Displaystyle е ^ {- 1} < дельта < infty}$, система взорвется, поскольку экспоненциальный член доминирует. За ${ Displaystyle 0 < дельта <е ^ {- 1}}$, система переходит в устойчивое состояние, система не взрывается. В частности, Семенов нашел критическое Число Дамкёлера, который называется Параметр Франк-Каменецкого ${ displaystyle delta _ {c} = e ^ {- 1}}$(куда ${ Displaystyle theta = 1}$) как критическая точка, в которой система переходит из устойчивого состояния во взрывоопасное. За ${ displaystyle delta gg 1}$, решение

${ displaystyle { frac { partial theta} { partial tau}} = e ^ { theta}, quad Rightarrow quad theta = ln left ({ frac {1} {1- tau}} right)}$

Вовремя ${ Displaystyle тау = 1}$, система взорвется. Это время также называют период адиабатической индукции поскольку теплопроводность здесь незначительна.

Теория стационарного состояния Франк-Каменецкого^[10][11]

Единственный параметр, характеризующий взрыв, - это Число Дамкёлера ${ displaystyle delta}$. Когда ${ displaystyle delta}$ очень велико, время теплопроводности больше, чем время химической реакции, и система взрывается при высокой температуре, так как для теплопроводности недостаточно времени для отвода тепла. С другой стороны, когда ${ displaystyle delta}$ очень мала, время теплопроводности намного меньше, чем время химической реакции, так что все тепло, производимое химической реакцией, немедленно передается на стену, поэтому взрыва нет, оно переходит в почти устойчивое состояние, Amable Liñán придумал этот режим как режим медленного реагирования. При критическом числе Дамкелера ${ displaystyle delta _ {c}}$ система переходит из режима медленного реагирования во взрывной режим. Следовательно, ${ displaystyle delta < delta _ {c}}$, система находится в устойчивом состоянии. Вместо того, чтобы решать всю проблему, чтобы найти это ${ displaystyle delta _ {c}}$, Франк-Каменецкий решил задачу о стационарном состоянии для различных чисел Дамкелера до критического значения, за пределами которого не существует устойчивого решения. Итак, проблема, которую нужно решить,

${ displaystyle { frac {1} { eta ^ {j}}} { frac {d} {d eta}} left ( eta ^ {j} { frac {d theta} {d eta}} right) = - delta e ^ { theta}}$

с граничными условиями

${ displaystyle theta (1) = 0, quad { frac {d theta} {d eta}} _ { eta = 0} = 0}$

второе условие связано с симметрией сосуда. Вышеприведенное уравнение является частным случаем Уравнение Лиувилля – Брату – Гельфанда. в математика.

Плоское судно

Франк-Каменецкий взрыв для планарного судна

Для плоского сосуда есть точное решение. Здесь ${ displaystyle j = 0}$, тогда

${ displaystyle { frac {d ^ {2} theta} {d eta ^ {2}}} = - delta e ^ { theta}}$

Если преобразования ${ Displaystyle Theta = theta _ {m} - theta}$ и ${ displaystyle xi ^ {2} = delta e ^ { theta _ {m}} eta ^ {2}}$, куда ${ displaystyle theta _ {m}}$ это максимальная температура, которая возникает при ${ displaystyle eta = 0}$ в силу симметрии вводятся

${ displaystyle { frac {d ^ {2} Theta} {d xi ^ {2}}} = e ^ {- Theta}, quad Theta (0) = 0, quad { frac { d Theta} {d xi}} _ { xi = 0} = 0}$

После однократного интегрирования и использования второго граничного условия уравнение принимает вид

${ displaystyle { frac {d Theta} {d xi}} = { sqrt {2 (1-e ^ {- Theta})}}}$

и снова интегрируя

${ displaystyle e ^ {( theta _ {m} - theta) / 2} = cosh left ({ sqrt { frac { delta e ^ { theta _ {m}}} {2}} } eta right)}$

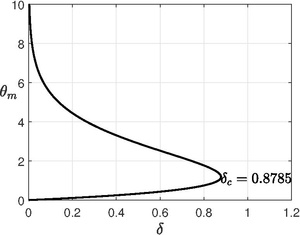
Вышеприведенное уравнение является точным решением, но ${ displaystyle theta _ {m}}$ максимальная температура неизвестна, но мы еще не использовали граничное условие стенки. Таким образом, используя граничное условие стенки ${ displaystyle theta = 0}$ в ${ displaystyle eta = 1}$, максимальная температура получается из неявного выражения,

${ displaystyle e ^ { theta _ {m} / 2} = cosh left ({ sqrt { frac { delta e ^ { theta _ {m}}} {2}}} right) quad { text {или}} quad delta = 2e ^ {- theta _ {m}} left ( cosh ^ {- 1} e ^ { theta _ {m} / 2} right) ^ {2}}$

Критический ${ displaystyle delta _ {c}}$ получается путем нахождения максимальной точки уравнения (см. рисунок), т.е. ${ displaystyle d delta / d theta _ {m} = 0}$ в ${ displaystyle delta _ {c}}$.

${ displaystyle { frac {d delta} {d theta _ {m}}} = 0, quad Rightarrow quad e ^ { theta _ {m, c} / 2} - { sqrt {e ^ { theta _ {m, c}} - 1}} ch ^ {- 1} e ^ { theta _ {m, c} / 2} = 0}$

${ displaystyle theta _ {m, c} = 1,1868, quad Rightarrow quad delta _ {c} = 0,8785}$

Таким образом, критический параметр Франка-Каменского равен ${ displaystyle delta _ {c} = 0,8785}$. Система не имеет устойчивого состояния (или взрывается) в течение ${ displaystyle delta> delta _ {c} = 0,8785}$ и для ${ displaystyle delta < delta _ {c} = 0,8785}$, система переходит в устойчивое состояние с очень медленной реакцией.

Цилиндрический сосуд

Франк-Каменецкий взрыв для цилиндрического сосуда

Для цилиндрического сосуда есть точное решение. Хотя Франк-Каменцкий использовал численное интегрирование, предполагая, что явного решения нет, Поль Л. Шамбре предоставил точное решение в 1952 году.^[12] Х. Лемке также предложил решение в несколько иной форме в 1913 г.^[13] Здесь ${ displaystyle j = 1}$, тогда

${ displaystyle { frac {1} { eta}} { frac {d} {d eta}} left ( eta { frac {d theta} {d eta}} right) = - delta e ^ { theta}}$

Если преобразования ${ displaystyle omega = eta d theta / d eta}$ и ${ Displaystyle чи = е ^ { тета} eta ^ {2}}$ представлены

${ displaystyle { frac {d omega} {d chi}} = - { frac { delta} {2+ omega}}, quad omega (0) = 0}$

Общее решение ${ displaystyle omega ^ {2} +4 omega + C = -2 delta chi}$. Но ${ displaystyle C = 0}$ из условия симметрии в центре. Записываясь обратно в исходную переменную, уравнение читается так:

${ displaystyle eta ^ {2} left ({ frac {d theta} {d eta}} right) ^ {2} +4 eta { frac {d theta} {d eta} } = - 2 delta eta ^ {2} e ^ { theta}}$

Но исходное уравнение, умноженное на ${ displaystyle 2 eta ^ {2}}$ является

${ displaystyle 2 eta ^ {2} { frac {d ^ {2} theta} {d eta ^ {2}}} + 2 eta { frac {d theta} {d eta}} = -2 delta eta ^ {2} e ^ { theta}}$

Теперь вычитание двух последних уравнений друг из друга приводит к

${ displaystyle { frac {d ^ {2} theta} {d eta ^ {2}}} - { frac {1} { eta}} { frac {d theta} {d eta} } - { frac {1} {2}} left ({ frac {d theta} {d eta}} right) ^ {2} = 0}$

Это уравнение легко решить, потому что оно включает только производные, поэтому позволяя ${ Displaystyle г ( eta) = d theta / d eta}$ преобразует уравнение

${ displaystyle { frac {dg} {d eta}} - { frac {g} { eta}} - { frac {g ^ {2}} {2}} = 0}$

Это Дифференциальное уравнение Бернулли порядка ${ displaystyle 2}$, тип Уравнение Риккати. Решение

${ displaystyle g ( eta) = { frac {d theta} {d eta}} = - { frac {4 eta} {B '+ eta ^ {2}}}}$

Интегрируя еще раз, мы имеем ${ displaystyle theta = A-2 ln (B eta ^ {2} +1)}$ куда ${ Displaystyle B = 1 / B '}$. Мы использовали уже одно граничное условие, осталось еще одно граничное условие, но с двумя константами ${ displaystyle A, B}$. Оказывается ${ displaystyle A}$ и ${ displaystyle B}$ связаны друг с другом, что получается путем подстановки указанного выше решения в исходное уравнение, мы приходим к ${ Displaystyle А = пер (8B / дельта)}$. Следовательно, решение

${ displaystyle theta = ln left [{ frac {8B / delta} {(B eta ^ {2} +1) ^ {2}}} right]}$

Теперь, если мы воспользуемся другим граничным условием ${ Displaystyle theta (1) = 0}$, получаем уравнение для ${ displaystyle B}$ в качестве ${ displaystyle delta (B + 1) ^ {2} -8B = 0}$. Максимальное значение ${ displaystyle delta}$ для которого решение возможно, когда ${ displaystyle B = 1}$, поэтому критический параметр Франка-Каменского равен ${ displaystyle delta _ {c} = 2}$. Система не имеет устойчивого состояния (или взрывается) в течение ${ displaystyle delta> delta _ {c} = 2}$ и для ${ displaystyle delta < delta _ {c} = 2}$, система переходит в устойчивое состояние с очень медленной реакцией. Максимальная температура ${ displaystyle theta _ {m}}$ происходит в ${ displaystyle eta = 0}$

${ displaystyle theta _ {m} = ln left ({ frac {8B} { delta}} right) quad { text {или}} quad delta = 8Be ^ {- theta _ {m}}}$

Для каждого значения ${ displaystyle delta}$, имеем два значения ${ displaystyle theta _ {m}}$ поскольку ${ displaystyle B}$ многозначен. Максимальная критическая температура составляет ${ displaystyle theta _ {m, c} = ln 4}$.

Сферический сосуд

Для сферического сосуда нет явного решения, поэтому Франк-Каменецкий использовали численные методы для определения критического значения. Здесь ${ displaystyle j = 2}$, тогда

${ displaystyle { frac {1} { eta ^ {2}}} { frac {d} {d eta}} left ( eta ^ {2} { frac {d theta} {d eta}} right) = - delta e ^ { theta}}$

Если преобразования ${ Displaystyle Theta = theta _ {m} - theta}$ и ${ displaystyle xi ^ {2} = delta e ^ { theta _ {m}} eta ^ {2}}$, куда ${ displaystyle theta _ {m}}$ это максимальная температура, которая возникает при ${ displaystyle eta = 0}$ в силу симметрии вводятся

${ displaystyle { frac {1} { xi ^ {2}}} { frac {d} {d xi}} left ( xi ^ {2} { frac {d Theta} {d xi}} right) = e ^ {- Theta}, quad Theta (0) = 0, quad { frac {d Theta} {d xi}} _ { xi = 0} = 0 }$

Вышеприведенное уравнение - не что иное, как Уравнение Эмдена – Чандрасекара,^[14] который появляется в астрофизика описание изотермический газовая сфера. В отличие от плоского и цилиндрического корпуса сферический сосуд имеет бесконечное множество решений для ${ displaystyle delta < delta _ {c}}$ колебаться вокруг точки ${ displaystyle delta = 2}$,^[15] вместо двух решений, как показал Израиль Гельфанд.^[16] Для объяснения взрывного поведения будет выбрана самая нижняя ветвь.

Численным решением установлено, что критический параметр Франка-Каменецкого равен ${ displaystyle delta _ {c} = 3,32}$. Система не имеет устойчивого состояния (или взрывается) в течение ${ displaystyle delta> delta _ {c} = 3,32}$ и для ${ displaystyle delta < delta _ {c} = 3.32}$, система переходит в устойчивое состояние с очень медленной реакцией. Максимальная температура ${ displaystyle theta _ {m}}$ происходит в ${ displaystyle eta = 0}$ а максимальная критическая температура составляет ${ displaystyle theta _ {m, c} = 1,61}$.

Несимметричные геометрии

Для сосудов, которые не являются симметричными относительно центра (например, прямоугольный сосуд), проблема заключается в решении нелинейного уравнение в частных производных вместо нелинейного обыкновенное дифференциальное уравнение, которые в большинстве случаев могут быть решены только численными методами. Уравнение

${ Displaystyle набла ^ {2} тета + дельта е ^ { тета} = 0}$

с граничным условием ${ displaystyle theta = 0}$ на ограничивающих поверхностях.

Приложения

Поскольку модель предполагает однородную смесь, теория хорошо применима для изучения взрывоопасного поведения твердого топлива (самовозгорание биотоплива, органических материалов, мусора и т. Д.). Это также используется для конструирования взрывчатых веществ и взломщиков огня. Теория точно предсказала критические значения для жидкостей / твердых тел с низкой проводимостью и тонкостенных контейнеров с высокой проводимостью.^[17]

Смотрите также

• Уравнение Кларка

Рекомендации

внешняя ссылка

• Проблема Франк-Каменецкого в Вольфрам решатель http://demonstrations.wolfram.com/TheFrankKamenetskiiProblem/
• Отслеживание проблемы Франк-Каменецкого в Вольфрам решатель http://demonstrations.wolfram.com/TrackingTheFrankKamenetskiiProblem/
• Планарное решение в Chebfun решатель http://www.chebfun.org/examples/ode-nonlin/BlowupFK.html