Правила голосования с наивысшим средним значением - Википедия - Highest median voting rules

Правила голосования наивысшей медианы находятся кардинальное голосование правила, где победителем является кандидат с наивысшим средним рейтингом. Поскольку в них используются рейтинги, каждый избиратель оценивает разных кандидатов по упорядоченной, числовой или устной шкале.

Различные правила наивысшей медианы различаются обработкой связей, то есть методом ранжирования кандидатов с одинаковым медианным рейтингом.

Сторонники правил наивысшей медианы утверждают, что они точно отражают мнение избирателя, что они удовлетворяют независимость от нерелевантных альтернатив и не подпадают под действие Теорема о невозможности Эрроу.^[1] Критики отмечают, что правила наивысшей медианы нарушают Критерий Кондорсе: кандидат в принципе может быть избран, даже если все избиратели, кроме одного, предпочитают другого кандидата.^[2]^[3]

Определение и обозначения

Позволять ${ Displaystyle { mathcal {C}}}$ быть набором кандидатов, ${ Displaystyle { mathcal {V}}}$ набор избирателей, и ${ Displaystyle { mathcal {G}}}$ упорядоченный конечный набор оценок (например, следующие оценки: «Очень хорошо», «Хорошо», «Средне», «Плохо»).

Для любого кандидата ${ displaystyle c in { mathcal {C}}}$ , ${ displaystyle c}$ средний рейтинг ${ displaystyle alpha _ {c} in { mathcal {G}}}$ это средний рейтинг среди рейтингов, которые ${ displaystyle c}$ получено от избирателей. Например, если есть десять избирателей и если кандидат ${ displaystyle A}$ получает три оценки "Хорошо", шесть оценок "Средне" и одну оценку "Плохо", свой средний рейтинг. ${ displaystyle alpha _ {A}}$ "Средний".

Если для любого кандидата ${ Displaystyle я neq c}$ , ${ Displaystyle альфа _ {я} < альфа _ {с}}$ , тогда ${ displaystyle c}$ получили более высокий средний рейтинг, чем все другие кандидаты, и ${ displaystyle c}$ выбирается независимо от того, какое правило наивысшей медианы было выбрано.

Когда разные кандидаты имеют одинаковый средний рейтинг, требуется правило разделения голосов. Это правило разрыва связей характеризует применяемое правило наивысшей медианы.

Правила разрешения споров часто используют две дополнительные статистические данные о кандидате. ${ displaystyle c}$ рейтинги:^[4]

В доля сторонников ${ displaystyle c}$ , отметил ${ displaystyle p_ {c}}$ , которая представляет собой долю избирателей, отнесенных к ${ displaystyle c}$ рейтинг выше среднего ${ displaystyle alpha _ {c}}$ . В приведенном выше примере три оценки "Хорошо" указаны выше. ${ displaystyle A}$ медиана "Среднее", поэтому ${ displaystyle p_ {A} = { frac {3} {10}}}$ .
В доля противников ${ displaystyle c}$ , отметил ${ displaystyle q_ {c}}$ , которая представляет собой долю избирателей, отнесенных к ${ displaystyle c}$ рейтинг ниже среднего ${ displaystyle alpha _ {c}}$ . В приведенном выше примере это соответствует оценке "Плохо", поэтому ${ displaystyle q_ {A} = { frac {1} {10}}}$ .

Примеры

Пример результата голосования, при котором каждый вариант (или кандидат) A, B, C или D побеждает в соответствии с одним из четырех изученных правил определения равенства: соответственно: типичное суждение (

{ displaystyle d}

), обычное суждение (

{ displaystyle s}

), центральное решение (

{ displaystyle n}

), и решение большинства (

{ displaystyle mj}

).^[4]

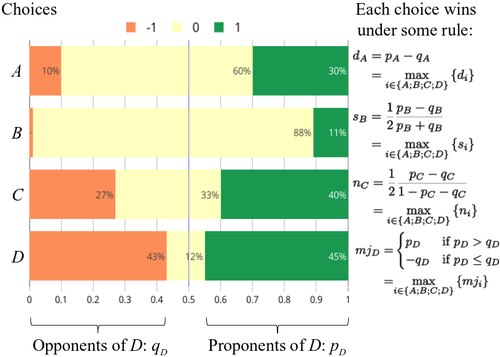
В типичное суждение упорядочивает кандидатов по наибольшей разнице между их долей сторонников и противников, т.е. по формуле:^[4] ${ Displaystyle д = альфа + р-д}$ (индексы ${ displaystyle c}$ опущены для простоты). В приведенном выше примере и определение "Средний" с оценкой ${ displaystyle 0}$ , у нас есть ${ displaystyle d_ {A} = 0 + 0,3-0,1 = + 0,2}$ .
В обычное суждение Говорят, что правило предлагает лучшие свойства,^[4] но он упорядочивает кандидатов по несколько более сложной формуле: ${ displaystyle n = alpha + { frac {1} {2}} { frac {p-q} {1-p-q}}}$ .
В центральное решение упорядочивает кандидатов в соответствии с наибольшим соотношением долей сторонников и противников, то есть по формуле: ${ displaystyle s = alpha + { frac {1} {2}} { frac {p-q} {p + q + epsilon}}}$ (куда ${ displaystyle epsilon}$ является сколь угодно малым числом, которое просто позволяет знаменателю оставаться положительным).
В решение большинства рассматривает кандидата, который ближе всего к рейтингу, отличному от его медианы, и прекращает равенство на основе этого рейтинга. Это эквивалентно упорядочиванию кандидатов по их баллам. ${ displaystyle mj}$ ,^[4] определяется следующей формулой (символ ${ displaystyle mathbf {1}}$ обозначает индикаторную функцию): ${ Displaystyle mj = альфа + mathbf {1} _ {p> q} p- mathbf {1} _ {p leq q} q}$ .
В Правила Баклина близки к правилам наивысшей медианы, но были разработаны для рейтинговые правила. Они заказывают кандидатов по формуле: ${ displaystyle b = alpha -q}$ . В ранжированном правиле это эквивалентно подсчету голосов первого выбора. Если один кандидат имеет большинство, он побеждает. В противном случае второй вариант добавляется к первому. Если найден кандидат с большинством голосов, победителем становится кандидат, набравший наибольшее количество голосов. При необходимости добавляются более низкие позиции.^[5]
Утверждающее голосование соответствует вырожденному случаю, когда есть только два возможных рейтинга: одобрение и неодобрение. В данном конкретном случае все правила разрешения ничьей эквивалентны, и Критерий Кондорсе доволен.^[6]