LC-цепь - LC circuit

Принципиальная схема LC

LC-цепь (оставили) состоящий из ферритовой катушки и конденсатора, используемых в качестве настраиваемой цепи в приемнике для радио часы

An LC-цепь, также называемый резонансный контур, резервуарный контур, или же настроенная схема, является электрическая цепь состоящий из индуктор, представленный буквой L, и конденсатор, представленные буквой C, соединены вместе. Схема может действовать как электрическая резонатор, электрический аналог камертон, накапливая энергию, колеблющуюся в цепи резонансная частота.

LC-схемы используются либо для генерации сигналов с определенной частотой, либо для выделения сигнала с определенной частотой из более сложного сигнала; эта функция называется полосовой фильтр. Они являются ключевыми компонентами многих электронных устройств, особенно радиооборудования, используемого в таких схемах, как генераторы, фильтры, тюнеры и частотные смесители.

LC-схема является идеальной моделью, поскольку предполагает, что нет рассеивания энергии из-за сопротивление. Любая практическая реализация LC-цепи всегда будет включать потери из-за небольшого, но ненулевого сопротивления компонентов и соединительных проводов. Целью LC-контура обычно является колебание с минимальным демпфирование, поэтому сопротивление должно быть минимальным. Хотя ни одна практическая схема не обходится без потерь, тем не менее поучительно изучить эту идеальную форму схемы, чтобы получить понимание и физическую интуицию. Для модели схемы, включающей сопротивление, см. Схема RLC.

Терминология

Описанная выше двухэлементная LC-схема представляет собой простейший тип индукторно-конденсаторная сеть (или же Сеть LC). Его также называют LC-цепь второго порядка чтобы отличить его от более сложных (более высокого порядка) LC-сетей с большим количеством индукторов и конденсаторов. Такие LC-сети с более чем двумя реактивными сопротивлениями могут иметь более одного резонансная частота.

Порядок сети - это порядок рациональная функция описывая сеть в комплексная частота Переменная $s$ . Как правило, порядок равен количеству элементов L и C в схеме и в любом случае не может превышать это количество.

Операция

Анимированная диаграмма, показывающая работу настроенная схема (LC-контур). Конденсатор C накапливает энергию в своем электрическое поле

E

а индуктор L накапливает энергию в своем магнитное поле

B

(зеленый). Анимация показывает схему в прогрессивных точках колебания. Колебания замедляются; в реальной настроенной цепи заряд может колебаться от тысячи до миллиардов раз в секунду.

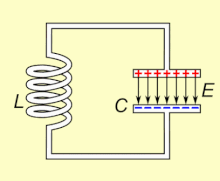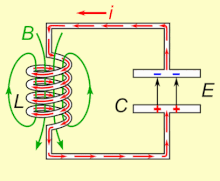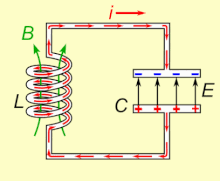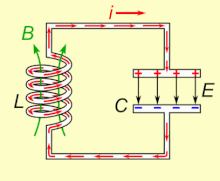
LC-контур, колеблющийся в естественном резонансная частота, можно хранить электроэнергия. Смотрите анимацию. Конденсатор накапливает энергию в электрическое поле ( $E$ ) между пластинами, в зависимости от Напряжение поперек него, а индуктор накапливает энергию в своем магнитное поле ( $B$ ), в зависимости от Текущий через это.

Если катушка индуктивности подключена к заряженному конденсатору, напряжение на конденсаторе будет пропускать ток через катушку индуктивности, создавая вокруг нее магнитное поле. Напряжение на конденсаторе падает до нуля, поскольку заряд расходуется текущим током. В этот момент энергия, запасенная в магнитном поле катушки, индуцирует напряжение на катушке, потому что индукторы противодействуют изменениям тока. Это индуцированное напряжение заставляет ток начать перезаряжать конденсатор с напряжением, противоположным полярности его первоначального заряда. Из-за Закон Фарадея, то ЭДС который управляет током, вызвано уменьшением магнитного поля, таким образом, энергия, необходимая для зарядки конденсатора, извлекается из магнитного поля. Когда магнитное поле полностью рассеивается, ток прекращается, и заряд снова сохраняется в конденсаторе с противоположной полярностью, как и раньше. Затем цикл начнется снова, и ток будет течь в обратном направлении через индуктор.

Заряд течет вперед и назад между пластинами конденсатора через катушку индуктивности. Энергия колеблется между конденсатором и катушкой индуктивности до тех пор, пока (если она не пополняется из внешней цепи) внутренняя сопротивление заставляет колебания затухать. Действие настроенной схемы, математически известное как гармонический осциллятор, похож на маятник раскачивание взад и вперед или плеск воды в баке; по этой причине схему также называют резервуарный контур.^[1] В собственная частота (то есть частота, с которой он будет колебаться при изолировании от любой другой системы, как описано выше) определяется значениями емкости и индуктивности. В большинстве приложений настроенная схема является частью более крупной схемы, которая применяется переменный ток к нему, вызывая непрерывные колебания. Если частота приложенного тока является собственной резонансной частотой цепи (собственная частота ${ displaystyle f_ {0} ,}$ ниже ), резонанс возникнет, и небольшой управляющий ток может возбуждать колебательные напряжения и токи большой амплитуды. В типичных настроенных схемах электронного оборудования колебания происходят очень быстро, от тысяч до миллиардов раз в секунду.

Резонансный эффект

Резонанс возникает, когда LC-цепь приводится в действие от внешнего источника с угловой частотой $ω 0$ при котором индуктивная и емкостная реактивные сопротивления равны по величине. Частота, при которой это равенство выполняется для конкретного контура, называется резонансной частотой. В резонансная частота LC-цепи

{ displaystyle omega _ {0} = { frac {1} { sqrt {LC}}},}

куда $L$ это индуктивность в Генри, и $C$ это емкость в фарады. В угловая частота $ω 0$ имеет единицы радианы в секунду.

Эквивалентная частота в единицах герц является

{ displaystyle f_ {0} = { frac { omega _ {0}} {2 pi}} = { frac {1} {2 pi { sqrt {LC}}}}.}

Приложения

Резонансный эффект LC-контура имеет много важных применений в системах обработки сигналов и связи.

Наиболее частым применением контуров резервуаров является настройка радиопередатчики и приемники. Например, при настройке радио на определенную станцию LC-контуры устанавливаются в резонанс для этой конкретной станции. несущая частота.
Последовательный резонансный контур обеспечивает увеличение напряжения.
Параллельный резонансный контур обеспечивает текущее увеличение.
Параллельный резонансный контур может использоваться в качестве сопротивления нагрузки в выходных цепях ВЧ усилителей. Из-за высокого импеданса коэффициент усиления усилителя максимален на резонансной частоте.
Как параллельные, так и последовательные резонансные цепи используются в индукционный нагрев.

LC-схемы ведут себя как электронные резонаторы, которые являются ключевым компонентом многих приложений:

Решение во временной области

Законы Кирхгофа

К Закон напряжения Кирхгофа, напряжение $V C$ через конденсатор плюс напряжение $V L$ на индукторе должно равняться нулю:

{ displaystyle V_ {C} + V_ {L} = 0.}

Точно так же Действующий закон Кирхгофа, ток через конденсатор равен току через индуктор:

{ displaystyle I_ {C} = I_ {L}.}

Из определяющих соотношений для элементов схемы мы также знаем, что

{ displaystyle { begin {align} V_ {L} (t) & = L { frac { mathrm {d} I_ {L}} { mathrm {d} t}}, I_ {C} ( t) & = C { frac { mathrm {d} V_ {C}} { mathrm {d} t}}. end {выравнивается}}}

Дифференциальное уравнение

Перестановка и замена дает второй порядок дифференциальное уравнение

{ displaystyle { frac { mathrm {d} ^ {2}} { mathrm {d} t ^ {2}}} I (t) + { frac {1} {LC}} I (t) = 0.}

Параметр $ω 0$ резонансный угловая частота, определяется как

{ displaystyle omega _ {0} = { frac {1} { sqrt {LC}}}.}

Используя это, можно упростить дифференциальное уравнение:

{ displaystyle { frac { mathrm {d} ^ {2}} { mathrm {d} t ^ {2}}} I (t) + omega _ {0} ^ {2} I (t) = 0.}

Связанный Преобразование Лапласа является

{ displaystyle s ^ {2} + omega _ {0} ^ {2} = 0,}

таким образом

{ displaystyle s = pm j omega _ {0},}

куда $j$ это мнимая единица.

Решение

Таким образом, полное решение дифференциального уравнения есть

{ displaystyle I (t) = Ae ^ {+ j omega _ {0} t} + Be ^ {- j omega _ {0} t}}

и может быть решена для $А$ и $B$ учитывая начальные условия. Поскольку экспонента равна сложный, решение представляет собой синусоидальную переменный ток. Поскольку электрический ток $я$ физическая величина, она должна иметь реальную стоимость. В результате можно показать, что константы $А$ и $B$ должно быть комплексные конъюгаты:

{ displaystyle A = B ^ {*}.}

Теперь позвольте

{ displaystyle A = { frac {I_ {0}} {2}} e ^ {+ j phi}.}

Следовательно,

{ displaystyle B = { frac {I_ {0}} {2}} e ^ {- j phi}.}

Далее мы можем использовать Формула Эйлера получить настоящий синусоида с амплитуда $я 0$ , угловая частота $ω 0 = 1 / \sqrt LC$ , и угол фазы ${ displaystyle phi}$ .

Таким образом, полученное решение становится

{ displaystyle I (t) = I_ {0} cos left ( omega _ {0} t + phi right),}

{ displaystyle V (t) = L { frac { mathrm {d} I} { mathrm {d} t}} = - omega _ {0} LI_ {0} sin left ( omega _ { 0} t + phi right).}

Первоначальные условия

Начальные условия, которые удовлетворяют этому результату, следующие:

{ Displaystyle I (0) = I_ {0} cos phi,}

{ Displaystyle V (0) = L { frac { mathrm {d} I} { mathrm {d} t}} { Bigg |} _ {t = 0} = - omega _ {0} LI_ { 0} sin phi.}

Последовательная схема

Последовательная цепь LC

В последовательной конфигурации LC-цепи катушка индуктивности (L) и конденсатор (C) соединены последовательно, как показано здесь. Общее напряжение $V$ на открытых клеммах - это просто сумма напряжения на катушке индуктивности и напряжения на конденсаторе. Электрический ток $я$ в положительный вывод цепи равен току через конденсатор и индуктивность.

{ displaystyle { begin {align} V & = V_ {L} + V_ {C}, I & = I_ {L} = I_ {C}. end {align}}}

Резонанс

Индуктивное реактивное сопротивление величина $Икс L$ увеличивается с увеличением частоты, а емкостное сопротивление величина $Икс C$ уменьшается с увеличением частоты. На одной конкретной частоте эти два реактивных сопротивления равны по величине, но противоположны по знаку; эта частота называется резонансной частотой $ж 0$ для данной схемы.

Следовательно, при резонансе

{ displaystyle { begin {align} X_ {L} & = X_ {C}, omega L & = { frac {1} { omega C}}. end {выравнивается}}}

Решение для $ω$ , у нас есть

{ displaystyle omega = omega _ {0} = { frac {1} { sqrt {LC}}},}

которая определяется как резонансная угловая частота контура. Преобразуя угловую частоту (в радианах в секунду) в частоту (в герцах), мы получаем

{ displaystyle f_ {0} = { frac { omega _ {0}} {2 pi}} = { frac {1} {2 pi { sqrt {LC}}}}.}

В серийной конфигурации $Икс C$ и $Икс L$ компенсируют друг друга. В реальных, а не идеализированных компонентах току противодействует, в основном, сопротивление обмоток катушки. Таким образом, ток, подаваемый в последовательный резонансный контур, максимален при резонансе.

В пределе как $ж \to ж 0$ ток максимальный. Сопротивление цепи минимальное. В этом состоянии цепь называется приемная цепь^[2]
За $ж < ж 0$ , $Икс L ≪ - Икс C$ . Следовательно, схема емкостная.
За $ж > ж 0$ , $Икс L ≫ - Икс C$ . Следовательно, цепь индуктивна.

Импеданс

В последовательной конфигурации резонанс возникает, когда комплексный электрический импеданс цепи приближается к нулю.

Сначала рассмотрим сопротивление последовательного LC-контура. Полный импеданс определяется суммой индуктивного и емкостного сопротивлений:

{ displaystyle Z = Z_ {L} + Z_ {C}.}

Записывая индуктивный импеданс как $Z L = jωL$ и емкостное сопротивление как $Z C = 1 / jωC$ и замена дает

{ displaystyle Z ( omega) = j omega L + { frac {1} {j omega C}}.}

Запись этого выражения под общим знаменателем дает

{ displaystyle Z ( omega) = j left ({ frac { omega ^ {2} LC-1} { omega C}} right).}

Наконец, определяя собственную угловую частоту как

{ displaystyle omega _ {0} = { frac {1} { sqrt {LC}}},}

импеданс становится

{ displaystyle Z ( omega) = jL left ({ frac { omega ^ {2} - omega _ {0} ^ {2}} { omega}} right).}

Из числителя следует, что в пределе при $ω \to \pm ω 0$ , полное сопротивление $Z$ будет равным нулю, а в противном случае ненулевым. Следовательно, последовательная LC-цепь при последовательном подключении к нагрузке будет действовать как полосовой фильтр имеющий нулевой импеданс на резонансной частоте LC-контура.

Параллельная схема

Параллельная LC-цепь

Когда катушка индуктивности (L) и конденсатор (C) подключены параллельно, как показано здесь, напряжение $V$ на открытых клеммах равно как напряжению на катушке индуктивности, так и напряжению на конденсаторе. Общий ток $я$ втекающий в положительный вывод схемы равен сумме тока, протекающего через катушку индуктивности, и тока, протекающего через конденсатор:

{ displaystyle { begin {align} V & = V_ {L} = V_ {C}, I & = I_ {L} + I_ {C}. end {align}}}

Резонанс

Когда $Икс L$ равно $Икс C$ , два тока ответвления равны и противоположны. Они компенсируют друг друга, чтобы получить минимальный ток в основной линии (в принципе, нулевой ток). Однако между конденсатором и катушкой индуктивности циркулирует большой ток. В принципе, этот циркулирующий ток бесконечен, но на самом деле он ограничен сопротивлением в цепи, особенно сопротивлением в обмотках индуктора. Так как общий ток минимален, в этом состоянии полное сопротивление будет максимальным.

Резонансная частота определяется выражением

{ displaystyle f_ {0} = { frac { omega _ {0}} {2 pi}} = { frac {1} {2 pi { sqrt {LC}}}}.}

Обратите внимание, что любой ток ветви не является минимальным при резонансе, но каждый дается отдельно путем деления напряжения источника ( $V$ ) реактивным сопротивлением ( $Z$ ). Следовательно $я = V / Z$ , согласно Закон Ома.

В $ж 0$ , линейный ток минимален. Общий импеданс максимальный. В этом состоянии цепь называется схема отражателя.^[3]
Ниже $ж 0$ , схема индуктивная.
Над $ж 0$ , схема емкостная.

Импеданс

Такой же анализ можно применить к параллельной LC-цепи. Тогда полный импеданс определяется как

{ displaystyle Z = { frac {Z_ {L} Z_ {C}} {Z_ {L} + Z_ {C}}},}

и после замены $Z L = jωL$ и $Z C = 1 / jωC$ и упрощение, дает

{ displaystyle Z ( omega) = - j cdot { frac { omega L} { omega ^ {2} LC-1}}.}

С помощью

{ displaystyle omega _ {0} = { frac {1} { sqrt {LC}}},}

это еще больше упрощает

{ Displaystyle Z ( omega) = - J влево ({ гидроразрыва {1} {C}} right) left ({ frac { omega} { omega ^ {2} - omega _ {0 } ^ {2}}} right).}

Обратите внимание, что

{ displaystyle lim _ { omega to omega _ {0}} Z ( omega) = infty,}

но для всех остальных значений $ω$ импеданс конечен. Параллельная LC-цепь, включенная последовательно с нагрузкой, будет действовать как полосовой фильтр имеющий бесконечный импеданс на резонансной частоте LC-контура. Параллельная LC-цепь, подключенная параллельно нагрузке, будет действовать как полосовой фильтр.

Решение Лапласа

Цепь LC может быть решена с помощью Преобразование Лапласа.

Пусть общее уравнение будет:

{ Displaystyle v_ {C} (т) = v (т)}

{ Displaystyle я (т) = С { гидроразрыва { mathrm {d} v_ {C}} { mathrm {d} t}}}

{ displaystyle v_ {L} (t) = L { frac { mathrm {d} i} { mathrm {d} t}}}

Пусть дифференциальное уравнение серии LC имеет вид:

{ displaystyle v_ {in} (t) = v_ {L} (t) + v_ {C} (t) = L { frac { mathrm {d} i} { mathrm {d} t}} + v = LC { frac { mathrm {d} ^ {2} v} { mathrm {d} t ^ {2}}} + v}

С начальным состоянием:

{ Displaystyle { begin {case} v (0) = v_ {0} i (0) = i_ {0} = C cdot v '(0) = C cdot v' _ {0} end {случаи}}}

Определим:

{ displaystyle omega _ {0} = { frac {1} { sqrt {LC}}}}

{ displaystyle f (t) = omega _ {0} ^ {2} v_ {in} (t)}

Дает:

{ displaystyle f (t) = { frac { mathrm {d} ^ {2} v} { mathrm {d} t ^ {2}}} + omega _ {0} ^ {2} v}

Преобразование с помощью Лапласа:

{ displaystyle { mathcal {L}} left [f (t) right] = { mathcal {L}} left [{ frac { mathrm {d} ^ {2} v} { mathrm { d} t ^ {2}}} + omega _ {0} ^ {2} v right]}

{ Displaystyle F (s) = s ^ {2} V (s) -sv_ {0} -v '_ {0} + omega _ {0} ^ {2} V (s)}

{ displaystyle V (s) = { frac {sv_ {0} + v '_ {0} + F (s)} {s ^ {2} + omega _ {0} ^ {2}}}}

Тогда антитрансформация:

{ displaystyle v (t) = v_ {0} cos ( omega _ {0} t) + { frac {v '_ {0}} { omega _ {0}}} sin ( omega _ {0} t) + { mathcal {L}} ^ {- 1} left [{ frac {F (s)} {s ^ {2} + omega _ {0} ^ {2}}} верно]}

Если входное напряжение Ступенчатая функция Хевисайда:

{ displaystyle v_ {in} (t) = Mu (t)}

{ displaystyle { mathcal {L}} ^ {- 1} left [ omega _ {0} ^ {2} { frac {V_ {in} (s)} {s ^ {2} + omega _ {0} ^ {2}}} right] = { mathcal {L}} ^ {- 1} left [ omega _ {0} ^ {2} M { frac {1} {s (s ^ {2} + omega _ {0} ^ {2})}} right] = M (1- cos ( omega _ {0} t))}

{ displaystyle v (t) = v_ {0} cos ( omega _ {0} t) + { frac {v '_ {0}} { omega _ {0}}} sin ( omega _ {0} t) + M (1- cos ( omega _ {0} t))}

Если входное напряжение является синусоидальной функцией:

{ displaystyle v_ {in} (t) = U sin ( omega _ {f} t) Rightarrow V_ {in} (s) = { frac {U omega _ {f}} {s ^ {2 } + omega _ {f} ^ {2}}}}

{ displaystyle { mathcal {L}} ^ {- 1} left [ omega _ {0} ^ {2} { frac {1} {s ^ {2} + omega _ {0} ^ {2 }}} { frac {U omega _ {f}} {s ^ {2} + omega _ {f} ^ {2}}} right] = { mathcal {L}} ^ {- 1} left [{ frac { omega _ {0} ^ {2} U omega _ {f}} { omega _ {f} ^ {2} - omega _ {0} ^ {2}}} слева ({ frac {1} {s ^ {2} + omega _ {0} ^ {2}}} - { frac {1} {s ^ {2} + omega _ {f} ^ {2 }}} right) right] = { frac { omega _ {0} ^ {2} U omega _ {f}} { omega _ {f} ^ {2} - omega _ {0} ^ {2}}} left ({ frac {1} { omega _ {0}}} sin ( omega _ {0} t) - { frac {1} { omega _ {f}} } sin ( omega _ {f} t) right)}

{ displaystyle v (t) = v_ {0} cos ( omega _ {0} t) + { frac {v '_ {0}} { omega _ {0}}} sin ( omega _ {0} t) + { frac { omega _ {0} ^ {2} U omega _ {f}} { omega _ {f} ^ {2} - omega _ {0} ^ {2} }} left ({ frac {1} { omega _ {0}}} sin ( omega _ {0} t) - { frac {1} { omega _ {f}}} sin ( omega _ {f} t) right)}

История

Первое свидетельство того, что конденсатор и индуктор могут вызывать электрические колебания, было обнаружено в 1826 году французским ученым. Феликс Савари.^[4]^[5] Он обнаружил, что когда лейденская банка разряжался через проволоку, намотанную на железную иглу, иногда иглу оставляли намагниченной в одном направлении, а иногда в противоположном. Он правильно пришел к выводу, что это было вызвано затухающим колеблющимся током разряда в проводе, который менял намагниченность иглы назад и вперед до тех пор, пока она не становилась слишком маленькой, чтобы оказывать влияние, оставляя иглу намагниченной в случайном направлении. Американский физик Джозеф Генри повторил эксперимент Савари в 1842 году и пришел к тому же выводу, по-видимому, независимо.^[6]^[7] Ирландский ученый Уильям Томсон (Лорд Кельвин) в 1853 году математически показал, что разряд лейденской банки через индуктивность должен быть колебательным, и определил его резонансную частоту.^[4]^[6]^[7] Британский радиоисследователь Оливер Лодж, разряжая большую батарею лейденских банок через длинный провод, создавал настроенный контур с его резонансной частотой в звуковом диапазоне, который производил музыкальный тон из искры, когда она разряжалась.^[6] В 1857 году немецкий физик Беренд Вильгельм Феддерсен сфотографировал искру, создаваемую резонансным контуром лейденской банки во вращающемся зеркале, обеспечивая видимые свидетельства колебаний.^[4]^[6]^[7] В 1868 году шотландский физик Джеймс Клерк Максвелл рассчитал эффект от приложения переменного тока к цепи с индуктивностью и емкостью, показав, что отклик максимален на резонансной частоте.^[4] Первый пример электрического резонанс Кривая была опубликована в 1887 г. немецким физиком Генрих Герц в своей новаторской статье об открытии радиоволн, показывающей длину искры, получаемой от его детекторов LC-резонатора с искровым разрядником, как функцию частоты.^[4]

Одна из первых демонстраций резонанс Между настроенными схемами был эксперимент Лоджа с «синтонными сосудами» около 1889 года.^[4]^[6] Он разместил рядом друг с другом две резонансные цепи, каждая из которых состояла из лейденской банки, соединенной с регулируемой одновитковой катушкой с искровым разрядником. Когда высокое напряжение от индукционной катушки прикладывалось к одному настроенному контуру, создавая искры и, следовательно, колеблющиеся токи, искры возбуждались в другом настроенном контуре только тогда, когда контуры были настроены на резонанс. Лодж и некоторые английские ученые предпочли термин "синтония"для этого эффекта, но срок"резонанс"в конце концов застрял.^[4] Первое практическое использование LC-цепей было в 1890-х годах в искровые радиопередатчики для настройки приемника и передатчика на одну и ту же частоту. Первый патент на радиосистему, которая позволяла настройку, был подан Лоджем в 1897 году, хотя первые практические системы были изобретены в 1900 году итальянским пионером в области радиосвязи. Гульельмо Маркони.^[4]

Смотрите также

внешняя ссылка

Электрический маятник Тони Купальдт - классический рассказ о работе танка LC
Как схема с параллельным LC хранит энергию - еще один отличный ресурс LC.

[Rao-1] Рао, Б. Вишвешвара; и другие. (2012). Анализ электронных схем. Индия: Pearson Education India. п. 13.6. ISBN 978-9332511743.

[2] Что такое цепь приемника.

[3] "режекторный контур". Оксфордские словари. английский. Получено 2018-09-20.

[Blanchard-4] а ^б ^c ^d ^е ^ж ^грамм ^час Бланшар, Джулиан (октябрь 1941 г.). «История электрического резонанса». Технический журнал Bell System. США: American Telephone & Telegraph Co. 20 (4): 415–433. Дои:10.1002 / j.1538-7305.1941.tb03608.x. S2CID 51669988. Получено 2011-03-29.

[5] Савари, Феликс (1827). «Воспоминания о еде». Annales de Chimie et de Physique. Париж: Массон. 34: 5–37.

[Kimball-6] а ^б ^c ^d ^е Кимбалл, Артур Лаланн (1917). Учебник физики для колледжа (2-е изд.). Нью-Йорк: Генри Холд. стр.516 –517.

[Huurdeman-7] а ^б ^c Huurdeman, Антон А. (2003). Всемирная история телекоммуникаций. США: Wiley-IEEE. С. 199–200. ISBN 0-471-20505-2.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

LC-цепь - LC circuit

Содержание

Терминология

Операция

Резонансный эффект

Приложения

Решение во временной области

Законы Кирхгофа

Дифференциальное уравнение

Решение

Первоначальные условия

Последовательная схема

Резонанс

Импеданс

Параллельная схема

Резонанс

Импеданс

Решение Лапласа

История

Смотрите также

Рекомендации

внешняя ссылка