Линейная сейсмическая инверсия - Википедия - Linear seismic inversion
Обратное моделирование представляет собой математический метод, цель которого состоит в том, чтобы определить физические свойства подповерхностного слоя земного региона, который произвел данный сейсмограмма. Кук и Шнайдер (1983)[1] определил это как расчет структуры Земли и физических параметры из некоторого набора наблюдаемых сейсмический данные. Основное предположение в этом методе состоит в том, что собранные сейсмические данные относятся к земной структуре, которая соответствует поперечному сечению, вычисленному по инверсии алгоритм.[2] Некоторые общие свойства земли, которые инвертируются, включают скорость звука, формирование и жидкость плотности, акустический импеданс, Коэффициент Пуассона, сжимаемость пласта, жесткость на сдвиг, пористость, и флюидонасыщенность.
Этот метод давно используется геофизиками и может быть разделен на два основных типа:[3] Детерминированный и стохастический инверсия. Методы детерминированной инверсии основаны на сравнении выходных данных модели недр с данными наблюдаемых полей и постоянном обновлении параметров модели недр для минимизации функции, которая обычно представляет собой некоторую форму разницы между выходными данными модели и полевыми наблюдениями. Таким образом, этот метод инверсии, к которому подпадает линейная инверсия, ставится как проблема минимизации, а принятая модель земли - это набор параметров модели, который минимизирует целевая функция в создании числовой сейсмограммы, которая лучше всего сравнивается с собранными полевыми сейсмическими данными.
С другой стороны, методы стохастической инверсии используются для создания моделей с ограничениями, которые используются в резервуар моделирование потока с использованием геостатистических инструментов, таких как кригинг. В отличие от методов детерминированной инверсии, которые производят единый набор параметров модели, стохастические методы генерируют набор альтернативных параметров модели недр, которые все подчиняются ограничениям модели. Однако эти два метода связаны, поскольку результаты детерминированных моделей представляют собой среднее значение всех возможных неуникальных решений стохастических методов.[3] Поскольку сейсмическая линейная инверсия является детерминированным методом инверсии, стохастический метод не будет обсуждаться дальше этого пункта.
Линейная инверсия
В детерминированный природа линейная инверсия требует функциональный отношения, моделирующие в терминах модели земли параметры - инвертируемая сейсмическая переменная. Эта функциональная связь представляет собой некую математическую модель, основанную на фундаментальных законах физики, и ее чаще называют прямой моделью. Цель метода - минимизировать функцию, которая зависит от разницы между сверткой прямой модели с источником. вейвлет и поле собрано сейсмическая трасса. Как и в области оптимизации, эта функция, которую необходимо минимизировать, называется целевая функция а в конвекционном инверсном моделировании - это просто разница между свернутой прямой моделью и сейсмической трассой. Как упоминалось ранее, различные типы переменных могут быть инвертированы, но для ясности эти переменные будут называться сопротивление серия модели земли. В следующих подразделах мы более подробно опишем в контексте линейной инверсии как задачи минимизации различные компоненты, которые необходимы для инверсии сейсмических данных.
Форвардная модель
Центральным элементом сейсмической линейной инверсии является прямая модель, которая моделирует создание собранных экспериментальных данных.[1] Согласно Виггинсу (1972),[4] он обеспечивает функциональную (вычислительную) связь между параметрами модели и расчетными значениями наблюдаемых трасс. В зависимости от собранных сейсмических данных эта модель может отличаться от классической. волновые уравнения для предсказания смещение частиц или давление жидкости для распространения звуковой волны через горную породу или флюиды, к некоторым вариантам этих классических уравнений. Например, форвардная модель в Тарантоле (1984)[5] является волновым уравнением для изменения давления в жидкой среде во время распространения сейсмических волн, в то время как в предположении слоев с постоянной скоростью и плоскими границами раздела, Канасевич и Чиу (1985)[6] использовал модель брахистотрона Джона Бернулли для времени путешествия луч по тропинке. В Cooke and Schneider (1983),[1] модель представляет собой синтетический алгоритм генерации трассировки, выраженный как в уравнении. 3, где R (t) генерируется в Z-области по рекурсивной формуле. В какой бы форме ни появилась прямая модель, важно, чтобы она не только предсказывала собранные полевые данные, но и моделировала их генерацию. Таким образом, передовая модель Кука и Шнайдера (1983)[1] может использоваться только для инвертирования данных CMP, поскольку модель неизменно предполагает отсутствие потерь за счет имитации реакции бокового однородный Земля к источнику плоских волн
- где t - время прохождения луча, x, y, z - координаты глубины, а vi - постоянная скорость между интерфейсами i - 1 и i.
- куда представляют собой объемный модуль, плотность, источник акустических волн, и изменение давления.
куда s(т) = синтетический след, ш(т) = исходный вейвлет, и р(т) = функция отражательной способности.
Целевая функция
Важным численным процессом в обратном моделировании является минимизация целевой функции, которая является функцией, определяемой в терминах разницы между собранными полевыми сейсмическими данными и численно вычисленными сейсмическими данными. Классические целевые функции включают сумму квадратов отклонений между экспериментальными и численными данными, как в наименьших квадратов методы, сумма величина различия между полевыми и числовыми данными или какой-либо вариант этих определений. Независимо от используемого определения численное решение обратной задачи получается как модель земли, минимизирующая целевую функцию.
Помимо целевой функции, в процедуру обратного моделирования также включаются другие ограничения, такие как известные параметры модели и известные границы раздела слоев в некоторых регионах Земли. Эти ограничения, согласно Фрэнсису 2006 г.,[3] помогают уменьшить неединственность решения инверсии, предоставляя априорную информацию, которая не содержится в инвертированных данных, в то время как Cooke и Schneider (1983)[1] сообщает об их полезности при контроле шума и при работе в хорошо известной геофизической зоне.
Математический анализ процедуры обобщенного линейного обращения
Целью математического анализа обратного моделирования является преобразование обобщенной линейной обратной задачи в простую форму. матрица алгебры, учитывая все компоненты, описанные в предыдущих разделах. а именно; прямая модель, целевая функция и т. д. Как правило, полученные численно сейсмические данные являются нелинейными функциями параметров модели недр. Чтобы убрать нелинейность и создать платформу для применения линейная алгебра концепции, передовая модель линеаризованный путем расширения с использованием Серия Тейлор как показано ниже. Подробнее см. Wiggins (1972),[4] Кук и Шнайдер (1983).[1]
Рассмотрим набор полевые сейсмические наблюдения , за и набор параметры модели земли быть инвертированным для, для . Полевые наблюдения могут быть представлены в виде или же , куда и являются векторными представлениями параметров модели и полевых наблюдений как функции параметров земли. Аналогично для представление предположений о параметрах модели, - вектор численно вычисленных сейсмических данных с использованием прямой модели из разд. 1.3. Расширение серии Тейлора о приведен ниже.
- При линеаризации путем отбрасывания нелинейных членов (членов с (p⃗ - ⃗q) порядка 2 и выше) уравнение становится
- Учитывая, что имеет компоненты и и имеют компоненты, дискретная форма уравнения. 5 результатов в системе линейные уравнения в переменные, матричная форма которых показана ниже.
называется разница вектор в Cooke and Schneider (1983).[1] Он имеет размер а его компоненты - это разница между наблюдаемой трассой и численно рассчитанными сейсмическими данными. - вектор корректора размера , пока называется матрицей чувствительности. Он имеет размер и его комментарии таковы, что каждый столбец является частная производная компонента прямой функции относительно одного из неизвестных параметров модели земли. Аналогичным образом, каждая строка является частной производной компонента численно вычисленной сейсмической трассы по всем неизвестным параметрам модели.
Алгоритм решения
вычисляется из прямой модели, а - экспериментальные данные. Таким образом, это известное качество. С другой стороны, неизвестна и получается путем решения уравнения. 10. Это уравнение теоретически разрешимо только при обратима, то есть если это квадратная матрица, так что количество наблюдений равно числу неизвестных параметров земли. Если это так, неизвестный вектор корректора , решается для, как показано ниже, с использованием любого из классических прямых или итерационных решателей для решения набора линейных уравнений.
В большинстве сейсмическая инверсия приложений, существует больше наблюдений, чем количество параметров земли, которые нужно инвертировать, т. е. , что приводит к математически переопределенной системе уравнений. В результате уравнение. 10 теоретически не разрешима, и точное решение невозможно.[6] Оценка вектора корректора получается с использованием процедуры наименьших квадратов для нахождения вектора корректора что сводит к минимуму , который представляет собой сумму квадратов ошибки, .[6]
Ошибка дан кем-то
В методе наименьших квадратов вектор корректора, который минимизирует получается, как показано ниже.
Таким образом,
Из приведенных выше обсуждений целевая функция определяется как или же норма данный или же или из данный или же .
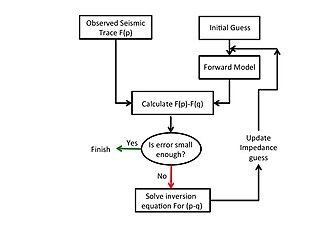
Обобщенная процедура инвертирования любых экспериментальных сейсмических данных для или же , использующий математическую теорию для обратного моделирования, как описано выше, показан на рис. 1 и описывается следующим образом.
Первоначальное предположение об импедансе модели предоставляется для запуска процесса инверсии. Прямая модель использует это начальное предположение для вычисления синтетических сейсмических данных, которые вычитаются из наблюдаемых сейсмических данных для вычисления вектора разности.
- Первоначальное предположение об импедансе модели предоставляется для запуска процесса инверсии.
- Синтетические сейсмические данные вычисляется прямой моделью с использованием импеданса модели выше.
- Вектор разности вычисляется как разница между экспериментальными и синтетическими сейсмическими данными.
- Матрица чувствительности вычисляется при этом значении профиля импеданса.
- С помощью и вектор разности из 3 выше, вектор корректора рассчитывается. Новый профиль импеданса получается как
- В или же Норма вычисленного вектора корректора сравнивается с заданным значением допуска. Если вычисленная норма меньше допустимого отклонения, численная процедура завершается и обратный профиль импеданса для земной области определяется как из уравнения. 14. С другой стороны, если норма больше, чем допуск, итерации через шаги 2-6 повторяются, но с обновленным профилем импеданса, вычисленным по формуле. 14. Рис. 2[7] показывает типичный пример обновления профиля импеданса во время последовательной итерации. По словам Кука и Шнайдера (1983),[1] использование исправленного предположения из уравнения. 14, поскольку новое начальное предположение во время итерации уменьшает ошибку.
Параметризация пространства модели Земли
Независимо от переменной, которая должна быть инвертирована, импеданс земли является непрерывной функцией глубины (или времени в сейсмических данных), и для того, чтобы метод численной линейной инверсии был применим для этой непрерывной физической модели, непрерывные свойства должны быть дискретизированы и / или с дискретными интервалами по глубине модели земли. Таким образом, общая глубина, на которой должны определяться свойства модели, является необходимой отправной точкой для дискретизации. Обычно, как показано на рис. 3, эти свойства отбираются через близкие дискретные интервалы на этой глубине, чтобы гарантировать высокое разрешение изменения импеданса по глубине земли. Значения импеданса, инвертированные относительно алгоритм представляет собой среднее значение в дискретном интервале.
Учитывая, что обратная задача моделирования может быть решена только теоретически, когда количество дискретных интервалов для выборки свойств равно количеству наблюдений в трассе, которую нужно инвертировать, выборка с высоким разрешением приведет к большой матрице, что будет очень дорого. инвертировать. Кроме того, матрица может быть сингулярной для зависимых уравнений, инверсия может быть нестабильной в присутствии шума, и система может быть недостаточно ограниченной, если желательны параметры, отличные от первичных переменных, для которых инвертированы. Что касается желаемых параметров, кроме импеданса, Cooke and Schneider (1983)[1] дает им включить исходный вейвлет и масштабный коэффициент.
Наконец, рассматривая ограничения как известные значения импеданса в некоторых слоях или дискретных интервалах, количество решаемых неизвестных значений импеданса уменьшается, что приводит к большей точности результатов алгоритма инверсии.



Примеры инверсии
Температурная инверсия от Marescot (2010)[8]
Мы начнем с примера, чтобы инвертировать значения параметров земли из распределения температуры по глубине в данном регионе земли. Хотя этот пример не имеет прямого отношения к сейсмическая инверсия поскольку не используются бегущие акустические волны, он тем не менее вводит практическое применение техники инверсии в простой для понимания манере, прежде чем перейти к сейсмическим приложениям. В этом примере температура земли измеряется в отдельных точках ствола скважины путем размещения датчиков температуры на заданных глубинах. Принимая прямую модель линейного распределения температуры по глубине, два параметра инвертируются на основе измерений температуры на глубине.
Форвардная модель представлена
куда . Таким образом, размерность равно 2, т.е. число инвертированных параметров равно 2.
Цель этого алгоритма инверсии - найти , что является значением что сводит к минимуму разницу между наблюдаемым распределением температуры и полученными с использованием прямой модели уравнения. 15. Рассмотрение размеров прямой модели или количества температурных наблюдений, которые необходимо провести. , компоненты форвардной модели записываются как
- так что
Мы представляем результаты Marescot (2010)[8] для случая для которых наблюдаемые значения температуры на глубине были в и в . Эти экспериментальные данные были инвертированы для получения значений параметров земли и . Для более общего случая с большим количеством наблюдений температуры на рис.4 показана окончательная линейная прямая модель, полученная с использованием инвертированных значений и . На рисунке показано хорошее совпадение экспериментальных и численных данных.
Инверсия времени распространения волны от Marescot (2010)[8]
Этот пример инвертирует для слоя земли скорость по зарегистрированным временам пробега сейсмических волн. На рис. 5 показаны предположения о начальной скорости и время пробега, записанные с поля, а на рис. 6а показаны обратные неоднородный скоростная модель, которая является решением алгоритма обращения, полученным после 30 итерации. Как видно на рис. 6b, есть хорошее сравнение между окончательными временами пробега, полученными из прямой модели с использованием инвертированной скорости, и временами пробега полевого рекорда. Используя эти решения, была восстановлена траектория луча, которая, как показано на рис.7, является очень извилистой в модели земли.
Инверсия сейсмических трасс от Кука и Шнайдера (1983)
Этот пример взят из Cooke and Schneider (1983),[1] показывает инверсию сейсмической трассы ОГТ для профиля импеданса модели земли (произведение плотности и скорости). Инвертированная сейсмическая трасса показана на рис. 8, а на рис. 9а показан перевернутый профиль импеданса с входным начальным импедансом, используемым для алгоритма инверсии. Кроме того, рядом с сейсмической трассой записывается каротаж импеданса земной области, как показано на рис. 9b. Рисунки показывают хорошее сравнение между записанным каротажем импеданса и численным инвертированным импедансом из сейсмической трассы.
Рекомендации
- ^ а б c d е ж грамм час я j Кук, Д. А .; Шнайдер В. А. (июнь 1983 г.). «Обобщенная линейная инверсия отраженных сейсмических данных». Геофизика. 48 (6): 665–676. Дои:10.1190/1.1441497.
- ^ Pica, A .; Diet J. P .; Тарантола А. (март 1990 г.). «Нелинейная инверсия данных сейсмических отражений в латерально инвариантной среде». Геофизика. 55 (3): 284–292. Дои:10.1190/1.1442836.
- ^ а б c Фрэнсис, А. (Ноябрь 2006 г.). «Понимание стохастической и сейсмической инверсии». Первый перерыв. 24 (11). Дои:10.3997/1365-2397.2006026.
- ^ а б Виггинс, Ральф (февраль 1972 г.). «Общая линейная обратная задача: влияние поверхностных волн и свободных колебаний на структуру Земли». Обзоры геофизики. 10 (1): 251–285. Дои:10.1029 / RG010i001p00251.
- ^ Тарантола, А. (1984). "Линеаризация и инверсия сейсмических данных отражения". Геофизическая разведка. 32 (6): 908–1015. Дои:10.1111 / j.1365-2478.1984.tb00751.x.
- ^ а б c Kanasewich, E. R .; Чиу С. К. Л. (июнь 1985 г.). "Инверсия методом наименьших квадратов пространственных данных сейсмической рефракции". Бюллетень сейсмологического общества Америки. 75 (3): 865–880.
- ^ Кук, Д. Кант Дж. (Апрель 2010 г.). «Модельная сейсмическая инверсия: сравнение детерминированного и вероятностного подходов». Регистратор CSEG.
- ^ а б c Мареско, Лоран. «Введение в инверсию в геофизике». Получено 3 мая 2013.
дальнейшее чтение
- Бэкус, Г. 1970. «Вывод из неадекватных и неточных данных». Proceedings of the National Academy of Sciences of the United States of America 65, no. 1.
- Бэкус, Г., и Ф. Гилберт. 1968. «Разрешающая способность совокупных данных о Земле». Геофизический журнал Королевского астрономического общества 16 (2): 169–205.
- Бэкус Г. Э. и Дж. Ф. Гилберт. 1967. «Численные приложения формализма для обратных геофизических задач». Геофизический журнал Королевского астрономического общества. 13 (1-3): 247.
- Бамбергер А., Дж. Чавент, К. Хемон и П. Лайи. 1982. «Инверсия сейсомограмм нормальной заболеваемости». Геофизика 47 (5): 757–770.
- Clayton, R. W. и R. H. Stolt. 1981. «Метод инверсии Born-WKBJ для данных акустического отражения». Геофизика 46 (11): 1559–1567.
- Франклин, Дж. Н. 1970. «Корректные стохастические расширения некорректных линейных задач». Журнал математического анализа и приложений 31 (3): 682.
- Паркер, Р. Л. 1977. «Понимание обратной теории». Ежегодный обзор наук о Земле и планетах 5: 35–64.
- Роулинсон, Н. 2000. «Инверсия сейсмических данных для слоистой структуры земной коры». Кандидат наук. дисс., Университет Монаш.
- Ван Б. и Л. В. Брейл. 1996. «Одновременная инверсия сейсмических данных по отражениям и преломлениям и их применение к полевым данным северного рифта Рио-Гранде». Международный геофизический журнал 125 (2): 443–458.
- Weglein, A. B., H. Y. Zhang, A. C. Ramirez, F. Liu, J. E. M. Lira. 2009. «Уточнение основного и фундаментального смысла приблизительной линейной инверсии сейсмических данных». Геофизика 74 (6): 6WCD1 – WCD13.

![{ displaystyle t = sum _ {i = 1} ^ {n} { frac {{ big [} (x_ {i} -x_ {i-1}) ^ {2} + (y_ {i} - y_ {i-1}) ^ {2} + (z_ {i} -z_ {i-1}) ^ {2} { big]} ^ { frac {1} {2}}} {v_ {i }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f527eee1cff061b7fcccc13cf601afce95425f45)
![{ displaystyle left [{ frac {1} {K ({ vec {r}})}} { frac { partial ^ {2}} { partial t ^ {2}}} - nabla cdot { big (} { frac {1} { rho ({ vec {r}} { big)}}} nabla) right] U ({ vec {r}}, t) = s ({ vec {r}}, t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18ef1cf0e83874d9c657988e24e9c527d8e837ef)
















































![{ Displaystyle { vec {q}} = [а, б]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e439f51761b9272857b0e16ccad659d3cddf8f2)
![[а, б]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)











