Уравнения движения поршня - Piston motion equations

Эта статья не цитировать любой источники. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удаленный. Найдите источники: «Уравнения движения поршня»  – Новости  · газеты  · книги  · ученый  · JSTOR (Декабрь 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Движение без смещения поршень подключен к заводить через шатун (как можно найти в двигатель внутреннего сгорания ), можно выразить через несколько математические уравнения. В этой статье показано, как выводятся эти уравнения движения, и показан пример графика.

Геометрия коленчатого вала

Схема, показывающая геометрическое расположение поршневого пальца, кривошипного пальца и центра кривошипа

Определения

${displaystyle l}$ стержень длина (расстояние между поршневой палец и шатун )

${displaystyle r}$ заводить радиус (дистанция между шатун и центр кривошипа, т.е. половина Инсульт )

${displaystyle A}$ угол поворота коленчатого вала (от цилиндр сверлить осевая линия на ВМТ )

${displaystyle x}$ положение поршневого пальца (вверх от центра кривошипа по средней линии отверстия цилиндра)

${displaystyle v}$ скорость поршневого пальца (вверх от центра кривошипа по средней линии отверстия цилиндра)

${displaystyle a}$ ускорение поршневого пальца (вверх от центра кривошипа по средней линии отверстия цилиндра)

${displaystyle omega}$ заводить угловая скорость

Угловая скорость

В коленчатый вал угловая скорость связано с двигателем число оборотов в минуту (Об / мин):

${displaystyle omega = {frac {2pi cdot mathrm {RPM}} {60}}}$

Отношение треугольника

Как показано на схеме, шатун, центр кривошипа и поршневой палец образуют треугольник NOP.
Посредством закон косинуса видно, что:

${displaystyle l ^ {2} = r ^ {2} + x ^ {2} -2cdot rcdot xcdot cos A}$

Уравнения относительно углового положения (угловая область)

Следующие уравнения описывают возвратно-поступательное движение поршня относительно угла поворота коленчатого вала. Примеры графиков этих уравнений показаны ниже.

Позиция

Положение относительно угла поворота коленчатого вала (из соотношения треугольника, завершение квадрата, используя Пифагорейская идентичность, и переставляя):

${displaystyle {egin {array} {lcl} l ^ {2} = r ^ {2} + x ^ {2} -2cdot rcdot xcdot cos A l ^ {2} -r ^ {2} = (x-rcdot cos A) ^ {2} -r ^ {2} cdot cos ^ {2} A l ^ {2} -r ^ {2} + r ^ {2} cdot cos ^ {2} A = (x-rcdot cos A) ^ {2} l ^ {2} -r ^ {2} cdot (1-cos ^ {2} A) = (x-rcdot cos A) ^ {2} l ^ {2} -r ^ {2} cdot sin ^ {2} A = (x-rcdot cos A) ^ {2} x = rcdot cos A + {sqrt {l ^ {2} -r ^ {2} cdot sin ^ {2} A }} end {массив}}}$

Скорость

Скорость относительно угла поворота коленчатого вала (сначала возьмите производная, с использованием Правило цепи ):

${displaystyle {egin {array} {lcl} x '& = & {frac {dx} {dA}} & = & - rcdot sin A + {frac {({frac {1} {2}}) cdot (-2 ) cdot r ^ {2} cdot sin Acdot cos A} {sqrt {l ^ {2} -r ^ {2} cdot sin ^ {2} A}}} & = & - rcdot sin A- {frac {r ^ {2} cdot sin Acdot cos A} {sqrt {l ^ {2} -r ^ {2} cdot sin ^ {2} A}}} end {array}}}$

Ускорение

Ускорение относительно угла поворота коленчатого вала (второй производная, с использованием Правило цепи и правило частного ):

${displaystyle {egin {array} {lcl} x '' & = & {frac {d ^ {2} x} {dA ^ {2}}} & = & - rcdot cos A- {frac {r ^ {2 } cdot cos ^ {2} A} {sqrt {l ^ {2} -r ^ {2} cdot sin ^ {2} A}}} - {frac {-r ^ {2} cdot sin ^ {2} A } {sqrt {l ^ {2} -r ^ {2} cdot sin ^ {2} A}}} - {frac {r ^ {2} cdot sin Acdot cos Acdot left (- {frac {1} {2} } ight) cdot (-2) cdot r ^ {2} cdot sin Acdot cos A} {left ({sqrt {l ^ {2} -r ^ {2} cdot sin ^ {2} A}} ight) ^ { 3}}} & = & - rcdot cos A- {frac {r ^ {2} cdot left (cos ^ {2} A-sin ^ {2} Aight)} {sqrt {l ^ {2} -r ^ {2} cdot sin ^ {2} A}}} - {frac {r ^ {4} cdot sin ^ {2} Acdot cos ^ {2} A} {left ({sqrt {l ^ {2} -r ^ {2} cdot sin ^ {2} A}} ight) ^ {3}}} end {array}}}$

Уравнения относительно времени (временная область)

Производные угловой скорости

Если угловая скорость постоянна, то

${displaystyle A = omega t,}$

и применяются следующие отношения:

${displaystyle {frac {dA} {dt}} = omega}$

${displaystyle {frac {d ^ {2} A} {dt ^ {2}}} = 0}$

Преобразование из угловой области во временную

Следующие уравнения описывают возвратно-поступательное движение поршня по времени. Если область времени требуется вместо углового домена, сначала замените A на ωt в уравнениях, а затем шкала для угловой скорости следующим образом:

Позиция

Положение относительно времени просто:

${displaystyle x,}$

Скорость

Скорость по времени (используя Правило цепи ):

${displaystyle {egin {array} {lcl} v & = & {frac {dx} {dt}} & = & {frac {dx} {dA}} cdot {frac {dA} {dt}} & = & { frac {dx} {dA}} cdot omega & = & x'cdot omega end {array}}}$

Ускорение

Ускорение по времени (используя Правило цепи и правило продукта, а угловая скорость производные ):

${displaystyle {egin {array} {lcl} a & = & {frac {d ^ {2} x} {dt ^ {2}}} & = & {frac {d} {dt}} {frac {dx} { dt}} & = & {frac {d} {dt}} ({frac {dx} {dA}} cdot {frac {dA} {dt}}) & = & {frac {d} {dt}} ({frac {dx} {dA}}) cdot {frac {dA} {dt}} + {frac {dx} {dA}} cdot {frac {d} {dt}} ({frac {dA} {dt} }) & = & {frac {d} {dA}} ({frac {dx} {dA}}) cdot ({frac {dA} {dt}}) ^ {2} + {frac {dx} {dA }} cdot {frac {d ^ {2} A} {dt ^ {2}}} & = & {frac {d ^ {2} x} {dA ^ {2}}} cdot ({frac {dA} {dt}}) ^ {2} + {frac {dx} {dA}} cdot {frac {d ^ {2} A} {dt ^ {2}}} & = & {frac {d ^ {2} x} {dA ^ {2}}} cdot omega ^ {2} + {frac {dx} {dA}} cdot 0 & = & x''cdot omega ^ {2} end {array}}}$

Масштабирование угловой скорости

Вы можете видеть, что x не масштабируется, x масштабируется на ω, а x "масштабируется на ω². Чтобы преобразовать x 'из скорости в зависимости от угла [дюйм / рад] в скорость в зависимости от времени [дюйм / с], умножьте x' на ω [рад / с]. Чтобы преобразовать x "из ускорения в зависимости от угла [дюйм / рад²] в ускорение в зависимости от времени [дюйм / с²], умножьте x» на ω² [рад² / с²]. Обратите внимание, что размерный анализ показывает, что единицы согласуются.

Максимумы / минимумы скорости

Переход через ноль ускорения

Скорость максимумы и минимумы возникают при углах поворота коленвала, где ускорение равно нулю (пересечение горизонтальной оси). Максимумы и минимумы скорости зависят от длины стержня. (l) и половина хода (р), и делать нет возникают при углах поворота коленвала (А) ± 90 °.

Угол шатуна не прямой

Максимумы и минимумы скорости не обязательно происходить когда кривошип находится под прямым углом к ​​штоку. Существуют контрпримеры, чтобы опровергнуть идея эти максимумы и минимумы скорости возникают только тогда, когда угол поворота коленчатого вала является прямым.

Пример

Для длины штанги 6 дюймов и радиуса кривошипа 2 (как показано на приведенном ниже примере графика) численное решение пересечений нуля ускорения обнаруживает, что максимумы / минимумы скорости находятся при углах поворота кривошипа ± 73,17615 °. Затем, используя треугольник закон синуса, обнаружено, что угол между штоком и вертикалью составляет 18,60647 °, а угол поворота коленчатого вала - 88,21738 °. Очевидно, что в этом примере угол между кривошипом и стержнем не является прямым. Суммируя углы треугольника 88,21738 ° + 18,60647 ° + 73,17615 °, получаем 180,00000 °. Единственного контрпримера достаточно, чтобы опровергнуть заявление «максимумы / минимумы скорости возникают, когда кривошип находится под прямым углом к ​​штоку».

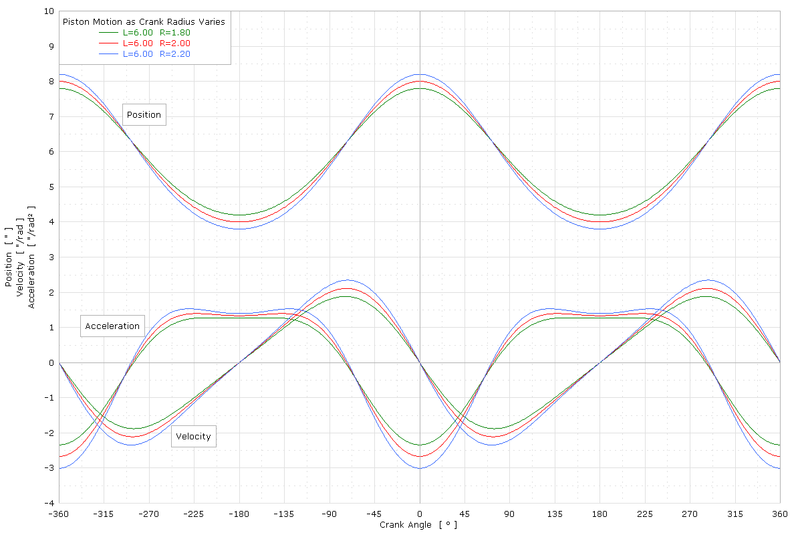
Пример графика движения поршня

На графике показаны x, x ', x "относительно угла поворота коленчатого вала для различных половин хода, где L = длина штока. (l) и R = половина хода (р):

Единицы вертикальной оси: дюймы для положения, [дюймы / рад] для скорости, [дюймы / рад²] для ускорения.
Блоки горизонтальной оси - угол поворота коленчатого вала градусы.

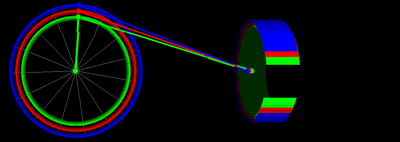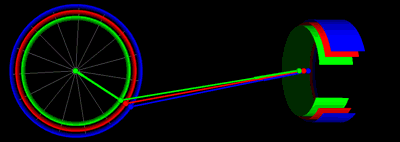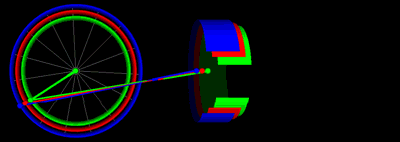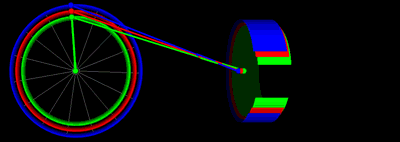
Анимация движения поршня при одинаковых значениях длины штока и радиуса кривошипа на графике выше:

Анимация движения поршней с различными половинными ходами

Смотрите также

• Двигатель внутреннего сгорания
• Поршневой двигатель
• Ползунковый рычажный механизм
• Скотч-кокетка

Рекомендации

1. http://www.epi-eng.com/piston_engine_technology/piston_motion_basics.htm

дальнейшее чтение

• Джон Бенджамин Хейвуд, Основы двигателя внутреннего сгорания, Макгроу Хилл, 1989.
• Чарльз Файетт Тейлор, Двигатель внутреннего сгорания в теории и практике. 1 и 2, 2-е издание, MIT Press 1985.

внешняя ссылка

• epi-eng Поршневое движение
• кодекоги Скорость и ускорение поршня
• анимированные двигатели Четырехтактный двигатель
• Desmos интерактивная анимация кривошипа
• сети Механизмы D&T - Интерактивные инструменты для учителей
• Mecamedia анимация движения поршня

• YouTube Вращающийся шеви 350 короткий блок.
• YouTube 3D-анимация ДВИГАТЕЛЯ V8
• YouTube Внутри двигателя V8 на холостом ходу
• Desmos интерактивный ход по отношению к соотношению штока, положение поршня и производные