Расположение точки - Point location
Эта статья включает Список ссылок, связанное чтение или внешняя ссылка, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. (июнь 2013) (Узнайте, как и когда удалить этот шаблон сообщения) |
В точка расположения проблема является фундаментальной темой вычислительная геометрия. Он находит применения в областях, связанных с обработкой геометрических данных: компьютерная графика, географические информационные системы (ГИС), планирование движения, и системы автоматизированного проектирования (CAD).
В самом общем виде задача состоит в том, чтобы, учитывая разделение пространства на непересекающиеся области, определить область, в которой находится точка запроса. В качестве примера приложения каждый раз, когда вы щелкаете мышью, чтобы перейти по ссылке в веб-браузер, эту проблему необходимо решить, чтобы определить, какая область экрана компьютера находится под указателем мыши. Простой частный случай - это точка в многоугольнике проблема. В этом случае нам нужно определить, находится ли точка внутри, снаружи или на границе одного многоугольника.
Во многих приложениях нам необходимо определить расположение нескольких разных точек по отношению к одному и тому же разделу пространства. Для эффективного решения этой проблемы полезно построить структура данных который, учитывая точку запроса, быстро определяет, какой регион содержит точку запроса (например, Диаграмма Вороного ).
Планарный корпус

В плоском случае мы получаем планарное подразделение S, образованный множеством полигоны называемые лица, и необходимо определить, какое лицо содержит точку запроса. А поиск грубой силы каждого лица с помощью точка в многоугольнике алгоритм возможен, но обычно не реализуем для подразделений высокой сложности. Несколько различных подходов приводят к оптимальным структурам данных, с О (п) место для хранения и O (журнал п) время запроса, где п это общее количество вершин в S. Для простоты мы предполагаем, что планарное подразделение содержится внутри квадратной ограничительной рамки.
Разложение плиты

Самая простая и самая ранняя структура данных для достижения O (log п) время было открыто Добкин и Lipton в 1976 году. Он основан на разделении S используя вертикальные линии, проходящие через каждую вершину в S. Область между двумя последовательными вертикальными линиями называется плитой. Обратите внимание, что каждая плита разделена непересекающимися линейными сегментами, которые полностью пересекают плиту слева направо. Область между двумя последовательными сегментами внутри плиты соответствует уникальной грани S. Поэтому мы сводим нашу задачу определения местоположения к двум более простым задачам:
- Учитывая разделение плоскости на вертикальные плиты, определите, какая плита содержит данную точку.
- Учитывая, что плита разделена на области непересекающимися сегментами, которые полностью пересекают плиту слева направо, определите, какая область содержит данную точку.
Первую проблему можно решить с помощью бинарный поиск на Икс координата вертикальных линий в O (log п) время. Вторую проблему тоже можно решить за O (log п) время двоичным поиском. Чтобы понять, как это сделать, обратите внимание на то, что, поскольку сегменты не пересекаются и полностью пересекают перекрытие, сегменты можно сортировать по вертикали внутри каждого перекрытия.
Хотя этот алгоритм позволяет определять местоположение точки в логарифмическом времени и его легко реализовать, пространство, необходимое для построения плит и областей, содержащихся внутри плит, может достигать O (п²), поскольку каждая плита может пересекать значительную часть сегментов.
Несколько авторов заметили, что сегменты, пересекающие две соседние плиты, в основном одинаковы. Следовательно, размер структуры данных можно значительно уменьшить. В частности, Сарнак и Тарджан проводят вертикальную линию. л слева направо по плоскости, сохраняя пересекающиеся сегменты л в Настойчивый красно-черное дерево. Это позволяет им уменьшить объем памяти до O (п), сохраняя O (log п) время запроса.
Монотонные подразделения

(Вертикальная) монотонная цепочка - это дорожка так что у-координата никогда не увеличивается по пути. А простой многоугольник является (вертикальным) монотонным, если он образован двумя монотонными цепями с общими первой и последней вершинами. Можно добавить несколько ребер к плоскому подразделению, чтобы сделать все грани монотонными, получив так называемое монотонное подразделение. Этот процесс не добавляет вершин к подразделению (следовательно, размер остается O (п)) и может выполняться за O (п бревно п) время по развертка (это также можно выполнить за линейное время, используя триангуляция многоугольника ). Следовательно, не будет потери общности, если мы ограничим нашу структуру данных случаем монотонных подразделений, как мы это делаем в этом разделе.
Слабым местом декомпозиции плиты является то, что вертикальные линии создают дополнительные сегменты при декомпозиции, что затрудняет достижение O (п) пространство для хранения. Эдельсбруннер, Гибас, и Stolfi обнаружил оптимальную структуру данных, которая использует только ребра в монотонном подразделении. Идея состоит в том, чтобы использовать вертикальные монотонные цепочки вместо использования вертикальных линий для разделения подразделения.
Преобразование этой общей идеи в реальную эффективную структуру данных - непростая задача. Во-первых, нам нужно иметь возможность вычислить монотонную цепочку, которая делит подразделение на две половины одинакового размера. Во-вторых, поскольку некоторые ребра могут содержаться в нескольких монотонных цепочках, мы должны быть осторожны, чтобы гарантировать, что объем памяти равен O (n). В-третьих, проверка того, находится ли точка слева или справа от монотонного подразделения, занимает O (п) время, если выполнено наивно.
Подробная информация о том, как решить первые две проблемы, выходит за рамки этой статьи. Кратко упомянем, как решить третью проблему. Используя двоичный поиск, мы можем проверить, находится ли точка слева или справа от монотонной цепочки в O (log п) время. Поскольку нам нужно выполнить еще один вложенный двоичный поиск через O (log п) цепочки для фактического определения местоположения точки, время запроса составляет O (log² n). Для достижения O (log п) время запроса, нам нужно использовать дробное каскадирование, сохраняя указатели между краями разных монотонных цепочек.
Уточнение триангуляции
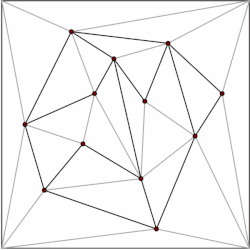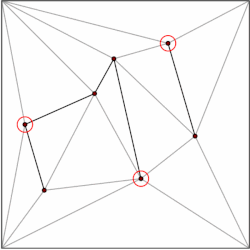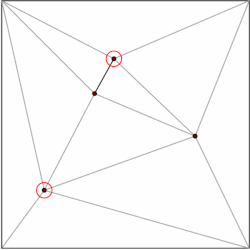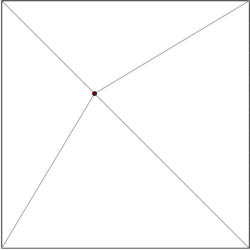
Многоугольник с м вершины можно разбить на м–2 треугольника. Что может быть показано индукция начиная с треугольника. Есть множество алгоритмов для триангулировать многоугольник эффективно, самый быстрый имея O (п) худшее время. Следовательно, мы можем разложить каждый многоугольник нашего подразделения на треугольники и ограничить нашу структуру данных случаем подразделений, образованных исключительно треугольниками. Киркпатрик дает структуру данных для местоположения точки в триангулированных подразделениях с O (п) место для хранения и O (журнал п) время запроса.
Общая идея состоит в том, чтобы построить иерархию треугольников. Чтобы выполнить запрос, мы начинаем с поиска треугольника верхнего уровня, который содержит точку запроса. Поскольку количество треугольников верхнего уровня ограничено константой, эту операцию можно выполнить за время O (1). Каждый треугольник имеет указатели на треугольники, которые он пересекает на следующем уровне иерархии, и количество указателей также ограничено константой. Мы продолжаем запрос, выясняя, какой треугольник содержит точку запроса, уровень за уровнем.
Структура данных строится в обратном порядке, то есть снизу вверх. Мы начинаем с триангулированного подразделения и выбираем независимый набор удаляемых вершин. После удаления вершин мы ретриангулируем подразделение. Поскольку подразделение состоит из треугольников, жадный алгоритм может найти независимый набор, содержащий постоянную долю вершин. Следовательно, количество шагов удаления равно O (log п).
Трапециевидное разложение

А рандомизированный подход к этой проблеме, и, наверное, самый практичный, основан на трапециевидное разложение, или карту трапеции. Трапецеидальное разложение получается путем стрельбы вертикальными пулями, идущими вверх и вниз из каждой вершины в исходном подразделении. Пули останавливаются, когда попадают в край, и образуют новый край в подразделении. Таким образом, мы получаем подмножество разложения плиты только с O (п) ребер и вершин, поскольку для каждой вершины в исходном подразделении мы добавляем только две новые вершины и увеличиваем количество ребер на четыре.
Непросто понять, как использовать трапециевидное разложение для определения местоположения точки, поскольку двоичный поиск, аналогичный тому, который используется в разложении плиты, больше не может выполняться. Вместо этого нам нужно ответить на запрос так же, как при подходе к уточнению триангуляции, но структура данных строится сверху вниз. Первоначально мы строим трапециевидную декомпозицию, содержащую только ограничивающую рамку, но не внутреннюю вершину. Затем мы добавляем сегменты из подразделения, один за другим, в случайном порядке, уточняя трапециевидное разложение. С помощью обратный анализ, мы можем показать, что ожидаемое количество трапеций, создаваемых для каждой вставки, ограничено константой.
Мы строим ориентированный ациклический граф, где вершины - это трапеции, существовавшие в какой-то момент уточнения, а направленные ребра соединяют трапеции, полученные с помощью подразделения. Ожидаемая глубина поиска в этом орграфе, начиная с вершины, соответствующей ограничивающему прямоугольнику, равна O (log п)[требуется разъяснение ].
Высшие измерения
Нет известных общих структур данных местоположения точек с линейным пространством и логарифмическим временем запроса для измерений больше 2.[нужна цитата ]. Следовательно, нам нужно пожертвовать либо временем запроса, либо пространством для хранения, либо ограничиться каким-либо менее общим типом подразделения.
В трехмерном пространстве можно ответить на запросы о местоположении точки за O (log² п) используя O (п бревно п) Космос. Общая идея состоит в том, чтобы поддерживать несколько плоских структур данных местоположения точек, соответствующих пересечению подразделения с п параллельные плоскости, содержащие каждую вершину подразделения. Наивное использование этой идеи увеличило бы объем памяти до O (п²). Таким же образом, как и при декомпозиции slab, сходство между последовательными структурами данных может быть использовано для уменьшения пространства хранения до O (п бревно п), но время запроса увеличивается до O (log² п).[нужна цитата ]
В d-мерное пространство, местоположение точки может быть решено путем рекурсивного проецирования граней в (d-1) -мерное пространство. Пока время запроса O (журнал п), объем памяти может достигать . Высокая сложность d-мерные структуры данных привели к изучению особых типов подразделения.
Одним из важных примеров является случай расположение гиперплоскостей. Расположение п гиперплоскости определяет O (пd) ячеек, но определение местоположения точки может быть выполнено за O (журнал п) время с O (пd) пространство с помощью Chazelle иерархическая черенки.
Другой особый тип деления называется прямолинейным (или ортогональным) делением. При прямолинейном делении все ребра параллельны одному из d ортогональная ось. В этом случае на местоположение точки можно ответить за O (журналd-1 п) время с O (п) Космос.
Рекомендации
- де Берг, Марк; ван Кревельд, Марк; Овермарс, Марк; Шварцкопф, Отфрид (2000). «Глава 6: Местоположение точки». Вычислительная геометрия (2-е изд. Перераб.). Springer-Verlag. стр.121–146. ISBN 3-540-65620-0.
- Добкин, Давид; Липтон, Ричард Дж. (1976). «Проблемы многомерного поиска». SIAM Журнал по вычислениям. 5 (2): 181–186. Дои:10.1137/0205015.
- Snoeyink, Джек (2004). "Глава 34:" Местоположение точки ". Гудман, Джейкоб Э.; О'Рурк, Джозеф (ред.). Справочник по дискретной и вычислительной геометрии (2-е изд.). Чепмен и Холл / CRC. ISBN 1-58488-301-4.
- Сарнак, Нил; Тарджан, Роберт Э. (1986). «Расположение точек на плоскости с использованием постоянных деревьев поиска». Коммуникации ACM. 29 (7): 669–679. Дои:10.1145/6138.6151.
- Эдельсбруннер, Герберт; Гибас, Леонидас Дж.; Столфи, Хорхе (1986). «Оптимальное расположение точки на монотонном участке». SIAM Журнал по вычислениям. 15 (2): 317–340. Дои:10.1137/0215023.
- Киркпатрик, Дэвид Г. (1983). «Оптимальный поиск в плоских сечениях». SIAM Журнал по вычислениям. 12 (1): 28–35. CiteSeerX 10.1.1.461.1866. Дои:10.1137/0212002.
внешняя ссылка
- Репозиторий источников местоположения точек в Университете Стоуни Брук
- Запросы о местоположении точки в CGAL, Библиотека алгоритмов вычислительной геометрии

