Студентизированное распределение диапазона - Studentized range distribution

Студентизированное распределение диапазона

Функция плотности вероятности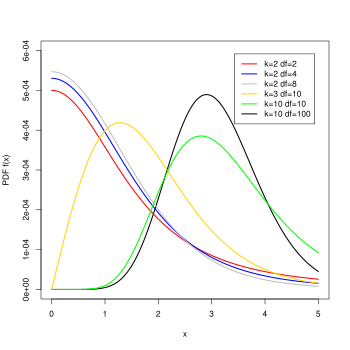
Кумулятивная функция распределения
Параметры	k > 1, количество групп ${ displaystyle nu}$ > 0, то степени свободы
Поддерживать	${ Displaystyle д в (0, + infty)}$
PDF	${ displaystyle { begin {matrix} f _ { text {R}} (q; k, nu) = { frac {, { sqrt {2 pi ,}} , k , (k -1) , nu ^ { nu / 2} ,} { Gamma ( nu / 2) , 2 ^ { left ( nu / 2-1 right)}}} int _ { 0} ^ { infty} s ^ { nu} , varphi ({ sqrt { nu ,}} , s) , times [0.5em] left [ int _ {- infty} ^ { infty} varphi (z + q , s) , varphi (z) , left [ Phi (z + q , s) - Phi (z) right] ^ {k-2} , mathrm {d} z right] , mathrm {d} s end {matrix}}}$
CDF	${ displaystyle { begin {matrix} F _ { text {R}} (q; k, nu) = { frac {, { sqrt {2 pi ,}} , k , nu ^ { nu / 2} ,} {, Gamma ( nu / 2) , 2 ^ { left ( nu / 2-1 right)}}} int _ {0} ^ { infty} s ^ { nu -1} , varphi ({ sqrt { nu ,}} , s) , times [0.5em] qquad left [ int _ {- infty} ^ { infty} varphi (z) , left [ Phi (z + q , s) - Phi (z) right] ^ {k-1} , mathrm {d} z right] , mathrm {d} s end {matrix}}}$

В вероятность и статистика, студентизированное распределение диапазона является непрерывным распределение вероятностей из стьюдентизированный диапазон из i.i.d. образец из нормально распределенный численность населения.

Предположим, что мы берем образец размером п от каждого из k населения с одинаковыми нормальное распределение N(μ, σ²) и предположим, что ${ displaystyle { bar {y}} _ { min}}$ - наименьшее из этих выборочных средних и ${ displaystyle { bar {y}} _ { max}}$ является наибольшим из этих выборочных средних, и предположим, что s² - это совокупное отклонение выборки от этих выборок. Тогда следующая случайная величина имеет распределение по стьюдентизированному диапазону.

${ displaystyle q = { frac {{ overline {y}} _ { max} - { overline {y}} _ { min}} {s / { sqrt {n ,}}}}}$

Определение

Функция плотности вероятности

Дифференцируя кумулятивную функцию распределения по q дает функция плотности вероятности.

${ displaystyle f _ { text {R}} (q; k, nu) = { frac {{ sqrt {2 pi ,}} , k , (k-1) , nu ^ { nu / 2}} { Gamma ( nu / 2) , 2 ^ { left ( nu / 2-1 right)}}} int _ {0} ^ { infty} s ^ { nu} , varphi ({ sqrt { nu ,}} , s) , left [ int _ {- infty} ^ { infty} varphi (z + q , s) , varphi (z) , left [ Phi (z + q , s) - Phi (z) right] ^ {k-2} , mathrm {d} z right] , mathrm {d} s}$

Отметим, что во внешней части интеграла уравнение

${ displaystyle varphi ({ sqrt { nu ,}} , s) , { sqrt {2 pi ,}} = e ^ {- left ( nu , s ^ ​​{2} / 2 right)}}$

был использован для замены экспоненциального множителя.

Кумулятивная функция распределения

Кумулятивная функция распределения определяется выражением ^[1]

${ displaystyle F _ { text {R}} (q; k, nu) = { frac {{ sqrt {2 pi ,}} , k , nu ^ { nu / 2}} {, ​​ Gamma ( nu / 2) , 2 ^ {( nu / 2-1)} ,}} int _ {0} ^ { infty} s ^ { nu -1} varphi ({ sqrt { nu ,}} , s) left [ int _ {- infty} ^ { infty} varphi (z) left [ Phi (z + q , s) - Phi (z) right] ^ {k-1} , mathrm {d} z right] , mathrm {d} s}$

Особые случаи

Если k 2 или 3,^[2] стьюдентизированная функция распределения вероятностей диапазона может быть непосредственно оценена, где ${ Displaystyle varphi (г)}$ - стандартная нормальная функция плотности вероятности и ${ displaystyle Phi (z)}$ - стандартная нормальная кумулятивная функция распределения.

${ displaystyle f_ {R} (q; k = 2) = { sqrt {2 ,}} , varphi left (, q / { sqrt {2 ,}} right)}$

${ displaystyle f_ {R} (q; k = 3) = 6 { sqrt {2 ,}} , varphi left (, q / { sqrt {2 ,}} right) left [ Phi left (q / { sqrt {6 ,}} right) - { tfrac {1} {2}} right]}$

Когда степени свободы приближаются к бесконечности, кумулятивное распределение стьюдентизированного диапазона может быть вычислено для любого k с использованием стандартного нормального распределения.

${ Displaystyle F_ {R} (д; к) = к , int _ {- infty} ^ { infty} varphi (z) , { Bigl [} Phi (z + q) - Phi (z) { Bigr]} ^ {k-1} , mathrm {d} z = k , int _ {- infty} ^ { infty} , { Bigl [} Phi ( z + q) - Phi (z) { Bigr]} ^ {k-1} , mathrm {d} Phi (z)}$

Приложения

Критические значения стьюдентизированного распределения диапазонов используются в Тест дальности Тьюки.

Студентизированный диапазон используется для расчета уровней значимости результатов, полученных сбор данных, где выборочно ищут крайние различия в данных выборки, а не только случайную выборку.

Распределение диапазонов Studentized имеет приложения для проверка гипотезы и множественные сравнения процедуры. Например, Тест дальности Тьюки и Новый многодиапазонный тест Дункана (MRT), в котором образец Икс₁, ..., Икс_п это образец средства и q - основная статистика теста, может использоваться как апостериорный анализ чтобы проверить, между какими двумя группами имеется значительная разница (попарные сравнения) после отклонения нулевая гипотеза что все группы принадлежат к одной и той же популяции (т.е. все средства равны) по стандарту дисперсионный анализ.^[3]

Связанные дистрибутивы

Когда ставится под сомнение только равенство двух групп средств (т.е. μ₁ = μ₂), стьюдентизированное распределение диапазона похоже на Распределение Стьюдента, отличаясь только тем, что первое учитывает количество рассматриваемых средств, а критическое значение корректируется соответствующим образом. Чем больше рассматриваемых средств, тем больше критическое значение. Это имеет смысл, поскольку чем больше имеется средств, тем больше вероятность того, что хотя бы некоторые различия между парами средних будут значительны только благодаря случайности.

Вывод

Стьюдентизированная функция распределения диапазона возникает в результате повторного масштабирования диапазона выборки. р посредством стандартное отклонение выборки s, поскольку стьюдентизированный диапазон обычно табулируется в единицах стандартных отклонений, с переменной q = ​^р⁄_s. Вывод начинается с совершенно общей формы функции распределения диапазона выборки, которая применяется к любому распределению выборочных данных.

Для получения распределения по «студентизированному» диапазону q, мы заменим переменную с р к s и q. Предполагая, что данные образца нормально распределенный, то стандартное отклонение s будет χ распределен. Путем дальнейшей интеграции по s мы можем удалить s в качестве параметра и получить масштабированное распределение в терминах q один.

Общая форма

Для любой функции плотности вероятности ж_Икс, дальность плотности вероятности ж_р является:^[2]

${ displaystyle f_ {R} (r; k) = k , (k-1) int _ {- infty} ^ { infty} f_ {X} left (t + { tfrac {1} {2) }} r right) f_ {X} left (t - { tfrac {1} {2}} r right) left [ int _ {t - { tfrac {1} {2}} r} ^ {t + { tfrac {1} {2}} r} f_ {X} (x) , mathrm {d} x right] ^ {k-2} , mathrm {d} , t}$

Это означает, что мы складываем вероятности, которые, учитывая k взяты из раздачи, два из них отличаются р, а остальные k - 2 рисунка попадают между двумя крайними значениями. Если мы заменим переменные на ты куда ${ Displaystyle и = т - { tfrac {1} {2}} г}$ это нижний предел диапазона, и определите F_Икс как кумулятивная функция распределения ж_Икс, то уравнение можно упростить:

${ displaystyle f_ {R} (r; k) = k , (k-1) int _ {- infty} ^ { infty} f_ {X} (u + r) , f_ {X} ( u) , left [, F_ {X} (u + r) -F_ {X} (u) , right] ^ {k-2} , mathrm {d} , u}$

Введем аналогичный интеграл и заметим, что дифференцирование под знаком интеграла дает

${ displaystyle { begin {align} { frac { partial} { partial r}} & left [k , int _ {- infty} ^ { infty} f_ {X} (u) , { Bigl [} , F_ {X} (u + r) -F_ {X} (u) , { Bigr]} ^ {k-1} , mathrm {d} , u right ] [5pt] = {} & k , (k-1) int _ {- infty} ^ { infty} f_ {X} (u + r) , f_ {X} (u) , { Bigl [} , F_ {X} (u + r) -F_ {X} (u) , { Bigr]} ^ {k-2} , mathrm {d} , u end { выровнено}}}$

который восстанавливает интеграл выше,^[а] так что последнее соотношение подтверждает

${ Displaystyle { begin {align} F_ {R} (r; k) & = k int _ {- infty} ^ { infty} f_ {X} (u) { Bigl [} , F_ { X} (u + r) -F_ {X} (u) , { Bigr]} ^ {k-1} , mathrm {d} , u & = k int _ {- infty } ^ { infty} { Bigl [} , F_ {X} (u + r) -F_ {X} (u) , { Bigr]} ^ {k-1} , mathrm {d} , F_ {X} (и) конец {выровнено}}}$

потому что для любого непрерывного cdf

${ displaystyle { frac { partial F_ {R} (r; k)} { partial r}} = f_ {R} (r; k)}$

Специальная форма для обычных данных

Распределение диапазона чаще всего используется для доверительных интервалов вокруг выборочных средних, которые асимптотически нормально распределенный посредством Центральная предельная теорема.

Чтобы создать стьюдентизированное распределение диапазонов для нормальных данных, мы сначала переключаемся с общего ж_Икс и F_Икс к функциям распределения φ и Φ для стандартное нормальное распределение, и изменим переменную р к s · q, куда q фиксированный коэффициент, который изменяет масштаб р по коэффициенту масштабирования s:

${ displaystyle f_ {R} (q; k) = s , k , (k-1) int _ {- infty} ^ { infty} varphi (u + sq) varphi (u) , left [, Phi (u + sq) - Phi (u) right] ^ {k-2} , mathrm {d} u}$

Выберите коэффициент масштабирования s быть стандартным отклонением выборки, так что q становится числом стандартных отклонений в пределах диапазона. Для нормальных данных s является чи распределяется^[b] и функция распределения ж_S распределения ци дан кем-то:

${ displaystyle f_ {S} (s; nu) , mathrm {d} s = { begin {case} { dfrac { nu ^ { nu / 2} , s ^ ​​{ nu -1 } e ^ {- nu , s ^ ​​{2} / 2} ,} {2 ^ { left ( nu / 2-1 right)} Gamma ( nu / 2)}} , mathrm {d} s & { text {for}} , 0$

Умножение распределений ж_р и ж_S и интегрирование, чтобы удалить зависимость от стандартного отклонения s дает стьюдентифицированную функцию распределения диапазонов для нормальных данных:

${ displaystyle f_ {R} (q; k, nu) = { frac { nu ^ { nu / 2} , k , (k-1)} {2 ^ { left ( nu / 2-1 right)} Gamma ( nu / 2)}} int _ {0} ^ { infty} s ^ { nu} e ^ {- nu s ^ {2} / 2} int _ {- infty} ^ { infty} varphi (u + sq) , varphi (u) , left [, Phi (u + sq) - Phi (u) right] ^ { к-2} , mathrm {d} и , mathrm {d} s}$

куда

q - ширина диапазона данных, измеренная в стандартных отклонениях,

ν - количество степеней свободы для определения стандартного отклонения выборки,^[c] и

k - количество отдельных средних значений, образующих точки в пределах диапазона.

Уравнение для pdf показанное в разделах выше, происходит от использования

${ Displaystyle е ^ {- nu , s ^ ​​{2} / 2} = { sqrt {2 pi ,}} , varphi ({ sqrt { nu ,}} , s) }$

для замены экспоненциального выражения во внешнем интеграле.

Примечания