Распределение Ци - Chi distribution

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален Найдите источники: «Распределение Чи»  – Новости  · газеты  · книги  · ученый  · JSTOR (Октябрь 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

чи

Функция плотности вероятности
Кумулятивная функция распределения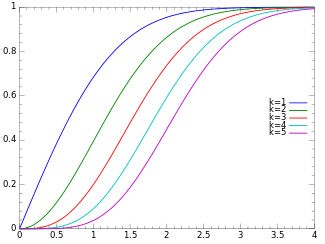
Параметры	${ displaystyle k> 0 ,}$ (степени свободы)
Поддерживать	${ Displaystyle х в [0, infty)}$
PDF	${ Displaystyle { frac {1} {2 ^ {(k / 2) -1} Gamma (k / 2)}} ; x ^ {k-1} e ^ {- x ^ {2} / 2 }}$
CDF	${ Displaystyle P (к / 2, х ^ {2} / 2) ,}$
Иметь в виду	${ displaystyle mu = { sqrt {2}} , { frac { Gamma ((k + 1) / 2)} { Gamma (k / 2)}}}$
Медиана	${ displaystyle приблизительно { sqrt {к { bigg (} 1 - { frac {2} {9k}} { bigg)} ^ {3}}}}$
Режим	${ displaystyle { sqrt {k-1}} ,}$ за ${ Displaystyle к geq 1}$
Дисперсия	${ Displaystyle sigma ^ {2} = к- му ^ {2} ,}$
Асимметрия	${ displaystyle gamma _ {1} = { frac { mu} { sigma ^ {3}}} , (1-2 sigma ^ {2})}$
Бывший. эксцесс	${ displaystyle { frac {2} { sigma ^ {2}}} (1- mu sigma gamma _ {1} - sigma ^ {2})}$
Энтропия	${ Displaystyle пер ( гамма (к / 2)) + ,}$ ${ Displaystyle { гидроразрыва {1} {2}} (к ! - ! ln (2) ! - ! (k ! - ! 1) psi _ {0} (k / 2) )}$
MGF	Сложный (см. Текст)
CF	Сложный (см. Текст)

В теория вероятности и статистика, то распределение ци является непрерывным распределение вероятностей. Это распределение положительного квадратного корня из суммы квадратов набора независимых случайных величин, каждая из которых соответствует стандартной нормальное распределение, или, что то же самое, распределение Евклидово расстояние случайных величин из начала координат. Таким образом, это связано с распределение хи-квадрат путем описания распределения положительных квадратных корней переменной, подчиняющейся распределению хи-квадрат.

Если ${ Displaystyle Z_ {1}, ldots, Z_ {k}}$ находятся ${ displaystyle k}$ независимый, нормально распределенный случайные величины со средним 0 и стандартное отклонение 1, то статистика

${ displaystyle Y = { sqrt { sum _ {i = 1} ^ {k} Z_ {i} ^ {2}}}}$

распределяется согласно распределению ци. Распределение хи имеет один параметр, ${ displaystyle k}$, который определяет количество степени свободы (т.е. количество ${ displaystyle Z_ {i}}$).

Наиболее известные примеры: Распределение Рэлея (распределение ци с двумя степени свободы ) и Распределение Максвелла – Больцмана молекулярных скоростей в идеальный газ (распределение ци с тремя степенями свободы).

Определения

Функция плотности вероятности

В функция плотности вероятности (pdf) хи-распределения

${ displaystyle f (x; k) = { begin {cases} { dfrac {x ^ {k-1} e ^ {- x ^ {2} / 2}} {2 ^ {k / 2-1} Gamma left ({ frac {k} {2}} right)}}, & x geq 0; 0, & { text {else}}. End {cases}}}$

куда ${ Displaystyle Gamma (г)}$ это гамма-функция.

Кумулятивная функция распределения

Кумулятивная функция распределения определяется как:

${ Displaystyle F (х; к) = п (к / 2, х ^ {2} / 2) ,}$

куда ${ Displaystyle P (к, х)}$ это регуляризованная гамма-функция.

Производящие функции

В момент-производящая функция дан кем-то:

${ Displaystyle M (t) = M left ({ frac {k} {2}}, { frac {1} {2}}, { frac {t ^ {2}} {2}} right ) + t { sqrt {2}} , { frac { Gamma ((k + 1) / 2)} { Gamma (k / 2)}} M left ({ frac {k + 1} {2}}, { frac {3} {2}}, { frac {t ^ {2}} {2}} right),}$

куда ${ Displaystyle М (а, б, г)}$ Куммера конфлюэнтная гипергеометрическая функция. В характеристическая функция дан кем-то:

${ displaystyle varphi (t; k) = M left ({ frac {k} {2}}, { frac {1} {2}}, { frac {-t ^ {2}} {2) }} right) + it { sqrt {2}} , { frac { Gamma ((k + 1) / 2)} { Gamma (k / 2)}} M left ({ frac { k + 1} {2}}, { frac {3} {2}}, { frac {-t ^ {2}} {2}} right).}$

Характеристики

Моменты

Сырье моменты тогда даются:

${ displaystyle mu _ {j} = int _ {0} ^ { infty} f (x; k) x ^ {j} dx = 2 ^ {j / 2} { frac { Gamma ((k + j) / 2)} { Gamma (k / 2)}}}$

куда ${ Displaystyle Gamma (г)}$ это гамма-функция. Итак, первые несколько сырых моментов:

${ displaystyle mu _ {1} = { sqrt {2}} , , { frac { Gamma ((k ! + ! 1) / 2)} { Gamma (k / 2)} }}$

${ Displaystyle му _ {2} = к ,}$

${ Displaystyle му _ {3} = 2 { sqrt {2}} , , { гидроразрыва { Gamma ((k ! + ! 3) / 2)} { Gamma (k / 2) }} = (k + 1) mu _ {1}}$

${ Displaystyle му _ {4} = (к) (к + 2) ,}$

${ displaystyle mu _ {5} = 4 { sqrt {2}} , , { frac { Gamma ((k ! + ! 5) / 2)} { Gamma (k / 2) }} = (k + 1) (k + 3) mu _ {1}}$

${ Displaystyle му _ {6} = (к) (к + 2) (к + 4) ,}$

где крайние правые выражения получены с использованием повторяющегося отношения для гамма-функции:

${ Displaystyle Гамма (х + 1) = х Гамма (х) ,}$

Из этих выражений мы можем вывести следующие отношения:

Иметь в виду: ${ displaystyle mu = { sqrt {2}} , , { frac { Gamma ((k + 1) / 2)} { Gamma (k / 2)}}}$

Разница: ${ Displaystyle V = к- му ^ {2} ,}$

Асимметрия: ${ displaystyle gamma _ {1} = { frac { mu} { sigma ^ {3}}} , (1-2 sigma ^ {2})}$

Превышение эксцесса: ${ displaystyle gamma _ {2} = { frac {2} { sigma ^ {2}}} (1- mu sigma gamma _ {1} - sigma ^ {2})}$

Энтропия

Энтропия определяется как:

${ Displaystyle S = ln ( Gamma (k / 2)) + { frac {1} {2}} (k ! - ! ln (2) ! - ! (k ! - ! 1) psi ^ {0} (k / 2))}$

куда ${ Displaystyle psi ^ {0} (г)}$ это полигамма функция.

Большое n-приближение

Мы находим большое n = k + 1 приближение среднего и дисперсии распределения chi. Это имеет приложение, например при нахождении распределения стандартного отклонения выборки из нормально распределенной совокупности, где n - размер выборки.

Тогда среднее значение:

${ displaystyle mu = { sqrt {2}} , , { frac { Gamma (n / 2)} { Gamma ((n-1) / 2)}}}$

Мы используем Формула дублирования Лежандра написать:

${ Displaystyle 2 ^ {п-2} , Гамма ((п-1) / 2) cdot Гамма (п / 2) = { sqrt { pi}} Гамма (п-1)}$,

так что:

${ displaystyle mu = { sqrt {2 / pi}} , 2 ^ {n-2} , { frac {( Gamma (n / 2)) ^ {2}} { Gamma (n -1)}}}$

С помощью Приближение Стирлинга для гамма-функции мы получаем следующее выражение для среднего:

${ displaystyle mu = { sqrt {2 / pi}} , 2 ^ {n-2} , { frac { left ({ sqrt {2 pi}} (n / 2-1) ^ {n / 2-1 + 1/2} e ^ {- (n / 2-1)} cdot [1 + { frac {1} {12 (n / 2-1)}} + O ({ frac {1} {n ^ {2}}})] right) ^ {2}} {{ sqrt {2 pi}} (n-2) ^ {n-2 + 1/2} e ^ {- (n-2)} cdot [1 + { frac {1} {12 (n-2)}} + O ({ frac {1} {n ^ {2}}})]}}}$

${ displaystyle = (n-2) ^ {1/2} , cdot left [1 + { frac {1} {4n}} + O ({ frac {1} {n ^ {2}}) }) right] = { sqrt {n-1}} , (1 - { frac {1} {n-1}}) ^ {1/2} cdot left [1 + { frac { 1} {4n}} + O ({ frac {1} {n ^ {2}}}) right]}$

${ displaystyle = { sqrt {n-1}} , cdot left [1 - { frac {1} {2n}} + O ({ frac {1} {n ^ {2}}}) right] , cdot left [1 + { frac {1} {4n}} + O ({ frac {1} {n ^ {2}}}) right]}$

${ displaystyle = { sqrt {n-1}} , cdot left [1 - { frac {1} {4n}} + O ({ frac {1} {n ^ {2}}}) верно]}$

Таким образом, разница составляет:

${ displaystyle V = (n-1) - mu ^ {2} , = (n-1) cdot { frac {1} {2n}} , cdot left [1 + O ({ frac {1} {n}}) right]}$

Связанные дистрибутивы

• Если ${ displaystyle X sim chi _ {k}}$ тогда ${ Displaystyle X ^ {2} sim chi _ {k} ^ {2}}$ (распределение хи-квадрат )
• ${ displaystyle lim _ {k to infty} { tfrac { chi _ {k} - mu _ {k}} { sigma _ {k}}} { xrightarrow {d}} N ( 0,1) ,}$ (Нормальное распределение )
• Если ${ Displaystyle Х сим N (0,1) ,}$ тогда ${ Displaystyle | Икс | сим чи _ {1} ,}$
• Если ${ Displaystyle Х сим чи _ {1} ,}$ тогда ${ Displaystyle сигма Икс сим HN ( сигма) ,}$ (полунормальное распределение ) для любого ${ displaystyle sigma> 0 ,}$
• ${ displaystyle chi _ {2} sim mathrm {Rayleigh} (1) ,}$ (Распределение Рэлея )
• ${ Displaystyle чи _ {3} сим mathrm {Максвелл} (1) ,}$ (Распределение Максвелла )
• ${ Displaystyle | { boldsymbol {N}} _ {я = 1, ldots, k} {(0,1)} | _ {2} sim chi _ {k}}$ (The 2-норма из ${ displaystyle k}$ стандартные нормально распределенные переменные - это распределение хи с ${ displaystyle k}$ степени свободы )
• Распределение чи - это частный случай обобщенное гамма-распределение или Распределение Накагами или нецентральное распределение ци
• Среднее значение распределения хи (масштабируется на квадратный корень из ${ displaystyle n-1}$) дает поправочный коэффициент в несмещенная оценка стандартного отклонения нормального распределения.

Различные распределения хи и хи-квадрат

Имя	Статистика
распределение хи-квадрат	${ displaystyle sum _ {я = 1} ^ {k} left ({ frac {X_ {i} - mu _ {i}} { sigma _ {i}}} right) ^ {2} }$
нецентральное распределение хи-квадрат	${ displaystyle sum _ {я = 1} ^ {k} left ({ frac {X_ {i}} { sigma _ {i}}} right) ^ {2}}$
распределение ци	${ displaystyle { sqrt { sum _ {i = 1} ^ {k} left ({ frac {X_ {i} - mu _ {i}} { sigma _ {i}}} right) ^ {2}}}}$
нецентральное распределение ци	${ displaystyle { sqrt { sum _ {я = 1} ^ {k} left ({ frac {X_ {i}} { sigma _ {i}}} right) ^ {2}}}}$

Смотрите также

• Распределение Накагами

Рекомендации

• Марта Л. Абелл, Джеймс П. Брэсселтон, Джон Артур Рэфтер, Джон А. Рэфтер, Статистика с помощью Mathematica (1999), 237f.
• Ян В. Гуч, Энциклопедический словарь полимеров т. 1 (2010 г.), Приложение E, п. 972.

внешняя ссылка

• http://mathworld.wolfram.com/ChiDistribution.html