Логит-нормальное распределение - Logit-normal distribution

Логит-нормальный

Функция плотности вероятности
Кумулятивная функция распределения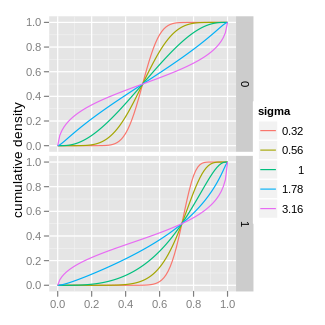
Обозначение	${ Displaystyle Р ({ mathcal {N}} ( му, , sigma ^ {2}))}$
Параметры	σ2 > 0 - шкала в квадрате (реальная), μ ∈ р - место расположения
Поддерживать	Икс ∈ (0, 1)
PDF	${ displaystyle { frac {1} { sigma { sqrt {2 pi}}}} , e ^ {- { frac {( operatorname {logit} (x) - mu) ^ {2} } {2 sigma ^ {2}}}} { frac {1} {x (1-x)}}}$
CDF	${ displaystyle { frac {1} {2}} { Big [} 1+ operatorname {erf} { Big (} { frac { operatorname {logit} (x) - mu} { sqrt { 2 sigma ^ {2}}}} { Big)} { Big]}}$
Иметь в виду	нет аналитического решения
Медиана	${ Displaystyle Р ( му) ,}$
Режим	нет аналитического решения
Дисперсия	нет аналитического решения
MGF	нет аналитического решения

В теория вероятности, а логит-нормальное распределение это распределение вероятностей из случайная переменная чей логит имеет нормальное распределение. Если Y - случайная величина с нормальным распределением, а п это стандарт логистическая функция, тогда Икс = п(Y) имеет логит-нормальное распределение; аналогично, если Икс логит-нормально распределен, то Y = логит (Икс) = журнал (Икс/(1-Икс)) нормально раздается. Он также известен как логистическое нормальное распределение,^[1] что часто относится к полиномиальной версии логита (например,^[2][3][4][5]).

Переменная может быть смоделирована как логит-нормальная, если это пропорция, которая ограничена нулем и единицей и где значения нуля и единицы никогда не встречаются.

Характеристика

Функция плотности вероятности

В функция плотности вероятности (PDF) логит-нормального распределения для 0 ≤ Икс ≤ 1, составляет:

${ displaystyle f_ {X} (x; mu, sigma) = { frac {1} { sigma { sqrt {2 pi}}}} , { frac {1} {x (1- x)}} , e ^ {- { frac {( operatorname {logit} (x) - mu) ^ {2}} {2 sigma ^ {2}}}}}$

куда μ и σ являются иметь в виду и стандартное отклонение переменной логит (по определению логит переменной является нормально распределенным).

Плотность, полученная изменением знака μ симметричен в том смысле, что он равен f (1-x; -μ,σ), смещая режим на другую сторону 0,5 (середина интервала (0,1)).

График Logitnormal PDF для различных комбинаций μ (грани) и σ (цвета)

Моменты

Моменты логит-нормального распределения не имеют аналитического решения. Моменты можно оценить по численное интегрирование, однако численное интегрирование может оказаться недопустимым, когда значения ${ textstyle mu, sigma ^ {2}}$таковы, что функция плотности расходится до бесконечности в конечных точках нуль и единица. Альтернативой является использование наблюдения, что логит-нормаль является преобразованием нормальной случайной величины. Это позволяет нам аппроксимировать моменты с помощью следующей квази Монте-Карло оценки ${ displaystyle E [X ^ {n}] приблизительно { frac {1} {K-1}} sum _ {i = 1} ^ {K-1} left (P left ( Phi _ { mu, sigma ^ {2}} ^ {- 1} (i / K) right) right) ^ {n},}$

куда ${ textstyle P}$ стандартная логистическая функция, и ${ textstyle Phi _ { mu, sigma ^ {2}} ^ {- 1}}$ - обратная кумулятивная функция распределения нормального распределения со средним значением и дисперсией ${ textstyle mu, sigma ^ {2}}$.

Режим или режимы

Когда производная плотности равна 0, то положение моды x удовлетворяет следующему уравнению:

${ displaystyle operatorname {logit} (x) = sigma ^ {2} (2x-1) + mu.}$

Для некоторых значений параметров есть два решения, т.е. распределение бимодальный.

Многомерное обобщение

В логистическое нормальное распределение является обобщением логит-нормального распределения на D-мерные векторы вероятностей путем логистического преобразования многомерного нормального распределения.^[6][7][8]

Функция плотности вероятности

В функция плотности вероятности является:

${ displaystyle f_ {X} ( mathbf {x}; { boldsymbol { mu}}, { boldsymbol { Sigma}}) = { frac {1} {| 2 pi { boldsymbol { Sigma }} | ^ { frac {1} {2}}}} , { frac {1} { prod limits _ {i = 1} ^ {D} x_ {i}}} , e ^ { - { frac {1} {2}} left { log left ({ frac { mathbf {x} _ {- D}} {x_ {D}}} right) - { boldsymbol { mu}} right } ^ { top} { boldsymbol { Sigma}} ^ {- 1} left { log left ({ frac { mathbf {x} _ {- D}} {x_ {D}}} right) - { boldsymbol { mu}} right }} quad, quad mathbf {x} in { mathcal {S}} ^ {D} ; ;,}$

куда ${ displaystyle mathbf {x} _ {- D}}$ обозначает вектор первых (D-1) компонент ${ displaystyle mathbf {x}}$ и ${ Displaystyle { mathcal {S}} ^ {D}}$ обозначает симплекс D-мерных векторов вероятностей. Это следует из применения аддитивная логистическая трансформация нанести на карту многомерный нормальный случайная переменная ${ displaystyle mathbf {y} sim { mathcal {N}} left ({ boldsymbol { mu}}, { boldsymbol { Sigma}} right) ;, ; mathbf {y} in mathbb {R} ^ {D-1}}$ в симплекс:

${ displaystyle mathbf {x} = left [{ frac {e ^ {y_ {1}}} {1+ sum _ {i = 1} ^ {D-1} e ^ {y_ {i}}] }}, dots, { frac {e ^ {y_ {D-1}}} {1+ sum _ {i = 1} ^ {D-1} e ^ {y_ {i}}}}, { frac {1} {1+ sum _ {i = 1} ^ {D-1} e ^ {y_ {i}}}} right] ^ { top}}$

Гауссовы функции плотности и соответствующие логистические нормальные функции плотности после логистического преобразования.

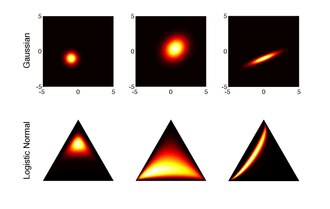
Уникальное обратное отображение определяется выражением:

${ displaystyle mathbf {y} = left [ log left ({ frac {x_ {1}} {x_ {D}}} right), dots, log left ({ frac {x_ {D-1}} {x_ {D}}} right) right] ^ { top}}$.

Это случай вектора Икс какие компоненты в сумме составляют один. В случае Икс с сигмоидальными элементами, то есть когда

${ displaystyle mathbf {y} = left [ log left ({ frac {x_ {1}} {1-x_ {1}}} right), dots, log left ({ frac {x_ {D}} {1-x_ {D}}} right) right] ^ { top}}$

у нас есть

${ displaystyle f_ {X} ( mathbf {x}; { boldsymbol { mu}}, { boldsymbol { Sigma}}) = { frac {1} {| 2 pi { boldsymbol { Sigma }} | ^ { frac {1} {2}}}} , { frac {1} { prod limits _ {i = 1} ^ {D} left (x_ {i} (1-x_ {i}) right)}} , e ^ {- { frac {1} {2}} left { log left ({ frac { mathbf {x}} {1- mathbf { x}}} right) - { boldsymbol { mu}} right } ^ { top} { boldsymbol { Sigma}} ^ {- 1} left { log left ({ frac { mathbf {x}} {1- mathbf {x}}} right) - { boldsymbol { mu}} right }}}$

где бревно и деление в аргументе берутся поэлементно. Это связано с тем, что матрица Якоби преобразования диагональна с элементами ${ displaystyle { frac {1} {x_ {i} (1-x_ {i})}}}$.

Использование в статистическом анализе

Логистическое нормальное распределение - более гибкая альтернатива Распределение Дирихле в том, что он может фиксировать корреляции между компонентами векторов вероятности. Он также может упростить статистический анализ композиционные данные позволяя ответить на вопросы о логарифмических отношениях компонентов векторов данных. Часто интересуют скорее отношения, чем абсолютные значения компонентов.

Симплекс вероятности представляет собой ограниченное пространство, что делает стандартные методы, которые обычно применяются к векторам в ${ Displaystyle mathbb {R} ^ {п}}$ менее значимый. Aitchison описал проблему ложных отрицательных корреляций при применении таких методов непосредственно к симплициальным векторам.^[7] Однако отображение композиционных данных в ${ Displaystyle { mathcal {S}} ^ {D}}$ через инверсию аддитивного логистического преобразования дает действительные данные в ${ Displaystyle mathbb {R} ^ {D-1}}$. К этому представлению данных можно применить стандартные методы. Такой подход оправдывает использование логистического нормального распределения, которое, таким образом, можно рассматривать как «гауссовский симплекс».

Связь с распределением Дирихле

Логистическая нормальная аппроксимация распределения Дирихле

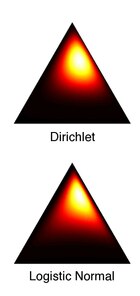
В Дирихле а логистические нормальные распределения никогда не могут быть в точности равными при любом выборе параметров. Однако Эйчисон описал метод аппроксимации Дирихле логистической нормалью, так что их Дивергенция Кульбака – Лейблера (KL) сводится к минимуму:

${ Displaystyle К (p, q) = int _ { mathcal {S}} ^ {D}} p left ( mathbf {x} mid { boldsymbol { alpha}} right) log left ({ frac {p left ( mathbf {x} mid { boldsymbol { alpha}} right)} {q left ( mathbf {x} mid { boldsymbol { mu}}) , { boldsymbol { Sigma}} right)}} right) , d mathbf {x}}$

Это сводится к минимуму:

${ displaystyle { boldsymbol { mu}} ^ {*} = mathbf {E} _ {p} left [ log left ({ frac { mathbf {x} _ {- D}} {x_ {D}}} right) right] quad, quad { boldsymbol { Sigma}} ^ {*} = { textbf {Var}} _ {p} left [ log left ({ frac { mathbf {x} _ {- D}} {x_ {D}}} right) right]}$

Используя моментные свойства распределения Дирихле, решение можно записать в терминах дигамма ${ displaystyle psi}$ и тригамма ${ displaystyle psi '}$ функции:

${ Displaystyle му _ {я} ^ {*} = psi left ( alpha _ {i} right) - psi left ( alpha _ {D} right) quad, quad i = 1, ldots, D-1}$

${ Displaystyle Sigma _ {ii} ^ {*} = psi ' left ( alpha _ {i} right) + psi' left ( alpha _ {D} right) quad, quad я = 1, ldots, D-1}$

${ Displaystyle Sigma _ {ij} ^ {*} = psi ' left ( alpha _ {D} right) quad, quad i neq j}$

Это приближение особенно точно для больших ${ displaystyle { boldsymbol { alpha}}}$. Фактически, можно показать, что для ${ Displaystyle альфа _ {я} rightarrow infty, я = 1, ldots, D}$у нас есть это ${ displaystyle p left ( mathbf {x} mid { boldsymbol { alpha}} right) rightarrow q left ( mathbf {x} mid { boldsymbol { mu}} ^ {*} , { boldsymbol { Sigma}} ^ {*} right)}$.

Смотрите также

• Бета-распространение и Распределение Кумарасвами, другие двухпараметрические распределения на ограниченном интервале аналогичной формы

дальнейшее чтение

• Фредерик, П. и Лад, Ф. (2008) Два момента логитнормального распределения. Коммуникации в статистическом моделировании и вычислениях. 37: 1263-1269
• Мид, Р. (1965). «Обобщенное логит-нормальное распределение». Биометрия. 21 (3): 721–732. Дои:10.2307/2528553. JSTOR  2528553.

внешняя ссылка

• пакет logitnorm за р