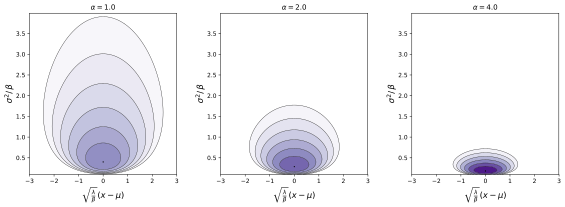
нормальная обратная гамма Функция плотности вероятности
Параметры μ {displaystyle mu,} место расположения (настоящий ) λ > 0 {displaystyle lambda> 0,} α > 0 {displaystyle alpha> 0,} β > 0 {displaystyle eta> 0,} Поддерживать Икс ∈ ( − ∞ , ∞ ) , σ 2 ∈ ( 0 , ∞ ) {displaystyle xin (-infty, infty),!,; sigma ^ {2} in (0, infty)} PDF λ 2 π σ 2 β α Γ ( α ) ( 1 σ 2 ) α + 1 exp ( − 2 β + λ ( Икс − μ ) 2 2 σ 2 ) {displaystyle {frac {sqrt {lambda}} {sqrt {2pi sigma ^ {2}}}} {frac {eta ^ {alpha}} {Gamma (alpha)}} left ({frac {1} {sigma ^ {2 }}} ight) ^ {alpha +1} exp left (- {frac {2 eta + lambda (x-mu) ^ {2}} {2sigma ^ {2}}} ight)} Иметь в виду E [ Икс ] = μ {displaystyle operatorname {E} [x] = mu}
E [ σ 2 ] = β α − 1 {displaystyle operatorname {E} [sigma ^ {2}] = {frac {eta} {alpha -1}}} α > 1 {displaystyle alpha> 1} Режим Икс = μ (одномерный) , Икс = μ (многомерный) {displaystyle x = mu; {extrm {(одномерный)}}, x = {oldsymbol {mu}}; {extrm {(многомерный)}}}
σ 2 = β α + 1 + 1 / 2 (одномерный) , σ 2 = β α + 1 + k / 2 (многомерный) {displaystyle sigma ^ {2} = {frac {eta} {alpha + 1 + 1/2}}; {extrm {(univariate)}}, sigma ^ {2} = {frac {eta} {alpha + 1 + k / 2}}; {extrm {(многовариантный)}}} Дисперсия Вар [ Икс ] = β ( α − 1 ) λ {displaystyle operatorname {Var} [x] = {frac {eta} {(alpha -1) lambda}}} α > 1 {displaystyle alpha> 1} Вар [ σ 2 ] = β 2 ( α − 1 ) 2 ( α − 2 ) {displaystyle operatorname {Var} [sigma ^ {2}] = {frac {eta ^ {2}} {(alpha -1) ^ {2} (alpha -2)}}} α > 2 {displaystyle alpha> 2}
Cov [ Икс , σ 2 ] = 0 {displaystyle operatorname {Cov} [x, sigma ^ {2}] = 0} α > 1 {displaystyle alpha> 1}
В теория вероятности и статистика , то нормальное обратное гамма-распределение (или же Гауссово-обратное гамма-распределение ) является четырехпараметрическим семейством многомерных непрерывных распределения вероятностей . Это сопряженный предшествующий из нормальное распределение с неизвестным иметь в виду и отклонение .
Определение Предполагать
Икс ∣ σ 2 , μ , λ ∼ N ( μ , σ 2 / λ ) {displaystyle xmid sigma ^ {2}, mu, lambda sim mathrm {N} (mu, sigma ^ {2} / lambda) ,!} имеет нормальное распределение с иметь в виду μ {displaystyle mu} отклонение σ 2 / λ {displaystyle sigma ^ {2} / lambda}
σ 2 ∣ α , β ∼ Γ − 1 ( α , β ) {displaystyle sigma ^ {2} mid alpha, eta sim Gamma ^ {- 1} (alpha, eta)!} имеет обратное гамма-распределение . потом ( Икс , σ 2 ) {displaystyle (x, sigma ^ {2})}
( Икс , σ 2 ) ∼ N- Γ − 1 ( μ , λ , α , β ) . {displaystyle (x, sigma ^ {2}) sim {ext {N -}} Gamma ^ {- 1} (mu, lambda, alpha, eta) !.} ( НИГ {displaystyle {ext {NIG}}} N- Γ − 1 . {displaystyle {ext {N -}} Gamma ^ {- 1}.}
В нормальное обратное распределение Вишарта является обобщением нормального-обратного-гамма-распределения, которое определено для многомерных случайных величин.
Характеристика Функция плотности вероятности ж ( Икс , σ 2 ∣ μ , λ , α , β ) = λ σ 2 π β α Γ ( α ) ( 1 σ 2 ) α + 1 exp ( − 2 β + λ ( Икс − μ ) 2 2 σ 2 ) {displaystyle f (x, sigma ^ {2} mid mu, lambda, alpha, eta) = {frac {sqrt {lambda}} {sigma {sqrt {2pi}}}}, {frac {eta ^ {alpha}} { Гамма (альфа)}}, слева ({frac {1} {sigma ^ {2}}} ight) ^ {alpha +1} exp left (- {frac {2 eta + lambda (x-mu) ^ {2} } {2sigma ^ {2}}} ight)} Для многомерной формы, где Икс {displaystyle mathbf {x}} k × 1 {displaystyle k imes 1}
ж ( Икс , σ 2 ∣ μ , V − 1 , α , β ) = | V | − 1 / 2 ( 2 π ) − k / 2 β α Γ ( α ) ( 1 σ 2 ) α + 1 + k / 2 exp ( − 2 β + ( Икс − μ ) ′ V − 1 ( Икс − μ ) 2 σ 2 ) . {displaystyle f (mathbf {x}, sigma ^ {2} mid mu, mathbf {V} ^ {- 1}, alpha, eta) = | mathbf {V} | ^ {- 1/2} {(2pi) ^ {-k / 2}}, {frac {eta ^ {alpha}} {Gamma (alpha)}}, left ({frac {1} {sigma ^ {2}}} ight) ^ {alpha + 1 + k / 2} exp left (- {frac {2 eta + (mathbf {x} - {oldsymbol {mu}}) 'mathbf {V} ^ {- 1} (mathbf {x} - {oldsymbol {mu}})} { 2sigma ^ {2}}} ight).} куда | V | {displaystyle | mathbf {V} |} детерминант из k × k {displaystyle k imes k} матрица V {displaystyle mathbf {V}} k = 1 {displaystyle k = 1} Икс , V , μ {displaystyle mathbf {x}, mathbf {V}, {oldsymbol {mu}}} скаляры .
Альтернативная параметризация Также возможно позволить γ = 1 / λ {displaystyle gamma = 1 / lambda}
ж ( Икс , σ 2 ∣ μ , γ , α , β ) = 1 σ 2 π γ β α Γ ( α ) ( 1 σ 2 ) α + 1 exp ( − 2 γ β + ( Икс − μ ) 2 2 γ σ 2 ) {displaystyle f (x, sigma ^ {2} mid mu, gamma, alpha, eta) = {frac {1} {sigma {sqrt {2pi gamma}}}}, {frac {eta ^ {alpha}} {Gamma ( alpha)}}, left ({frac {1} {sigma ^ {2}}} ight) ^ {alpha +1} exp left (- {frac {2gamma eta + (x-mu) ^ {2}} {2gamma сигма ^ {2}}} ight)} В многомерной форме соответствующим изменением будет учет ковариационной матрицы V {displaystyle mathbf {V}} обратный V − 1 {displaystyle mathbf {V} ^ {- 1}}
Кумулятивная функция распределения F ( Икс , σ 2 ∣ μ , λ , α , β ) = е − β σ 2 ( β σ 2 ) α ( Эрф ( λ ( Икс − μ ) 2 σ ) + 1 ) 2 σ 2 Γ ( α ) {displaystyle F (x, sigma ^ {2} mid mu, lambda, alpha, eta) = {frac {e ^ {- {frac {eta} {sigma ^ {2}}}} влево ({frac {eta} { sigma ^ {2}}} ight) ^ {alpha} left (имя оператора {erf} left ({frac {{sqrt {lambda}} (x-mu)} {{sqrt {2}} sigma}} ight) + 1ight) )} {2sigma ^ {2} Гамма (альфа)}}} Характеристики Маржинальные распределения Данный ( Икс , σ 2 ) ∼ N- Γ − 1 ( μ , λ , α , β ) . {displaystyle (x, sigma ^ {2}) sim {ext {N -}} Gamma ^ {- 1} (mu, lambda, alpha, eta) !.} σ 2 {displaystyle sigma ^ {2}} обратное гамма-распределение :
σ 2 ∼ Γ − 1 ( α , β ) {displaystyle sigma ^ {2} sim Gamma ^ {- 1} (alpha, eta)!} пока α λ β ( Икс − μ ) {displaystyle {sqrt {frac {alpha lambda} {eta}}} (x-mu)} t распределение с 2 α {displaystyle 2alpha}
В многомерном случае предельное распределение Икс {displaystyle mathbf {x}} многомерное t-распределение :
Икс ∼ т 2 α ( μ , β α V − 1 ) {displaystyle mathbf {x} sim t_ {2alpha} ({oldsymbol {mu}}, {frac {eta} {alpha}} mathbf {V} ^ {- 1})!} Суммирование Масштабирование Экспоненциальная семья Информационная энтропия Дивергенция Кульбака – Лейблера Оценка максимального правдоподобия Апостериорное распределение параметров См. Статьи на нормальное гамма-распределение и сопряженный предшествующий .
Интерпретация параметров См. Статьи на нормальное гамма-распределение и сопряженный предшествующий .
Генерация случайных величин нормальной-обратной-гамма Генерация случайных величин проста:
Образец σ 2 {displaystyle sigma ^ {2}} α {displaystyle alpha} β {displaystyle eta} Образец Икс {displaystyle x} μ {displaystyle mu} σ 2 / λ {displaystyle sigma ^ {2} / lambda} Связанные дистрибутивы В нормальное гамма-распределение такое же распределение, параметризованное точность скорее, чем отклонение Обобщение этого распределения, которое учитывает многомерное среднее и полностью неизвестную положительно-определенную матрицу ковариаций. σ 2 V {displaystyle sigma ^ {2} mathbf {V}} σ 2 {displaystyle sigma ^ {2}} нормальное обратное распределение Вишарта Смотрите также Рекомендации Денисон, Дэвид Г. Т.; Холмс, Кристофер С .; Маллик, Бани К .; Смит, Адриан Ф. М. (2002) Байесовские методы нелинейной классификации и регрессии , Wiley. ISBN 0471490369 Кох, Карл-Рудольф (2007) Введение в байесовскую статистику (2-е издание), Springer. ISBN 354072723X Дискретный одномерный Дискретный одномерный Непрерывный одномерный Непрерывный одномерный Непрерывный одномерный Непрерывный одномерный Смешанная непрерывно-дискретная одномерная Многовариантный (совместный) Направленный Вырожденный и единственное число Семьи







![{displaystyle operatorname {E} [x] = mu}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d60f5921cca1c75d673eb70db395bf3a88f9170f)
![{displaystyle operatorname {E} [sigma ^ {2}] = {frac {eta} {alpha -1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b74baba053fd81d56d62de618558ac7af62ade55)



![{displaystyle operatorname {Var} [x] = {frac {eta} {(alpha -1) lambda}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c11eddb529a936912263edfb0c46ce2a42adfbd5)
![{displaystyle operatorname {Var} [sigma ^ {2}] = {frac {eta ^ {2}} {(alpha -1) ^ {2} (alpha -2)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d089f3b7da4ce1f13940b4731eb531932850d0e)

![{displaystyle operatorname {Cov} [x, sigma ^ {2}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7006f5738ee174c6c35e1694f1c4ac3b2c9c42)





























