Распределение Гомперца - Википедия - Gompertz distribution

Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. Пожалуйста, помогите улучшать эта статья введение более точные цитаты. (Декабрь 2011 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Распределение Гомперца

Функция плотности вероятности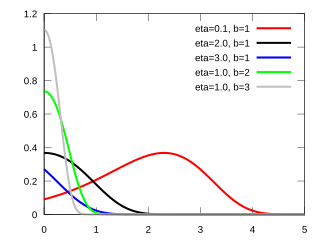
Кумулятивная функция распределения
Параметры	форма ${ displaystyle eta> 0 , !}$, шкала ${ displaystyle b> 0 , !}$
Поддерживать	${ Displaystyle х в [0, infty) !}$
PDF	${ displaystyle b eta exp left ( eta + bx- eta e ^ {bx} right)}$
CDF	${ Displaystyle 1- ехр влево (- эта влево (е ^ {bx} -1 вправо) вправо)}$
Иметь в виду	${ displaystyle (1 / b) e ^ { eta} { text {Ei}} left (- eta right)}$ ${ displaystyle { text {где Ei}} left (z right) = int limits _ {- z} ^ { infty} left (e ^ {- v} / v right) dv}$
Медиана	${ Displaystyle влево (1 / б вправо) пер влево [ влево (-1 / эта вправо) пер влево (1/2 вправо) +1 вправо]}$
Режим	${ Displaystyle = влево (1 / Ь вправо) пер влево (1 / эта вправо) }$ ${ displaystyle { text {with}} 0 <{ text {F}} left (x ^ {*} right) <1-e ^ {- 1} = 0,632121,0 < eta <1}$ ${ Displaystyle = 0, quad eta geq 1}$
Дисперсия	${ displaystyle left (1 / b right) ^ {2} e ^ { eta} {- 2 eta {} _ {3} { text {F}} _ {3} left (1 , 1,1; 2,2,2; - eta right) + gamma ^ {2}}$${ Displaystyle + влево ( пи ^ {2} / 6 вправо) +2 гамма пер влево ( эта право) + [ пер влево ( эта вправо)] ^ {2} - e ^ { eta} [{ text {Ei}} left (- eta right)] ^ {2} }}$ ${ displaystyle { begin {align} { text {where}} & gamma { text {- постоянная Эйлера:}} , ! & gamma = - psi left (1 right) = { text {0,577215 ...}} end {выровнено}}}$${ displaystyle { begin {align} { text {and}} {} _ {3} { text {F}} _ {3} & left (1,1,1; 2,2,2; - z right) = & sum _ {k = 0} ^ { infty} left [1 / left (k + 1 right) ^ {3} right] left (-1 right) ^ {k} left (z ^ {k} / k! right) end {выровнено}}}$
MGF	${ displaystyle { text {E}} left (e ^ {- tx} right) = eta e ^ { eta} { text {E}} _ {t / b} left ( eta верно)}$ ${ displaystyle { text {с E}} _ {t / b} left ( eta right) = int _ {1} ^ { infty} e ^ {- eta v} v ^ {- t / b} dv, t> 0}$

В вероятность и статистика, то Распределение Гомперца это непрерывное распределение вероятностей, названный в честь Бенджамин Гомпертц. Распределение Гомпертца часто применяется для описания распределения продолжительности жизни взрослых людей по демографы^[1][2] и актуарии.^[3][4] Связанные области науки, такие как биология^[5] и геронтология^[6] также рассматривали распределение Гомперца для анализа выживаемости. Совсем недавно компьютерные ученые также начали моделировать частоту отказов компьютерного кода с помощью распределения Гомпертца.^[7] В маркетинговой науке он использовался как моделирование на индивидуальном уровне для Значение жизни клиентов моделирование.^[8] В теория сети, особенно Модель Эрдеша – Реньи, длина прогулки случайного самопроизвольная прогулка (SAW) распределяется по распределению Гомпертца.^[9]

Технические характеристики

Функция плотности вероятности

В функция плотности вероятности распределения Гомперца:

${ Displaystyle е влево (х; эта, б право) = б эта ехр влево ( эта + bx- эта е ^ {bx} право) { текст {для}} х geq 0, ,}$

куда ${ displaystyle b> 0 , !}$ это параметр масштаба и ${ displaystyle eta> 0 , !}$ это параметр формы распределения Гомперца. В актуарных и биологических науках, а также в демографии распределение Гомперца параметризуется несколько иначе (Закон смертности Гомперца-Мейкхема ).

Кумулятивная функция распределения

В кумулятивная функция распределения распределения Гомперца:

${ displaystyle F left (x; eta, b right) = 1- exp left (- eta left (e ^ {bx} -1 right) right),}$

куда ${ displaystyle eta, b> 0,}$ и ${ Displaystyle х geq 0 ,.}$

Функция создания момента

Функция, производящая момент:

${ displaystyle { text {E}} left (e ^ {- tX} right) = eta e ^ { eta} { text {E}} _ {t / b} left ( eta верно)}$

куда

${ displaystyle { text {E}} _ {t / b} left ( eta right) = int _ {1} ^ { infty} e ^ {- eta v} v ^ {- t / b} dv, t> 0.}$

Характеристики

Распределение Гомперца - это гибкое распределение, которое можно наклонять вправо и влево. Его функция опасности ${ displaystyle h (x) = eta be ^ {bx}}$ является выпуклой функцией от ${ displaystyle F left (x; eta, b right)}$. Модель может быть вписана в парадигму имитации инноваций с помощью ${ displaystyle p = eta b}$ как коэффициент инновационности и ${ displaystyle b}$ как коэффициент имитации. Когда ${ displaystyle t}$ становится большим, ${ Displaystyle г (т)}$ подходы ${ displaystyle infty}$. Модель также может принадлежать к парадигме склонности к принятию с ${ displaystyle eta}$ как склонность к усыновлению и ${ displaystyle b}$ как общая привлекательность нового предложения.

Формы

Функция плотности Гомперца может принимать разные формы в зависимости от значений параметра формы. ${ displaystyle eta , !}$:

• Когда ${ displaystyle eta geq 1, ,}$ функция плотности вероятности имеет режим 0.
• Когда ${ Displaystyle 0 < eta <1, ,}$ функция плотности вероятности имеет режим при

${ displaystyle x ^ {*} = left (1 / b right) ln left (1 / eta right) { text {with}} 0$

Расхождение Кульбака-Лейблера

Если ${ displaystyle f_ {1}}$ и ${ displaystyle f_ {2}}$ являются функциями плотности вероятности двух распределений Гомперца, то их Расхождение Кульбака-Лейблера дан кем-то

${ displaystyle { begin {align} D_ {KL} (f_ {1} parallel f_ {2}) & = int _ {0} ^ { infty} f_ {1} (x; b_ {1}, eta _ {1}) , ln { frac {f_ {1} (x; b_ {1}, eta _ {1})} {f_ {2} (x; b_ {2}, eta _ {2})}} dx & = ln { frac {e ^ { eta _ {1}} , b_ {1} , eta _ {1}} {e ^ { eta _ {2}} , b_ {2} , eta _ {2}}} + e ^ { eta _ {1}} left [ left ({ frac {b_ {2}} {b_ {1 }}} - 1 right) , operatorname {Ei} (- eta _ {1}) + { frac { eta _ {2}} { eta _ {1} ^ { frac {b_ { 2}} {b_ {1}}}}} , Gamma left ({ frac {b_ {2}} {b_ {1}}} + 1, eta _ {1} right) right] - ( eta _ {1} +1) end {align}}}$

куда ${ Displaystyle OperatorName {Ei} ( cdot)}$ обозначает экспоненциальный интеграл и ${ Displaystyle Гамма ( cdot, cdot)}$ это верхний неполная гамма-функция.^[10]

Связанные дистрибутивы

• Если Икс определяется как результат выборки из Гамбель раздача до отрицательного значения Y производится, и установка Икс=−Y, тогда Икс имеет распределение Гомперца.
• В гамма-распределение это естественный сопряженный предшествующий до вероятности Гомперца с известным параметром масштаба ${ displaystyle b , !.}$^[8]
• Когда ${ displaystyle eta , !}$ варьируется в зависимости от гамма-распределение с параметром формы ${ Displaystyle альфа , !}$ и масштабный параметр ${ Displaystyle бета , !}$ (среднее = ${ Displaystyle альфа / бета , !}$), распределение ${ displaystyle x}$ это Гамма / Гомпертц.^[8]

Распределение Гомперца соответствует максимальному месячному количеству осадков за 1 день ^[11]

Приложения

• В гидрология распределение Гомперца применяется к экстремальным явлениям, таким как годовые максимальные однодневные осадки и сток рек. На синем рисунке показан пример подгонки распределения Гомпертца к ранжированным годовым максимальным однодневным осадкам, показывающий также 90% пояс уверенности на основе биномиальное распределение. Данные об осадках представлены построение позиций как часть совокупный частотный анализ.

Смотрите также

• Закон смертности Гомперца-Мейкхема
• Функция Гомперца
• Значение жизни клиентов
• Гамма-распределение Гомперца

Примечания

Рекомендации

• Bemmaor, Albert C .; Глади, Николас (2011). «Реализация модели Gamma / Gompertz / NBD в MATLAB» (PDF). Сержи-Понтуаз: Бизнес-школа ESSEC.^{[постоянная мертвая ссылка ]}
• Гомпертц, Б. (1825). «О природе функции, выражающей закон человеческой смертности, и о новом способе определения ценности жизненных обстоятельств». Философские труды Лондонского королевского общества. 115: 513–583. Дои:10.1098 / рстл.1825.0026. JSTOR  107756.
• Джонсон, Норман Л .; Коц, Самуэль; Балакришнан, Н. (1995). Непрерывные одномерные распределения. 2 (2-е изд.). Нью-Йорк: Джон Вили и сыновья. С. 25–26. ISBN  0-471-58494-0.
• Шейх, А.К .; Boah, J. K .; Юнас, М. (1989). «Усеченная модель экстремальных значений для надежности трубопроводов». Техника надежности и системная безопасность. 25 (1): 1–14. Дои:10.1016/0951-8320(89)90020-3.