Обернутое экспоненциальное распределение - Wrapped exponential distribution

Обернутая экспонента

Функция плотности вероятности 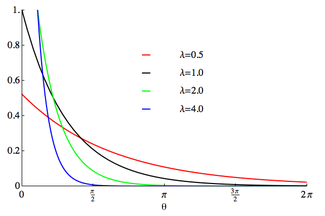Опора выбрана равной [0,2π]
Кумулятивная функция распределения Опора выбрана равной [0,2π]
Параметры	${ displaystyle lambda> 0}$
Поддерживать	${ Displaystyle 0 Leq theta <2 pi}$
PDF	${ displaystyle { frac { lambda e ^ {- lambda theta}} {1-e ^ {- 2 pi lambda}}}}$
CDF	${ displaystyle { frac {1-e ^ {- lambda theta}} {1-e ^ {- 2 pi lambda}}}}}$
Иметь в виду	${ Displaystyle arctan (1 / лямбда)}$ (круговой)
Дисперсия	${ displaystyle 1 - { frac { lambda} { sqrt {1+ lambda ^ {2}}}}}$ (круговой)
Энтропия	${ displaystyle 1+ ln left ({ frac { beta -1} { lambda}} right) - { frac { beta} { beta -1}} ln ( beta)}$ куда ${ Displaystyle бета = е ^ {2 пи лямбда}}$ (дифференциал)
CF	${ displaystyle { frac {1} {1 дюйм / lambda}}}$

В теория вероятности и направленная статистика, а экспоненциальное распределение в оболочке это свернутое распределение вероятностей что является результатом "упаковки" экспоненциальное распределение вокруг единичный круг.

Определение

В функция плотности вероятности свернутого экспоненциального распределения^[1]

${ displaystyle f_ {WE} ( theta; lambda) = sum _ {k = 0} ^ { infty} lambda e ^ {- lambda ( theta +2 pi k)} = { frac { lambda e ^ {- lambda theta}} {1-e ^ {- 2 pi lambda}}},}$

за ${ Displaystyle 0 Leq theta <2 pi}$ куда ${ displaystyle lambda> 0}$ - параметр скорости развернутого распределения. Это идентично усеченное распределение полученные путем ограничения наблюдаемых значений Икс от экспоненциальное распределение с параметром скорости λ к диапазону ${ Displaystyle 0 Leq Икс <2 pi}$.

Характеристическая функция

В характеристическая функция завернутой экспоненты - это просто характеристическая функция экспоненциальной функции, вычисляемая при целочисленных аргументах:

${ displaystyle varphi _ {n} ( lambda) = { frac {1} {1 дюйм / lambda}}}$

что дает альтернативное выражение для упакованной экспоненциальной PDF в терминах круговой переменной г = е ^{я (θ-м)} действительно для всех действительных θ и m:

${ displaystyle { begin {align} f_ {WE} (z; lambda) & = { frac {1} {2 pi}} sum _ {n = - infty} ^ { infty} { frac {z ^ {- n}} {1 дюйм / lambda}} [10pt] & = { begin {cases} { frac { lambda} { pi}} , { textrm {Im }} ( Phi (z, 1, -i lambda)) - { frac {1} {2 pi}} & { text {if}} z neq 1 [12pt] { frac { lambda} {1-e ^ {- 2 pi lambda}}} & { text {if}} z = 1 end {case}} end {выровнено}}}$

куда ${ Displaystyle Phi ()}$ это Лерх трансцендентный функция.

Круговые моменты

В терминах круговой переменной ${ Displaystyle г = е ^ {я тета}}$ Круговые моменты свернутого экспоненциального распределения являются характеристической функцией экспоненциального распределения, оцениваемой при целочисленных аргументах:

${ displaystyle langle z ^ {n} rangle = int _ { Gamma} e ^ {in theta} , f_ {WE} ( theta; lambda) , d theta = { frac { 1} {1 дюйм / lambda}},}$

куда ${ displaystyle Gamma ,}$ это некоторый интервал длины ${ displaystyle 2 pi}$. Тогда первый момент - это среднее значение z, также известный как средний результирующий или средний результирующий вектор:

${ displaystyle langle z rangle = { frac {1} {1-i / lambda}}.}$

Средний угол

${ displaystyle langle theta rangle = mathrm {Arg} langle z rangle = arctan (1 / lambda),}$

а длина среднего результата равна

${ displaystyle R = | langle z rangle | = { frac { lambda} { sqrt {1+ lambda ^ {2}}}}.}.$

и тогда дисперсия равна 1-р.

Характеристика

Обернутое экспоненциальное распределение - это распределение вероятностей максимальной энтропии для дистрибутивов, ограниченных диапазоном ${ Displaystyle 0 Leq theta <2 pi}$ при фиксированном значении ожидания ${ displaystyle operatorname {E} ( theta)}$.^[1]

Смотрите также

• Распространение в оболочке
• Направленная статистика

Рекомендации