Распределение риса - Википедия - Rice distribution

В 2D-плоскости выберите фиксированную точку на расстоянии ν от происхождения. Создайте распределение 2D-точек с центром в этой точке, где Икс и у координаты выбираются независимо от Гауссово распределение со стандартным отклонением σ (синяя область). Если р - расстояние от этих точек до начала координат, тогда р имеет распределение риса.

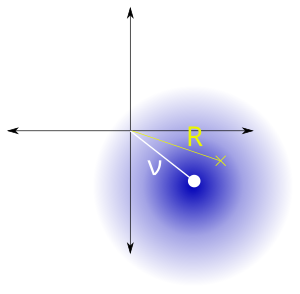
Функция плотности вероятности
Кумулятивная функция распределения
Параметры	${ displaystyle nu geq 0}$, Расстояние между опорной точкой и центром распределения двумерный, ${ displaystyle sigma geq 0}$, распространять
Поддерживать	${ Displaystyle х в [0, infty)}$
PDF	${ displaystyle { frac {x} { sigma ^ {2}}} exp left ({ frac {- (x ^ {2} + nu ^ {2})} {2 sigma ^ {2 }}} right) I_ {0} left ({ frac {x nu} { sigma ^ {2}}} right)}$
CDF	${ displaystyle 1-Q_ {1} left ({ frac { nu} { sigma}}, { frac {x} { sigma}} right)}$ куда Q1 это Q-функция Маркума
Иметь в виду	${ Displaystyle sigma { sqrt { pi / 2}} , , L_ {1/2} (- nu ^ {2} / 2 sigma ^ {2})}$
Дисперсия	${ displaystyle 2 sigma ^ {2} + nu ^ {2} - { frac { pi sigma ^ {2}} {2}} L_ {1/2} ^ {2} left ({ frac {- nu ^ {2}} {2 sigma ^ {2}}} right)}$
Асимметрия	(сложно)
Бывший. эксцесс	(сложно)

В теория вероятности, то Раздача риса или же Райское распределение (или, реже, Распределение риса) это распределение вероятностей величины циркулярно-симметричной двумерная нормальная случайная величина, возможно, с ненулевым средним (нецентральным). Он был назван в честь Стивен О. Райс.

Характеристика

В функция плотности вероятности является

${ displaystyle f (x mid nu, sigma) = { frac {x} { sigma ^ {2}}} exp left ({ frac {- (x ^ {2} + nu ^ {2})} {2 sigma ^ {2}}} right) I_ {0} left ({ frac {x nu} { sigma ^ {2}}} right),}$

куда я₀(z) является модифицированным Функция Бесселя первого рода с нулевым порядком.

В контексте Rician увядание, дистрибутив также часто переписывается с использованием Параметр формы ${ Displaystyle К = { гидроразрыва { nu ^ {2}} {2 sigma ^ {2}}}}$, определяемый как отношение вкладов мощности от трассы прямой видимости к остальным многолучевым путям, и Масштабный параметр ${ Displaystyle Omega = nu ^ {2} +2 sigma ^ {2}}$, определяемая как общая мощность, полученная на всех путях.^[1]

В характеристическая функция распределения Райса задается как:^[2][3]

${ Displaystyle { begin {align} chi _ {X} (t mid nu, sigma) = exp left (- { frac { nu ^ {2}} {2 sigma ^ {2 }}} right) & left [ Psi _ {2} left (1; 1, { frac {1} {2}}; { frac { nu ^ {2}} {2 sigma ^ {2}}}, - { frac {1} {2}} sigma ^ {2} t ^ {2} right) right. [8pt] & left. {} + I { sqrt {2}} sigma t Psi _ {2} left ({ frac {3} {2}}; 1, { frac {3} {2}}; { frac { nu ^ {2} } {2 sigma ^ {2}}}, - { frac {1} {2}} sigma ^ {2} t ^ {2} right) right], end {align}}}$

куда ${ Displaystyle Psi _ {2} влево ( альфа; гамма, гамма '; х, у вправо)}$ один из Конфлюэнтные гипергеометрические функции Хорна с двумя переменными и сходящаяся для всех конечных значений ${ displaystyle x}$ и ${ displaystyle y}$. Выдается:^[4][5]

${ Displaystyle Psi _ {2} left ( alpha; gamma, gamma '; x, y right) = sum _ {n = 0} ^ { infty} sum _ {m = 0} ^ { infty} { frac {( alpha) _ {m + n}} {( gamma) _ {m} ( gamma ') _ {n}}} { frac {x ^ {m} y ^ {n}} {m! n!}},}$

куда

${ displaystyle (x) _ {n} = x (x + 1) cdots (x + n-1) = { frac { Gamma (x + n)} { Gamma (x)}}}$

это возрастающий факториал.

Характеристики

Моменты

Первые несколько сырые моменты находятся:

${ displaystyle mu _ {1} ^ {'} = sigma { sqrt { pi / 2}} , , L_ {1/2} (- nu ^ {2} / 2 sigma ^ { 2})}$

${ displaystyle mu _ {2} ^ {'} = 2 sigma ^ {2} + nu ^ {2} ,}$

${ displaystyle mu _ {3} ^ {'} = 3 sigma ^ {3} { sqrt { pi / 2}} , , L_ {3/2} (- nu ^ {2} / 2 sigma ^ {2})}$

${ displaystyle mu _ {4} ^ {'} = 8 sigma ^ {4} +8 sigma ^ {2} nu ^ {2} + nu ^ {4} ,}$

${ displaystyle mu _ {5} ^ {'} = 15 sigma ^ {5} { sqrt { pi / 2}} , , L_ {5/2} (- nu ^ {2} / 2 sigma ^ {2})}$

${ displaystyle mu _ {6} ^ {'} = 48 sigma ^ {6} +72 sigma ^ {4} nu ^ {2} +18 sigma ^ {2} nu ^ {4} + nu ^ {6} ,}$

и, в общем, сырые моменты даются

${ Displaystyle му _ {к} ^ {'} = sigma ^ {k} 2 ^ {k / 2} , Gamma (1 ! + ! k / 2) , L_ {k / 2} (- nu ^ {2} / 2 sigma ^ {2}). ,}$

Здесь L_q(Икс) обозначает Полином Лагерра:

${ displaystyle L_ {q} (x) = L_ {q} ^ {(0)} (x) = M (-q, 1, x) = , _ {1} F_ {1} (- q; 1 ;Икс)}$

куда ${ Displaystyle М (а, б, г) = _ {1} F_ {1} (а; б; г)}$ это конфлюэнтная гипергеометрическая функция первого вида. Когда k четно, необработанные моменты становятся простыми полиномами от σ и ν, как в примерах выше.

По делу q = 1/2:

${ displaystyle { begin {align} L_ {1/2} (x) & = , _ {1} F_ {1} left (- { frac {1} {2}}; 1; x right ) & = e ^ {x / 2} left [ left (1-x right) I_ {0} left (- { frac {x} {2}} right) -xI_ {1} left (- { frac {x} {2}} right) right]. end {выравнивается}}}$

Второй центральный момент, то отклонение, является

${ displaystyle mu _ {2} = 2 sigma ^ {2} + nu ^ {2} - ( pi sigma ^ {2} / 2) , L_ {1/2} ^ {2} ( - nu ^ {2} / 2 sigma ^ {2}).}$

Обратите внимание, что ${ Displaystyle L_ {1/2} ^ {2} ( cdot)}$ обозначает квадрат полинома Лагерра ${ Displaystyle L_ {1/2} ( cdot)}$, а не обобщенный многочлен Лагерра ${ Displaystyle L_ {1/2} ^ {(2)} ( cdot).}$

Связанные дистрибутивы

• ${ Displaystyle R sim mathrm {Rice} left (| nu |, sigma right)}$ если ${ displaystyle R = { sqrt {X ^ {2} + Y ^ {2}}}}$ куда ${ Displaystyle Икс сим N влево ( ню соз тета, сигма ^ {2} вправо)}$ и ${ displaystyle Y sim N left ( nu sin theta, sigma ^ {2} right)}$ являются статистически независимыми нормальными случайными величинами и ${ displaystyle theta}$ - любое действительное число.
• Другой случай, когда ${ Displaystyle R sim mathrm {Рис} left ( nu, sigma right)}$ происходит из следующих шагов:

1. Создать ${ displaystyle P}$ иметь распределение Пуассона с параметром (также означает, для Пуассона) ${ displaystyle lambda = { frac { nu ^ {2}} {2 sigma ^ {2}}}.}$

2. Создать ${ displaystyle X}$ иметь распределение хи-квадрат с 2п + 2 степени свободы.

3. Установить ${ displaystyle R = sigma { sqrt {X}}.}$

• Если ${ Displaystyle R sim Operatorname {Rice} ( nu, 1)}$ тогда ${ displaystyle R ^ {2}}$ имеет нецентральное распределение хи-квадрат с двумя степенями свободы и параметром нецентральности ${ displaystyle nu ^ {2}}$.
• Если ${ Displaystyle R sim Operatorname {Rice} ( nu, 1)}$ тогда ${ displaystyle R}$ имеет нецентральное распределение ци с двумя степенями свободы и параметром нецентральности ${ displaystyle nu}$.
• Если ${ displaystyle R sim operatorname {Rice} (0, sigma)}$ тогда ${ displaystyle R sim operatorname {Rayleigh} ( sigma)}$, т.е. для частного случая распределения Райса, задаваемого формулой ${ displaystyle nu = 0}$, распределение принимает вид Распределение Рэлея, для которого дисперсия ${ displaystyle mu _ {2} = { frac {4- pi} {2}} sigma ^ {2}}$.
• Если ${ displaystyle R sim operatorname {Rice} (0, sigma)}$ тогда ${ displaystyle R ^ {2}}$ имеет экспоненциальное распределение.^[6]
• Если ${ displaystyle R sim Operatorname {Rice} left ( nu, sigma right)}$ тогда ${ displaystyle 1 / R}$ имеет обратное райсовское распределение.^[7]

• В сложенное нормальное распределение является одномерным частным случаем распределения Райса.

Предельные случаи

При больших значениях аргумента полином Лагерра принимает вид^[8]

${ displaystyle lim _ {x rightarrow - infty} L _ { nu} (x) = { frac {| x | ^ { nu}} { Gamma (1+ nu)}}.}$

Видно, что как ν становится большим или σ становится малым, среднее значение становится ν и дисперсия становится σ².

Переход к гауссовскому приближению происходит следующим образом. Из теории функций Бесселя имеем

${ displaystyle I _ { alpha} (z) rightarrow { frac {e ^ {z}} { sqrt {2 pi z}}} left (1 - { frac {4 alpha ^ {2}) -1} {8z}} + cdots right) { text {as}} z rightarrow infty}$

Итак, в целом ${ Displaystyle х ню / сигма ^ {2}}$ область, асимптотическое разложение рисовского распределения:

${ displaystyle { begin {align} f (x, nu, sigma) = {} & { frac {x} { sigma ^ {2}}} exp left ({ frac {- (x ^ {2} + nu ^ {2})} {2 sigma ^ {2}}} right) I_ {0} left ({ frac {x nu} { sigma ^ {2}}} right) { text {is}} & { frac {x} { sigma ^ {2}}} exp left ({ frac {- (x ^ {2} + nu ^ {2})} {2 sigma ^ {2}}} right) { sqrt { frac { sigma ^ {2}} {2 pi x nu}}} exp left ({ frac {2x nu} {2 sigma ^ {2}}} right) left (1 + { frac { sigma ^ {2}} {8x nu}} + cdots right) rightarrow {} & { frac {1} { sigma { sqrt {2 pi}}}} exp left (- { frac {(x- nu) ^ {2}} {2 sigma ^ { 2}}} right) { sqrt { frac {x} { nu}}}, ; ; ; { text {as}} { frac {x nu} { sigma ^ {2 }}} rightarrow infty end {выровнено}}}$

Более того, когда плотность сосредоточена вокруг ${ textstyle nu}$ и ${ textstyle | х- ню | ll sigma}$ из-за показателя Гаусса мы также можем написать ${ displaystyle { sqrt { frac {x} { nu}}} приблизительно 1}$ и, наконец, получить нормальное приближение

${ displaystyle f (x, nu, sigma) приблизительно { frac {1} { sigma { sqrt {2 pi}}}} exp left (- { frac {(x- nu ) ^ {2}} {2 sigma ^ {2}}} right), ; ; ; { frac { nu} { sigma}} gg 1}$

Приближение становится пригодным для ${ displaystyle { frac { nu} { sigma}}> 3}$

Оценка параметров (метод инверсии Коая)

Существует три различных метода оценки параметров распределения Райса (1) метод моментов,^{[9][10][11][12]} (2) метод максимального правдоподобия,^{[9][10][11][13]} и (3) метод наименьших квадратов.^{[нужна цитата ]} В первых двух методах интерес заключается в оценке параметров распределения ν и σ на основе выборки данных. Это можно сделать, используя метод моментов, например, выборочное среднее и стандартное отклонение выборки. Среднее значение выборки является оценкой μ₁^' а стандартное отклонение выборки является оценкой μ₂^1/2.

Ниже приводится эффективный метод, известный как «техника инверсии Коая».^[14] для решения оценочные уравнения на основе выборочного среднего и выборочного стандартного отклонения одновременно. Этот метод инверсии также известен как фиксированная точка формула SNR. Более ранние работы^[9][15] по методу моментов обычно используют метод поиска корней для решения проблемы, который неэффективен.

Во-первых, отношение выборочного среднего к стандартному отклонению выборки определяется как р, т.е. ${ Displaystyle г = му _ {1} ^ {'} / му _ {2} ^ {1/2}}$. Формула фиксированной точки для отношения сигнал / шум выражается как

${ displaystyle g ( theta) = { sqrt { xi {( theta)} left [1 + r ^ {2} right] -2}},}$

куда ${ displaystyle theta}$ - отношение параметров, т.е. ${ displaystyle theta = { frac { nu} { sigma}}}$, и ${ Displaystyle кси { влево ( тета справа)}}$ дан кем-то:

${ displaystyle xi { left ( theta right)} = 2+ theta ^ {2} - { frac { pi} {8}} exp {(- theta ^ {2} / 2) } left [(2+ theta ^ {2}) I_ {0} ( theta ^ {2} / 4) + theta ^ {2} I_ {1} ( theta ^ {2} / 4) вправо] ^ {2},}$

куда ${ displaystyle I_ {0}}$ и ${ displaystyle I_ {1}}$ находятся модифицированные функции Бесселя первого рода.

Обратите внимание, что ${ Displaystyle кси { влево ( тета справа)}}$ коэффициент масштабирования ${ displaystyle sigma}$ и связан с ${ displaystyle mu _ {2}}$ к:

${ displaystyle mu _ {2} = xi { left ( theta right)} sigma ^ {2}. ,}$

Чтобы найти фиксированную точку, ${ displaystyle theta ^ {*}}$, из ${ displaystyle g}$, выбирается начальное решение, ${ displaystyle { theta} _ {0}}$, что больше нижней границы, равной ${ Displaystyle { theta} _ { mathrm {нижний предел}} = 0}$ и происходит, когда ${ Displaystyle г = { sqrt { pi / (4- pi)}}}$^[14] (Обратите внимание, что это ${ Displaystyle г = му _ {1} ^ {'} / му _ {2} ^ {1/2}}$ распределения Рэлея). Это обеспечивает отправную точку для итерации, в которой используется функциональная композиция,^{[требуется разъяснение ]} и это продолжается до тех пор, пока ${ displaystyle left | g ^ {i} left ( theta _ {0} right) - theta _ {i-1} right |}$ меньше некоторого небольшого положительного значения. Здесь, ${ displaystyle g ^ {i}}$ обозначает композицию той же функции, ${ displaystyle g}$, ${ displaystyle i}$ раз. На практике мы связываем финальную ${ displaystyle theta _ {n}}$ для некоторого целого числа ${ displaystyle n}$ как неподвижная точка, ${ displaystyle theta ^ {*}}$, т.е. ${ Displaystyle тета ^ {*} = г влево ( тета ^ {*} вправо)}$.

Как только фиксированная точка найдена, оценки ${ displaystyle nu}$ и ${ displaystyle sigma}$ находятся с помощью функции масштабирования, ${ Displaystyle кси { влево ( тета справа)}}$, следующее:

${ displaystyle sigma = { frac { mu _ {2} ^ {1/2}} { sqrt { xi left ( theta ^ {*} right)}}},}$

и

${ Displaystyle Nu = { sqrt { left ( mu _ {1} ^ {'~ 2} + left ( xi left ( theta ^ {*} right) -2 right) sigma ^ {2} right)}}.}$

Чтобы еще больше ускорить итерацию, можно использовать метод поиска корней Ньютона.^[14] Этот конкретный подход очень эффективен.

Приложения

• В Евклидова норма из двумерный циркулярно-симметричный нормально распределенный случайный вектор.
• Rician увядание (за многолучевые помехи ))
• Влияние ошибки прицеливания на стрельбу по цели.^[16]

Смотрите также

Многомерная модель Rician используется при анализе разнесенных приемников в радиосвязи.^[17][18].

• Распределение Рэлея
• Стивен О. Райс (1907–1986)

Примечания

Рекомендации

• Абрамовиц М. и Стегун И. А. (ред.), Справочник по математическим функциям, Национальное бюро стандартов, 1964 г .; переизданный Dover Publications, 1965. ISBN  0-486-61272-4
• Райс, С.О., Математический анализ случайного шума. Технический журнал Bell System 24 (1945) 46–156.
• И. Солтани Бозчалой и Мин Лян (20 ноября 2007 г.). «Подход на основе индекса плавности к выбору вейвлет-параметров при устранении шумов и обнаружении неисправностей». Журнал звука и вибрации. 308 (1–2): 253–254. Bibcode:2007JSV ... 308..246B. Дои:10.1016 / j.jsv.2007.07.038.CS1 maint: использует параметр авторов (связь)
• Ван, Донг; Чжоу, Цян; Цуй, Квок-Люн (2017). «О распределении модуля вейвлет-коэффициентов Габора и верхней границе безразмерного индекса гладкости в случае аддитивных гауссовских шумов: еще раз». Журнал звука и вибрации. 395: 393–400. Дои:10.1016 / j.jsv.2017.02.013.
• Лю X. и Hanzo L., Единый точный анализ производительности BER асинхронных систем DS-CDMA с использованием модуляции BPSK по каналам с замиранием, IEEE Transactions on Wireless Communications, Volume 6, Issue 10, October 2007, pp. 3504–3509.
• Аннамалай А., Телламбура К. и Бхаргава В. К., Характеристики разнесенного приемника с равным усилением в беспроводных каналах, IEEE Transactions on Communications, Volume 48, October 2000, pp. 1732–1745.
• Эрдели, А., Магнус, В., Оберхеттингер, Ф. и Трикоми, Ф. Г., Высшие трансцендентные функции, том 1. McGraw-Hill Book Company Inc., 1953 год.
• Шривастава Х. М., Карлссон П. В. Кратные гауссовские гипергеометрические ряды. Эллис Хорвуд Лтд., 1985 г.
• Сиджберс Дж., Ден Деккер А. Дж., Шеундерс П. и Ван Дайк Д., «Оценка максимального правдоподобия параметров Райсовского распределения», IEEE Transactions on Medical Imaging, Vol. 17, № 3. С. 357–361, (1998).
• Варадараджан Д. и Халдар Дж. П., "Основа" мажоризация-минимизация "для изображений MR Rician и Non-Central Chi", IEEE Transactions on Medical Imaging, Vol. 34, нет. 10. С. 2191–2202, (2015)
• den Dekker, A.J., и Sijbers, J (декабрь 2014 г.). «Распределение данных на магнитно-резонансных изображениях: обзор». Physica Medica. 30 (7): 725–741. Дои:10.1016 / j.ejmp.2014.05.002. PMID  25059432.CS1 maint: использует параметр авторов (связь)
• Коай, К.Г. и Basser, P.J., Аналитически точная схема коррекции для выделения сигнала из МР-сигналов с шумом, Журнал магнитного резонанса, том 179, выпуск 2, стр. 317–322, (2006)
• Абди, А., Тепеделенлиоглу, К., Каве, М., и Гианнакис, Г. Об оценке параметра K для распределения замираний Райса, IEEE Communications Letters, Volume 5, Number 3, March 2001, pp. 92–94.
• Талукдар, К.К., и Лоуинг, Уильям Д. (март 1991 г.). «Оценка параметров распределения Райса». Журнал Акустического общества Америки. 89 (3): 1193–1197. Bibcode:1991ASAJ ... 89.1193T. Дои:10.1121/1.400532.CS1 maint: использует параметр авторов (связь)
• Бонни, Дж. М., Рену, Дж. П., и Занка, М. (ноябрь 1996 г.). «Оптимальное измерение величины и фазы по данным MR». Журнал магнитного резонанса, серия B. 113 (2): 136–144. Bibcode:1996JMRB..113..136B. Дои:10.1006 / jmrb.1996.0166. PMID  8954899.CS1 maint: использует параметр авторов (связь)

внешняя ссылка

• Код MATLAB для распределения Rice / Rician (PDF, среднее и дисперсия, а также создание случайных выборок)