Распределение Парето - Pareto distribution

Ограниченный Парето
Параметры	расположение (настоящий ); расположение (настоящий ); форма (реальный)
Поддержка
PDF
CDF
Значить	;
Медиана
Дисперсия	(это второй необработанный момент, а не дисперсия)
Асимметрия	(это k-й необработанный момент, а не перекос)

Тип Парето I
	Функция плотности вероятности; Функции плотности вероятности Парето типа I для различных с участием Так как подходы к распределению где это Дельта-функция Дирака.
	Кумулятивная функция распределения; Кумулятивные функции распределения Парето типа I для различных с участием
Параметры	масштаб (настоящий ); форма (реальный)
Поддержка
PDF
CDF
Значить
Медиана
Режим
Дисперсия
Асимметрия
Ex. эксцесс
Энтропия
MGF
CF
Информация Fisher	Правильно:

В Распределение Парето, названный в честь итальянского инженер-строитель, экономист, и социолог Вильфредо Парето,^[1] (Итальянский:[п а ˈ р е ː т о ] НАС: /пəˈрeɪтoʊ/ pə-РЭЙ-то ),^[2] это сила закона распределение вероятностей что используется в описании Социальное, контроль качества, научный, геофизический, актуарный, и многие другие типы наблюдаемых явлений. Первоначально применялся для описания распределение богатства в обществе, что соответствует тенденции, согласно которой большая часть богатства принадлежит небольшой части населения.^[3] В Принцип Парето или «правило 80-20», утверждающее, что 80% результатов обусловлены 20% причин, было названо в честь Парето, но концепции различны, и только распределения Парето со значением формы ( $α$ ) журнала₄5 ≈ 1,16 точно это отражают. Эмпирические наблюдения показали, что это распределение 80-20 подходит для широкого круга случаев, включая природные явления.^[4] и человеческая деятельность.^[5]

Определения

Если Икс это случайная переменная с распределением Парето (тип I),^[6] тогда вероятность того, что Икс больше некоторого числа Икс, т.е. функция выживания (также называемая хвостовой функцией), определяется как

{ displaystyle { overline {F}} (x) = Pr (X> x) = { begin {cases} left ({ frac {x _ { mathrm {m}}} {x}} right ) ^ { alpha} & x geq x _ { mathrm {m}}, 1 & x

где Икс_м является (обязательно положительным) минимально возможным значением Икс, и α - положительный параметр. Распределение Парето типа I характеризуется параметр масштаба Икс_м и параметр формы α, который известен как хвостовой индекс. Когда это распределение используется для моделирования распределения богатства, тогда параметр α называется Индекс Парето.

Кумулятивная функция распределения

Из определения кумулятивная функция распределения случайной величины Парето с параметрами α и Икс_м является

{ Displaystyle F_ {X} (х) = { begin {case} 1- left ({ frac {x _ { mathrm {m}}} {x}} right) ^ { alpha} & x geq x _ { mathrm {m}}, 0 & x

Функция плотности вероятности

Отсюда следует (по дифференциация ) что функция плотности вероятности является

{ displaystyle f_ {X} (x) = { begin {cases} { frac { alpha x _ { mathrm {m}} ^ { alpha}} {x ^ { alpha +1}}} & x geq x _ { mathrm {m}}, 0 & x

При нанесении на линейные оси распределение принимает знакомую J-образную кривую, которая приближается к каждой из ортогональных осей. асимптотически. Все сегменты кривой самоподобны (с учетом соответствующих масштабных коэффициентов). При построении в логарифмический график, распределение изображается прямой линией.

Свойства

Моменты и характерная функция

В ожидаемое значение из случайная переменная после распределения Парето

{ displaystyle operatorname {E} (X) = { begin {case} infty & alpha leq 1, { frac { alpha x _ { mathrm {m}}} { alpha -1} } & alpha> 1. end {case}}}

В отклонение из случайная переменная после распределения Парето

{ displaystyle operatorname {Var} (X) = { begin {cases} infty & alpha in (1,2], left ({ frac {x _ { mathrm {m}}} { alpha -1}} right) ^ {2} { frac { alpha} { alpha -2}} & alpha> 2. end {ases}}}

(Если α ≤ 1, дисперсия не существует.)

Сырье моменты находятся

{ displaystyle mu _ {n} '= { begin {case} infty & alpha leq n, { frac { alpha x _ { mathrm {m}} ^ {n}} { alpha -n}} & alpha> n. end {case}}}

В функция, производящая момент определяется только для неположительных значений т ≤ 0 как

{ displaystyle M left (t; alpha, x _ { mathrm {m}} right) = operatorname {E} left [e ^ {tX} right] = alpha (-x _ { mathrm { m}} t) ^ { alpha} Gamma (- alpha, -x _ { mathrm {m}} t)}

{ displaystyle M left (0, alpha, x _ { mathrm {m}} right) = 1.}

В характеристическая функция дан кем-то

{ displaystyle varphi (t; alpha, x _ { mathrm {m}}) = alpha (-ix _ { mathrm {m}} t) ^ { alpha} Gamma (- alpha, -ix_ { mathrm {m}} t),}

где Γ (а, Икс) это неполная гамма-функция.

Параметры могут быть решены с помощью метод моментов^{[необходимо разрешение неоднозначности ]}.^[7]

Условные распределения

В условное распределение вероятностей случайной величины, распределенной по Парето, при условии, что она больше или равна определенному числу ${ displaystyle x_ {1}}$ превышающий ${ displaystyle x _ { text {m}}}$ , является распределением Парето с тем же индексом Парето ${ displaystyle alpha}$ но с минимумом ${ displaystyle x_ {1}}$ вместо того ${ displaystyle x _ { text {m}}}$ .

Характеризационная теорема

Предположим ${ Displaystyle X_ {1}, X_ {2}, X_ {3}, dotsc}$ находятся независимые одинаково распределенные случайные переменные распределение вероятностей которого поддерживается на интервале ${ Displaystyle [х _ { текст {м}}, infty)}$ для некоторых ${ displaystyle x _ { text {m}}> 0}$ . Предположим, что для всех ${ displaystyle n}$ , две случайные величины ${ Displaystyle мин {X_ {1}, dotsc, X_ {п} }}$ и ${ displaystyle (X_ {1} + dotsb + X_ {n}) / min {X_ {1}, dotsc, X_ {n} }}$ независимы. Тогда обычное распределение - это распределение Парето.^{[нужна цитата ]}

Среднее геометрическое

В среднее геометрическое (г) является^[8]

{ displaystyle G = x _ { text {m}} exp left ({ frac {1} { alpha}} right).}

Гармоническое среднее

В гармоническое среднее (ЧАС) является^[8]

{ displaystyle H = x _ { text {m}} left (1 + { frac {1} { alpha}} right).}

Графическое представление

Характерный изогнутый 'длинный хвост 'распределение в линейном масштабе маскирует лежащую в основе простоту функции при нанесении на лог-лог-график, которая затем принимает форму прямой с отрицательным градиентом: Из формулы для функции плотности вероятности следует, что для Икс ≥ Икс_м,

{ displaystyle log f_ {X} (x) = log left ( alpha { frac {x _ { mathrm {m}} ^ { alpha}} {x ^ { alpha +1}}} справа) = log ( alpha x _ { mathrm {m}} ^ { alpha}) - ( alpha +1) log x.}

поскольку α положительна, градиент - (α + 1) отрицательно.

Связанные дистрибутивы

Обобщенные распределения Парето

Есть иерархия ^[6]^[9] распределений Парето, известных как распределения Парето типа I, II, III, IV и распределения Феллера – Парето.^[6]^[9]^[10] Тип Парето IV содержит Тип Парето I – III как частный случай. Феллер – Парето^[9]^[11] Распределение обобщает тип Парето IV.

Типы Парето I – IV

Иерархия распределения Парето представлена в следующей таблице, в которой сравниваются функции выживания (дополнительный CDF).

Когда μ = 0, тип распределения Парето II также известен как Распределение Lomax.^[12]

В этом разделе символ Икс_м, использованный ранее для обозначения минимального значения Икс, заменяется наσ.

Распределения Парето
	${ Displaystyle { overline {F}} (х) = 1-F (х)}$	Поддержка	Параметры
Тип I	${ displaystyle left [{ frac {x} { sigma}} right] ^ {- alpha}}$	${ Displaystyle х geq sigma}$	${ Displaystyle sigma> 0, альфа}$
Тип II	${ displaystyle left [1 + { frac {x- mu} { sigma}} right] ^ {- alpha}}$	${ Displaystyle х geq mu}$	${ displaystyle mu in mathbb {R}, sigma> 0, alpha}$
Lomax	${ displaystyle left [1 + { frac {x} { sigma}} right] ^ {- alpha}}$	${ Displaystyle х geq 0}$	${ Displaystyle sigma> 0, альфа}$
Тип III	${ displaystyle left [1+ left ({ frac {x- mu} { sigma}} right) ^ {1 / gamma} right] ^ {- 1}}$	${ Displaystyle х geq mu}$	${ displaystyle mu in mathbb {R}, sigma, gamma> 0}$
Тип IV	${ displaystyle left [1+ left ({ frac {x- mu} { sigma}} right) ^ {1 / gamma} right] ^ {- alpha}}$	${ Displaystyle х geq mu}$	${ displaystyle mu in mathbb {R}, sigma, gamma> 0, alpha}$

Параметр формы α это хвостовой индекс, μ это место, σ это масштаб, γ является параметром неравенства. Некоторые частные случаи типа Парето (IV):

{ Displaystyle Р (IV) ( сигма, сигма, 1, альфа) = Р (I) ( сигма, альфа),}

{ Displaystyle Р (IV) ( му, сигма, 1, альфа) = Р (II) ( му, сигма, альфа),}

{ Displaystyle P (IV) ( mu, sigma, gamma, 1) = P (III) ( mu, sigma, gamma).}

Конечность среднего, а также существование и конечность дисперсии зависят от хвостового индекса α (индекс неравенства γ). В частности, дробное δ- моменты конечны для некоторых δ > 0, как показано в таблице ниже, где δ не обязательно целое число.

Моменты распределений Парето I – IV (случай μ = 0)
	${ displaystyle operatorname {E} [X]}$	Состояние	${ displaystyle operatorname {E} [X ^ { delta}]}$	Состояние
Тип I	${ displaystyle { frac { sigma alpha} { alpha -1}}}$	${ displaystyle alpha> 1}$	${ displaystyle { frac { sigma ^ { delta} alpha} { alpha - delta}}}$	${ Displaystyle дельта < альфа}$
Тип II	${ displaystyle { frac { sigma} { alpha -1}} + mu}$	${ displaystyle alpha> 1}$	${ displaystyle { frac { sigma ^ { delta} Gamma ( alpha - delta) Gamma (1+ delta)} { Gamma ( alpha)}}}$	${ Displaystyle 0 < дельта < альфа}$
Тип III	${ Displaystyle сигма Гамма (1- гамма) Гамма (1+ гамма)}$	${ Displaystyle -1 < гамма <1}$	${ displaystyle sigma ^ { delta} Gamma (1- gamma delta) Gamma (1+ gamma delta)}$	${ displaystyle - gamma ^ {- 1} < delta < gamma ^ {- 1}}$
Тип IV	${ Displaystyle { гидроразрыва { сигма Гамма ( альфа - гамма) Гамма (1+ гамма)} { Гамма ( альфа)}}}$	${ Displaystyle -1 < гамма < альфа}$	${ displaystyle { frac { sigma ^ { delta} Gamma ( alpha - gamma delta) Gamma (1+ gamma delta)} { Gamma ( alpha)}}}$	${ displaystyle - gamma ^ {- 1} < delta < alpha / gamma}$

Распределение Феллера – Парето

Вальщик^[9]^[11] определяет переменную Парето преобразованием U = Y⁻¹ - 1 из бета случайная величина Y, функция плотности вероятности которого

{ displaystyle f (y) = { frac {y ^ { gamma _ {1} -1} (1-y) ^ { gamma _ {2} -1}} {B ( gamma _ {1} , gamma _ {2})}}, qquad 0 0,}

где B( ) это бета-функция. Если

{ Displaystyle W = mu + sigma (Y ^ {- 1} -1) ^ { gamma}, qquad sigma> 0, gamma> 0,}

тогда W имеет распределение Феллера – Парето FP (μ, σ, γ, γ₁, γ₂).^[6]

Если ${ Displaystyle U_ {1} sim Gamma ( delta _ {1}, 1)}$ и ${ Displaystyle U_ {2} sim Gamma ( delta _ {2}, 1)}$ независимы Гамма-переменные, другая конструкция переменной Феллера – Парето (FP) - это^[13]

{ displaystyle W = mu + sigma left ({ frac {U_ {1}} {U_ {2}}} right) ^ { gamma}}

и мы пишем W ~ FP (μ, σ, γ, δ₁, δ₂). Частные случаи распределения Феллера – Парето:

{ Displaystyle FP ( sigma, sigma, 1,1, альфа) = P (I) ( sigma, alpha)}

{ Displaystyle FP ( му, сигма, 1,1, альфа) = п (II) ( му, сигма, альфа)}

{ Displaystyle FP ( му, сигма, гамма, 1,1) = п (III) ( му, сигма, гамма)}

{ displaystyle FP ( mu, sigma, gamma, 1, alpha) = P (IV) ( mu, sigma, gamma, alpha).}

Связь с экспоненциальным распределением

Распределение Парето связано с экспоненциальное распределение следующим образом. Если Икс распределяется по Парето с минимальным Икс_м и индексα, тогда

{ displaystyle Y = log left ({ frac {X} {x _ { mathrm {m}}}} right)}

является экспоненциально распределенный с параметром скоростиα. Эквивалентно, если Y экспоненциально распределяется со скоростьюα, тогда

{ Displaystyle х _ { mathrm {m}} е ^ {Y}}

распределяется по Парето с минимальным Икс_м и индексα.

Это можно показать, используя стандартные методы замены переменных:

{ Displaystyle { begin {align} Pr (Y

Последнее выражение представляет собой кумулятивную функцию распределения экспоненциального распределения со скоростьюα.

Распределение Парето можно построить с помощью иерархических экспоненциальных распределений.^[14]. Позволять

${ displaystyle phi | a sim { text {Exp}} (a), quad eta | phi sim { text {Exp}} ( phi)}$ . Тогда у нас есть ${ displaystyle p ( eta | a) = { frac {a} {(a + eta) ^ {2}}}}$ .

Отношение к логнормальному распределению

Распределение Парето и логнормальное распределение альтернативные распределения для описания тех же типов величин. Одна из связей между ними заключается в том, что они оба являются распределениями экспоненты случайных величин, распределенных в соответствии с другими общими распределениями, соответственно экспоненциальное распределение и нормальное распределение. (Увидеть предыдущий раздел.)

Связь с обобщенным распределением Парето

Распределение Парето - частный случай обобщенное распределение Парето, который является семейством распределений аналогичной формы, но содержит дополнительный параметр таким образом, что носитель распределения либо ограничен снизу (в переменной точке), либо ограничен как сверху, так и снизу (где оба являются переменными), с Распределение Lomax как частный случай. В это семейство входят также несмещенные и сдвинутые экспоненциальные распределения.

Распределение Парето с масштабом ${ displaystyle x_ {m}}$ и форма ${ displaystyle alpha}$ эквивалентно обобщенному распределению Парето с положением ${ displaystyle mu = x_ {m}}$ , масштаб ${ displaystyle sigma = x_ {m} / alpha}$ и форма ${ Displaystyle xi = 1 / альфа}$ . И наоборот, можно получить распределение Парето из GPD следующим образом: ${ displaystyle x_ {m} = sigma / xi}$ и ${ Displaystyle альфа = 1 / xi}$ .

Ограниченное распределение Парето

Ограниченное (или усеченное) распределение Парето имеет три параметра: α, L и ЧАС. Как в стандартном распределении Парето α определяет форму. L обозначает минимальное значение, а ЧАС обозначает максимальное значение.

В функция плотности вероятности является

{ displaystyle { frac { alpha L ^ { alpha} x ^ {- alpha -1}} {1- left ({ frac {L} {H}} right) ^ { alpha}} }}

,

где L ≤ Икс ≤ ЧАС, и α > 0.

Генерация ограниченных случайных величин Парето

Если U является равномерно распределены на (0, 1), затем применяя метод обратного преобразования ^[15]

{ displaystyle U = { frac {1-L ^ { alpha} x ^ {- alpha}} {1 - ({ frac {L} {H}}) ^ { alpha}}}}

{ displaystyle x = left (- { frac {UH ^ { alpha} -UL ^ { alpha} -H ^ { alpha}} {H ^ { alpha} L ^ { alpha}}}} справа) ^ {- { frac {1} { alpha}}}}

является ограниченным распределением по Парето.^{[нужна цитата ]}

Симметричное распределение Парето

Целью симметричного распределения Парето и нулевого симметричного распределения Парето является получение некоторого специального статистического распределения с острым пиком вероятности и симметричными длинными хвостами вероятности. Эти два распределения получены из распределения Парето. Длинный хвост вероятности обычно означает, что вероятность медленно убывает. Распределение Парето во многих случаях выполняет подобающую работу. Но если распределение имеет симметричную структуру с двумя медленно затухающими хвостами, Парето не смог бы этого сделать. Тогда вместо этого применяется симметричное распределение Парето или нулевое симметричное распределение Парето.^[16]

Кумулятивная функция распределения (CDF) симметричного распределения Парето определяется следующим образом:^[16]

${ Displaystyle F (X) = P (x$

Соответствующая функция плотности вероятности (PDF):^[16]

${ displaystyle p (x) = {ab ^ {a} over 2 (b + left vert x-b right vert) ^ {a + 1}}, X in R}$

Это распределение имеет два параметра: a и b. Он симметричен по b. Тогда математическое ожидание равно b. Когда он имеет следующие отклонения:

${ Displaystyle E ((xb) ^ {2}) = int _ {- infty} ^ { infty} (xb) ^ {2} p (x) dx = {2b ^ {2} over (a -2) (а-1)}}$

CDF нулевого симметричного распределения Парето (ZSP) определяется следующим образом:

${ Displaystyle F (X) = P (x$

Соответствующий PDF-файл:

${ displaystyle p (x) = {ab ^ {a} over 2 (b + left vert x right vert) ^ {a + 1}}, X in R}$

Это распределение симметрично нулю. Параметр связан со скоростью убывания вероятности и представляет собой пиковую величину вероятности.^[16]

Многомерное распределение Парето

Одномерное распределение Парето было расширено до многомерный Распределение Парето.^[17]

Статистические выводы

Оценка параметров

В функция правдоподобия для параметров распределения Парето α и Икс_м, учитывая независимую образец Икс = (Икс₁, Икс₂, ..., Икс_п), является

{ displaystyle L ( alpha, x _ { mathrm {m}}) = prod _ {i = 1} ^ {n} alpha { frac {x _ { mathrm {m}} ^ { alpha}} {x_ {i} ^ { alpha +1}}} = alpha ^ {n} x _ { mathrm {m}} ^ {n alpha} prod _ {i = 1} ^ {n} { frac {1} {x_ {i} ^ { alpha +1}}}.}

Следовательно, функция логарифмического правдоподобия имеет вид

{ displaystyle ell ( alpha, x _ { mathrm {m}}) = n ln alpha + n alpha ln x _ { mathrm {m}} - ( alpha +1) sum _ {i = 1} ^ {n} ln x_ {i}.}

Видно, что ${ Displaystyle ell ( альфа, х _ { mathrm {m}})}$ монотонно возрастает с увеличением Икс_м, то есть чем больше значение Икс_м, тем больше значение функции правдоподобия. Следовательно, поскольку Икс ≥ Икс_м, заключаем, что

{ displaystyle { widehat {x}} _ { mathrm {m}} = min _ {i} {x_ {i}}.}

Чтобы найти оценщик для α, вычисляем соответствующую частную производную и определяем, где она равна нулю:

{ displaystyle { frac { partial ell} { partial alpha}} = { frac {n} { alpha}} + n ln x _ { mathrm {m}} - sum _ {i = 1} ^ {n} ln x_ {i} = 0.}

Таким образом максимальная вероятность оценщик для α является:

{ displaystyle { widehat { alpha}} = { frac {n} { sum _ {i} ln (x_ {i} / { widehat {x}} _ { mathrm {m}})} }.}

Ожидаемая статистическая ошибка:^[18]

{ displaystyle sigma = { frac { widehat { alpha}} { sqrt {n}}}.}

Малик (1970)^[19] дает точное совместное распределение ${ displaystyle ({ hat {x}} _ { mathrm {m}}, { hat { alpha}})}$ . Особенно, ${ displaystyle { hat {x}} _ { mathrm {m}}}$ и ${ displaystyle { hat { alpha}}}$ находятся независимый и ${ displaystyle { hat {x}} _ { mathrm {m}}}$ Парето с масштабным параметром Икс_м и параметр формы nα, в то время как ${ displaystyle { hat { alpha}}}$ имеет обратное гамма-распределение с параметрами формы и масштаба п - 1 и nαсоответственно.

Возникновение и приложения

Общее

Вильфредо Парето изначально использовал этот дистрибутив для описания распределение богатства среди индивидов, поскольку это, казалось, довольно хорошо показывает, что большая часть богатства любого общества принадлежит меньшему проценту людей в этом обществе. Он также использовал его для описания распределения доходов.^[20] Эта идея иногда выражается проще как Принцип Парето или «правило 80-20», согласно которому 20% населения контролирует 80% богатства.^[21] Однако правило 80-20 соответствует определенному значению α, и фактически данные Парето о британских налогах на прибыль в его Cours d'économie politique указывает на то, что около 30% населения имели около 70% дохода.^{[нужна цитата ]} В функция плотности вероятности График (PDF) в начале этой статьи показывает, что «вероятность» или доля населения, владеющего небольшим количеством богатства на человека, довольно высока, а затем неуклонно уменьшается по мере увеличения богатства. (Однако распределение Парето нереально для богатства на нижнем уровне. чистая стоимость может даже быть отрицательным.) Это распределение не ограничивается описанием богатства или дохода, но ко многим ситуациям, в которых равновесие находится в распределении «малого» к «большому». Следующие примеры иногда рассматриваются как приблизительно распределенные по Парето:

Размеры населенных пунктов (несколько городов, много деревень / деревень)^[22]^[23]
Распределение размера файлов интернет-трафика, использующего протокол TCP (много файлов меньшего размера, несколько файлов большего размера)^[22]
Накопитель на жестком диске частота ошибок^[24]
Кластеры Конденсат Бозе – Эйнштейна около полный ноль^[25]

Подгонка кумулятивного распределения Парето (Ломакса) к максимальным однодневным осадкам с использованием CumFreq, смотрите также распределительная арматура

Ценности запасы нефти на нефтяных месторождениях (несколько большие поля, много небольшие поля )^[22]
Распределение длин в заданиях суперкомпьютеров (несколько крупных, много мелких)^[26]
Стандартизированная доходность по отдельным акциям ^[22]
Размеры песчинок ^[22]
Размер метеоритов
Степень тяжести большого несчастный случай убытки по определенным направлениям деятельности, таким как общая ответственность, коммерческие автомобили и компенсация работникам.^[27]^[28]
Количество времени, в течение которого пользователь Пар проведу играя в разные игры. (В некоторые игры играют много, но в большинство почти никогда не играют.) [2]
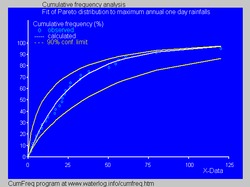
В гидрология Распределение Парето применяется к экстремальным явлениям, таким как ежегодные максимальные однодневные осадки и сток рек.^[29] На синем рисунке показан пример подгонки распределения Парето к ранжированным годовым максимальным однодневным осадкам, показывающий также 90% пояс уверенности на основе биномиальное распределение. Данные об осадках представлены построение позиций как часть совокупный частотный анализ.

Связь с законом Ципфа

Распределение Парето - это непрерывное распределение вероятностей. Закон Ципфа, также иногда называемый дзета-распределение, представляет собой дискретное распределение, разделяющее значения на простое ранжирование. Оба представляют собой простой степенной закон с отрицательной экспонентой, масштабированный так, чтобы их кумулятивные распределения равнялись 1. Коэффициенты Ципфа можно получить из распределения Парето, если ${ displaystyle x}$ ценности (доходы) разбиты на ${ displaystyle N}$ ранжирует так, чтобы количество людей в каждом бункере соответствовало шаблону 1 / ранг. Распределение нормализовано путем определения ${ displaystyle x_ {m}}$ так что ${ displaystyle alpha x _ { mathrm {m}} ^ { alpha} = { frac {1} {H (N, alpha -1)}}}$ где ${ Displaystyle Н (N, альфа -1)}$ это обобщенный номер гармоники. Это делает функцию плотности вероятности Ципфа выводимой из функции Парето.

{ displaystyle f (x) = { frac { alpha x _ { mathrm {m}} ^ { alpha}} {x ^ { alpha +1}}} = { frac {1} {x ^ { s} H (N, s)}}}

где ${ displaystyle s = alpha -1}$ и ${ displaystyle x}$ - целое число, представляющее ранг от 1 до N, где N - категория с наивысшим доходом. Таким образом, случайно выбранный человек (или слово, ссылка на веб-сайт или город) из населения (или языка, Интернета или страны) имеет ${ displaystyle f (x)}$ вероятность ранжирования ${ displaystyle x}$ .

Отношение к «принципу Парето»

"80-20 закон ", согласно которому 20% всех людей получают 80% всего дохода, а 20% самых богатых 20% получают 80% этих 80%, и так далее, верно, когда индекс Парето ${ displaystyle alpha = log _ {4} 5 = { cfrac { log _ {10} 5} { log _ {10} 4}} приблизительно 1,161}$ . Этот результат может быть получен из Кривая Лоренца формула, приведенная ниже. Кроме того, были показаны следующие^[30] быть математически эквивалентным:

Доход распределяется по распределению Парето с индексом α > 1.
Есть какое-то число 0 ≤п ≤ 1/2 такая, что 100п % всех людей получают 100 (1 -п)% от всего дохода, и аналогично для каждого реального (не обязательно целого) п > 0, 100п^п % всех людей получают 100 (1 -п)^п процент от всего дохода. α и п связаны

{ displaystyle 1 - { frac {1} { alpha}} = { frac { ln (1-p ^ {n})} { ln (1- (1-p) ^ {n})} }}

Это относится не только к доходу, но также и к богатству или ко всему, что можно смоделировать с помощью этого распределения.

Это исключает распределения Парето, в которых 0 <α ≤ 1, которые, как отмечалось выше, имеют бесконечное ожидаемое значение и поэтому не могут разумно моделировать распределение доходов.

Связь с законом Прайса

Закон квадратного корня цены иногда предлагается как собственность или аналогично распределению Парето. Однако закон действует только в том случае, если ${ Displaystyle альфа = 1}$ . Обратите внимание, что в этом случае общая и ожидаемая сумма богатства не определены, и правило применяется только асимптотически к случайным выборкам. Упомянутый выше расширенный принцип Парето является гораздо более общим правилом.

Кривая Лоренца и коэффициент Джини

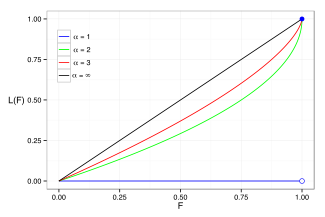
Кривые Лоренца для ряда распределений Парето. Дело α = ∞ соответствует идеально равному распределению (г = 0) и α = 1 строка соответствует полному неравенству (г = 1)

В Кривая Лоренца часто используется для характеристики распределения доходов и богатства. Для любого распределения кривая Лоренца L(F) записывается в формате PDF ж или CDF F так как

{ displaystyle L (F) = { frac { int _ {x _ { mathrm {m}}} ^ {x (F)} xf (x) , dx} { int _ {x _ { mathrm { m}}} ^ { infty} xf (x) , dx}} = { frac { int _ {0} ^ {F} x (F ') , dF'} { int _ {0} ^ {1} х (F ') , dF'}}}

где Икс(F) является обратным к CDF. Для распределения Парето

{ displaystyle x (F) = { frac {x _ { mathrm {m}}} {(1-F) ^ { frac {1} { alpha}}}}}

а кривая Лоренца рассчитывается как

{ Displaystyle L (F) = 1- (1-F) ^ {1 - { frac {1} { alpha}}},}

Для ${ Displaystyle 0 < альфа leq 1}$ знаменатель бесконечен, что дает L= 0. Примеры кривой Лоренца для ряда распределений Парето показаны на графике справа.

Согласно с Oxfam (2016) самые богатые 62 человека имеют такое же состояние, как и самая бедная половина населения мира.^[31] Мы можем оценить индекс Парето, который применим к этой ситуации. Полагая ε равным ${ displaystyle 62 / (7 times 10 ^ {9})}$ у нас есть:

{ Displaystyle L (1/2) = 1-L (1- varepsilon)}

или

{ displaystyle 1- (1/2) ^ {1 - { frac {1} { alpha}}} = varepsilon ^ {1 - { frac {1} { alpha}}}}

Решение в том, что α составляет около 1,15, и около 9% состояния принадлежит каждой из двух групп. Но на самом деле 69% беднейшего взрослого населения мира владеют лишь 3% богатства.^[32]

В Коэффициент Джини является мерой отклонения кривой Лоренца от линии равнораспределения, которая представляет собой линию, соединяющую [0, 0] и [1, 1], которая показана черным цветом (α = ∞) на графике Лоренца справа. В частности, коэффициент Джини в два раза больше площади между кривой Лоренца и линией равнораспределения. Затем рассчитывается коэффициент Джини для распределения Парето (для ${ displaystyle alpha geq 1}$ ) быть

{ displaystyle G = 1-2 left ( int _ {0} ^ {1} L (F) , dF right) = { frac {1} {2 alpha -1}}}

(см. Aaberge 2005).

Вычислительные методы

Генерация случайной выборки

Случайные выборки могут быть сгенерированы с помощью выборка с обратным преобразованием. Учитывая случайную вариацию U взяты из равномерное распределение на единичном интервале (0, 1] переменная Т данный

{ Displaystyle Т = { гидроразрыва {х _ { mathrm {m}}} {U ^ {1 / alpha}}}}

распределяется по Парето.^[33] Если U равномерно распределен на [0, 1), его можно заменить на (1 -U).

Смотрите также

использованная литература

^ Аморосо, Луиджи (1938). "ВИЛЬФРЕДО ПАРЕТО". Econometrica (до 1986 г.); Jan 1938; 6, 1; ProQuest. 6.
^ "Парето". Словарь Merriam-Webster. Получено 28 июля 2019.
^ Парето, Вильфредо (1898). "Cours d'economie politique". Журнал политической экономии. 6.
^ ВАН МОНТФОРТ, M.A.J. (1986). «Обобщенное распределение Парето применительно к глубине дождя». Журнал гидрологических наук. 31 (2): 151–162. Дои:10.1080/02626668609491037.
^ Оанча, Богдан (2017). «Неравенство доходов в Румынии: экспоненциально-Парето-распределение». Physica A: Статистическая механика и ее приложения. 469: 486–498. Bibcode:2017PhyA..469..486O. Дои:10.1016 / j.physa.2016.11.094.
^ ^а ^б ^c ^d Барри С. Арнольд (1983). Распределения Парето. Международное кооперативное издательство. ISBN 978-0-89974-012-6.
^ С. Хуссейн, С. Бхатти (2018). Оценка параметров распределения Парето: некоторые модифицированные оценки момента. Международный научно-технический журнал Maejo 12(1):11-27
^ ^а ^б Джонсон Н.Л., Коц С., Балакришнан Н. (1994) Непрерывные одномерные распределения Том 1. Ряды Уайли в вероятности и статистике.
^ ^а ^б ^c ^d Джонсон, Коц и Балакришнан (1994), (20.4).
^ Кристиан Клейбер и Самуэль Коц (2003). Статистические распределения размеров в экономике и актуарных науках. Wiley. ISBN 978-0-471-15064-0.
^ ^а ^б Феллер, В. (1971). Введение в теорию вероятностей и ее приложения. II (2-е изд.). Нью-Йорк: Вили. п. 50. "Плотности (4.3) иногда называют в честь экономиста Парето. Считалось (довольно наивно с современной статистической точки зрения), что распределение доходов должно иметь хвост с плотностью ~ Топор^−α так как Икс → ∞."
^ Ломакс, К. С. (1954). «Бизнес-сбои. Еще один пример анализа данных о сбоях». Журнал Американской статистической ассоциации. 49 (268): 847–52. Дои:10.1080/01621459.1954.10501239.
^ Чотикапанич, Дуангкамон (16 сентября 2008 г.). «Глава 7: Парето и обобщенные распределения Парето». Моделирование распределения доходов и кривых Лоренца. С. 121–22. ISBN 9780387727967.
^ Белый, Джентри (2006). Байесовское полупараметрическое пространственное и совместное пространственно-временное моделирование (Дипломная работа). Университет Миссури - Колумбия. раздел 5.3.1
^ http://www.cs.bgu.ac.il/~mps042/invtransnote.htm
^ ^а ^б ^c ^d Хуан, Сяо-дон (2004). «Мультимасштабная модель для видеотрафика MPEG-4 с различной скоростью передачи данных». IEEE Transactions on Broadcasting. 50 (3): 323–334. Дои:10.1109 / TBC.2004.834013.
^ Рутцен, Хольгер; Тайвиди, Надер (2006). «Многомерные обобщенные распределения Парето». Бернулли. 12 (5): 917–30. CiteSeerX 10.1.1.145.2991. Дои:10.3150 / bj / 1161614952.
^ М. Э. Дж. Ньюман (2005). «Степенные законы, распределения Парето и закон Ципфа». Современная физика. 46 (5): 323–51. arXiv:cond-mat / 0412004. Bibcode:2005ConPh..46..323N. Дои:10.1080/00107510500052444. S2CID 202719165.
^ Х. Дж. Малик (1970). «Оценка параметров распределения Парето». Метрика. 15: 126–132. Дои:10.1007 / BF02613565. S2CID 124007966.
^ Парето, Вильфредо, Cours d'Economie Politique: Nouvelle édition par G.-H. Bousquet et G. Busino, Librairie Droz, Женева, 1964, стр. 299–345.
^ Для двухквантильного населения, где примерно 18% населения владеет 82% богатства, Индекс Тейла принимает значение 1.
^ ^а ^б ^c ^d ^е Рид, Уильям Дж .; и другие. (2004). «Двойное логнормальное распределение Парето - новая параметрическая модель для распределений размеров». Коммуникации в статистике - теория и методы. 33 (8): 1733–53. CiteSeerX 10.1.1.70.4555. Дои:10.1081 / sta-120037438. S2CID 13906086.
^ Рид, Уильям Дж. (2002). «О ранговом распределении населенных пунктов». Журнал региональной науки. 42 (1): 1–17. Дои:10.1111/1467-9787.00247. S2CID 154285730.
^ Шредер, Бьянка; Дамур, Сотириос; Гилл, Филипа (24 февраля 2010 г.). «Понимание скрытых ошибок сектора и способы защиты от них» (PDF). 8-я конференция Usenix по файловым технологиям и технологиям хранения (FAST 2010). Получено 2010-09-10. Мы экспериментировали с 5 различными распределениями (геометрическим, Вейбулла, Рэлея, Парето и логнормальным), которые обычно используются в контексте надежности системы, и оценили их соответствие через общие квадраты разностей между фактической и предполагаемой частотами (χ² статистика). Мы последовательно обнаружили, что во всех моделях геометрическое распределение плохо согласуется, а распределение Парето дает наилучшее соответствие.
^ Юджи Иджири; Саймон, Герберт А. (май 1975 г.). «Некоторые распределения, связанные со статистикой Бозе – Эйнштейна». Proc. Natl. Акад. Sci. Соединенные Штаты Америки. 72 (5): 1654–57. Bibcode:1975PNAS ... 72.1654I. Дои:10.1073 / pnas.72.5.1654. ЧВК 432601. PMID 16578724.
^ Харчол-Балтер, Мор; Дауни, Аллен (август 1997 г.). «Использование распределений времени жизни процессов для динамической балансировки нагрузки» (PDF). ACM-транзакции в компьютерных системах. 15 (3): 253–258. Дои:10.1145/263326.263344. S2CID 52861447.
^ Клейбер и Коц (2003): стр. 94.
^ Сил, Х. (1980). «Вероятности выживания, основанные на распределении требований Парето». Бюллетень АСТИН. 11: 61–71. Дои:10.1017 / S0515036100006620.
^ CumFreq, программное обеспечение для кумулятивного частотного анализа и подбора распределения вероятностей [1]
^ Харди, Майкл (2010). «Закон Парето». Математический интеллигент. 32 (3): 38–43. Дои:10.1007 / s00283-010-9159-2. S2CID 121797873.
^ «62 человека владеют тем же, что и половина мира, - говорится в отчете Oxfam Davos». Oxfam. Янв 2016.
^ «Отчет о мировом благосостоянии за 2013 год». Credit Suisse. Октябрь 2013. с. 22. Архивировано из оригинал на 2015-02-14. Получено 2016-01-24.
^ Танидзаки, Хисаши (2004). Вычислительные методы в статистике и эконометрике. CRC Press. п. 133. ISBN 9780824750886.

Заметки

М. О. Лоренц (1905). «Методы измерения концентрации богатства». Публикации Американской статистической ассоциации. 9 (70): 209–19. Bibcode:1905PAmSA ... 9..209L. Дои:10.2307/2276207. JSTOR 2276207.
Парето, Вильфредо (1965). Librairie Droz (ред.). Ecrits sur la Courbe de la répartition de la richesse. Uvres complete: T. III. п. 48. ISBN 9782600040211.

Парето, Вильфредо (1895). "La legge della domanda". Giornale Degli Economisti. 10: 59–68.
Парето, Вильфредо (1896). "Cours d'économie politique". Дои:10.1177/000271629700900314. S2CID 143528002. Цитировать журнал требует | журнал = (Помогите)

внешние ссылки

«Распределение Парето», Энциклопедия математики, EMS Press, 2001 [1994]
Вайсштейн, Эрик В. «Распределение Парето». MathWorld.
Оберже, Рольф (май 2005 г.), Ядерная семья Джини (PDF)

Crovella, Марк Э.; Беставрос, Азер (декабрь 1997 г.). Самоподобие в интернет-трафике: доказательства и возможные причины (PDF). Транзакции IEEE / ACM в сети. 5. С. 835–846.

syntraf1.c это Программа C для генерации синтетического пакетного трафика с ограниченным размером пакета Парето и экспоненциальным временем между пакетами.

[1] Аморосо, Луиджи (1938). "ВИЛЬФРЕДО ПАРЕТО". Econometrica (до 1986 г.); Jan 1938; 6, 1; ProQuest. 6.

[2] "Парето". Словарь Merriam-Webster. Получено 28 июля 2019.

[3] Парето, Вильфредо (1898). "Cours d'economie politique". Журнал политической экономии. 6.

[4] ВАН МОНТФОРТ, M.A.J. (1986). «Обобщенное распределение Парето применительно к глубине дождя». Журнал гидрологических наук. 31 (2): 151–162. Дои:10.1080/02626668609491037.

[5] Оанча, Богдан (2017). «Неравенство доходов в Румынии: экспоненциально-Парето-распределение». Physica A: Статистическая механика и ее приложения. 469: 486–498. Bibcode:2017PhyA..469..486O. Дои:10.1016 / j.physa.2016.11.094.

[arnold-6] а ^б ^c ^d Барри С. Арнольд (1983). Распределения Парето. Международное кооперативное издательство. ISBN 978-0-89974-012-6.

[7] С. Хуссейн, С. Бхатти (2018). Оценка параметров распределения Парето: некоторые модифицированные оценки момента. Международный научно-технический журнал Maejo 12(1):11-27

[Johnson1994-8] а ^б Джонсон Н.Л., Коц С., Балакришнан Н. (1994) Непрерывные одномерные распределения Том 1. Ряды Уайли в вероятности и статистике.

[jkb94-9] а ^б ^c ^d Джонсон, Коц и Балакришнан (1994), (20.4).

[kk03-10] Кристиан Клейбер и Самуэль Коц (2003). Статистические распределения размеров в экономике и актуарных науках. Wiley. ISBN 978-0-471-15064-0.

[feller-11] а ^б Феллер, В. (1971). Введение в теорию вероятностей и ее приложения. II (2-е изд.). Нью-Йорк: Вили. п. 50. "Плотности (4.3) иногда называют в честь экономиста Парето. Считалось (довольно наивно с современной статистической точки зрения), что распределение доходов должно иметь хвост с плотностью ~ Топор^−α так как Икс → ∞."

[12] Ломакс, К. С. (1954). «Бизнес-сбои. Еще один пример анализа данных о сбоях». Журнал Американской статистической ассоциации. 49 (268): 847–52. Дои:10.1080/01621459.1954.10501239.

[13] Чотикапанич, Дуангкамон (16 сентября 2008 г.). «Глава 7: Парето и обобщенные распределения Парето». Моделирование распределения доходов и кривых Лоренца. С. 121–22. ISBN 9780387727967.

[14] Белый, Джентри (2006). Байесовское полупараметрическое пространственное и совместное пространственно-временное моделирование (Дипломная работа). Университет Миссури - Колумбия. раздел 5.3.1

[15] ttp://www.cs.bgu.ac.il/~mps042/invtransnote.htm

[:0-16] а ^б ^c ^d Хуан, Сяо-дон (2004). «Мультимасштабная модель для видеотрафика MPEG-4 с различной скоростью передачи данных». IEEE Transactions on Broadcasting. 50 (3): 323–334. Дои:10.1109 / TBC.2004.834013.

[17] Рутцен, Хольгер; Тайвиди, Надер (2006). «Многомерные обобщенные распределения Парето». Бернулли. 12 (5): 917–30. CiteSeerX 10.1.1.145.2991. Дои:10.3150 / bj / 1161614952.

[18] М. Э. Дж. Ньюман (2005). «Степенные законы, распределения Парето и закон Ципфа». Современная физика. 46 (5): 323–51. arXiv:cond-mat / 0412004. Bibcode:2005ConPh..46..323N. Дои:10.1080/00107510500052444. S2CID 202719165.

[19] Х. Дж. Малик (1970). «Оценка параметров распределения Парето». Метрика. 15: 126–132. Дои:10.1007 / BF02613565. S2CID 124007966.

[20] Парето, Вильфредо, Cours d'Economie Politique: Nouvelle édition par G.-H. Bousquet et G. Busino, Librairie Droz, Женева, 1964, стр. 299–345.

[21] Для двухквантильного населения, где примерно 18% населения владеет 82% богатства, Индекс Тейла принимает значение 1.

[Reed-22] а ^б ^c ^d ^е Рид, Уильям Дж .; и другие. (2004). «Двойное логнормальное распределение Парето - новая параметрическая модель для распределений размеров». Коммуникации в статистике - теория и методы. 33 (8): 1733–53. CiteSeerX 10.1.1.70.4555. Дои:10.1081 / sta-120037438. S2CID 13906086.

[Reed2002-23] Рид, Уильям Дж. (2002). «О ранговом распределении населенных пунктов». Журнал региональной науки. 42 (1): 1–17. Дои:10.1111/1467-9787.00247. S2CID 154285730.

[24] Шредер, Бьянка; Дамур, Сотириос; Гилл, Филипа (24 февраля 2010 г.). «Понимание скрытых ошибок сектора и способы защиты от них» (PDF). 8-я конференция Usenix по файловым технологиям и технологиям хранения (FAST 2010). Получено 2010-09-10. Мы экспериментировали с 5 различными распределениями (геометрическим, Вейбулла, Рэлея, Парето и логнормальным), которые обычно используются в контексте надежности системы, и оценили их соответствие через общие квадраты разностей между фактической и предполагаемой частотами (χ² статистика). Мы последовательно обнаружили, что во всех моделях геометрическое распределение плохо согласуется, а распределение Парето дает наилучшее соответствие.

[Simon-25] Юджи Иджири; Саймон, Герберт А. (май 1975 г.). «Некоторые распределения, связанные со статистикой Бозе – Эйнштейна». Proc. Natl. Акад. Sci. Соединенные Штаты Америки. 72 (5): 1654–57. Bibcode:1975PNAS ... 72.1654I. Дои:10.1073 / pnas.72.5.1654. ЧВК 432601. PMID 16578724.

[26] Харчол-Балтер, Мор; Дауни, Аллен (август 1997 г.). «Использование распределений времени жизни процессов для динамической балансировки нагрузки» (PDF). ACM-транзакции в компьютерных системах. 15 (3): 253–258. Дои:10.1145/263326.263344. S2CID 52861447.

[27] Клейбер и Коц (2003): стр. 94.

[28] Сил, Х. (1980). «Вероятности выживания, основанные на распределении требований Парето». Бюллетень АСТИН. 11: 61–71. Дои:10.1017 / S0515036100006620.

[29] CumFreq, программное обеспечение для кумулятивного частотного анализа и подбора распределения вероятностей [1]

[30] Харди, Майкл (2010). «Закон Парето». Математический интеллигент. 32 (3): 38–43. Дои:10.1007 / s00283-010-9159-2. S2CID 121797873.

[31] «62 человека владеют тем же, что и половина мира, - говорится в отчете Oxfam Davos». Oxfam. Янв 2016.

[32] «Отчет о мировом благосостоянии за 2013 год». Credit Suisse. Октябрь 2013. с. 22. Архивировано из оригинал на 2015-02-14. Получено 2016-01-24.

[33] Танидзаки, Хисаши (2004). Вычислительные методы в статистике и эконометрике. CRC Press. п. 133. ISBN 9780824750886.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

Функция плотности вероятности Функции плотности вероятности Парето типа I для различных ${ displaystyle alpha}$ с участием ${ displaystyle x _ { mathrm {m}} = 1.}$ Так как ${ displaystyle alpha rightarrow infty,}$ подходы к распределению ${ displaystyle delta (х-х _ { mathrm {m}}),}$ где ${ displaystyle delta}$ это Дельта-функция Дирака.
Кумулятивная функция распределения Кумулятивные функции распределения Парето типа I для различных ${ displaystyle alpha}$ с участием ${ displaystyle x _ { mathrm {m}} = 1.}$
Параметры	${ displaystyle x _ { mathrm {m}}> 0}$ масштаб (настоящий ) ${ displaystyle alpha> 0}$ форма (реальный)
Поддержка	${ Displaystyle х в [х _ { mathrm {m}}, infty)}$
PDF	${ displaystyle { frac { alpha x _ { mathrm {m}} ^ { alpha}} {x ^ { alpha +1}}}}$
CDF	${ displaystyle 1- left ({ frac {x _ { mathrm {m}}} {x}} right) ^ { alpha}}$
Значить	${ displaystyle { begin {cases} infty & { text {for}} alpha leq 1 { dfrac { alpha x _ { mathrm {m}}} { alpha -1}} & { text {for}} alpha> 1 end {case}}}$
Медиана	${ displaystyle x _ { mathrm {m}} { sqrt [{ alpha}] {2}}}$
Режим	${ Displaystyle х _ { mathrm {m}}}$
Дисперсия	${ displaystyle { begin {cases} infty & { text {for}} alpha leq 2 { dfrac {x _ { mathrm {m}} ^ {2} alpha} {( alpha - 1) ^ {2} ( alpha -2)}} & { text {for}} alpha> 2 end {case}}}$
Асимметрия	${ displaystyle { frac {2 (1+ alpha)} { alpha -3}} { sqrt { frac { alpha -2} { alpha}}} { text {for}} alpha> 3}$
Ex. эксцесс	${ displaystyle { frac {6 ( alpha ^ {3} + alpha ^ {2} -6 alpha -2)} { alpha ( alpha -3) ( alpha -4)}} { text {for}} alpha> 4}$
Энтропия	${ displaystyle log left ( left ({ frac {x _ { mathrm {m}}} { alpha}} right) , e ^ {1 + { tfrac {1} { alpha}} }правильно)}$
MGF	${ displaystyle alpha (-x _ { mathrm {m}} t) ^ { alpha} Gamma (- alpha, -x _ { mathrm {m}} t) { text {for}} t <0 }$
CF	${ Displaystyle альфа (-ix _ { mathrm {m}} t) ^ { alpha} Gamma (- alpha, -ix _ { mathrm {m}} t)}$
Информация Fisher	${ Displaystyle { mathcal {I}} (х _ { mathrm {m}}, alpha) = { begin {bmatrix} { dfrac { alpha} {x _ { mathrm {m}} ^ {2} }} & - { dfrac {1} {x _ { mathrm {m}}}} - { dfrac {1} {x _ { mathrm {m}}}} & { dfrac {1} { альфа ^ {2}}} конец {bmatrix}}}$ Правильно: ${ Displaystyle { mathcal {I}} (х _ { mathrm {m}}, alpha) = { begin {bmatrix} { dfrac { alpha ^ {2}} {x _ { mathrm {m}} ^ {2}}} & 0 0 & { dfrac {1} { alpha ^ {2}}} end {bmatrix}}}$

Распределения вероятностей (Список )
Дискретный одномерный с конечной опорой	Бенфорд Бернулли бета-бином биномиальный категоричный гипергеометрический Бином Пуассона Радемахер солитон дискретная униформа Zipf Ципф – Мандельброт
Дискретный одномерный с бесконечной поддержкой	бета-отрицательный бином Борель Конвей – Максвелл – Пуассон дискретная фаза Делапорте расширенный отрицательный бином Флори-Шульц Гаусс – Кузьмин геометрический логарифмический отрицательный бином Panjer параболический фрактал Пуассон Скеллам Юл – Саймон Зета
Непрерывный одномерный поддерживается на ограниченном интервале	арксинус АРГУС Лысый – Николс Бейтс бета бета прямоугольный непрерывный Бернулли Ирвин – Холл Кумарасвами логит-нормальный нецентральная бета приподнятый косинус взаимный треугольный U-квадратичный униформа Полукруг Вигнера
Непрерывный одномерный поддерживается на полубесконечном интервале	Бенини Benktander 1-го рода Benktander 2-го рода бета прайм Заусенец хи-квадрат чи Дагум Дэвис экспоненциально-логарифмический Erlang экспоненциальный F сложенный нормальный Фреше гамма гамма / Gompertz обобщенная гамма обобщенный обратный гауссовский Гомпертц наполовину логистический наполовину нормальный Хотеллинга Т-квадрат гипер-Эрланг гиперэкспоненциальный гипоэкспоненциальный обратный хи-квадрат масштабированный обратный хи-квадрат обратный гауссовский обратная гамма Колмогоров Леви журнал-Коши лог-Лаплас логистика лог-нормальный Lomax матрично-экспоненциальный Максвелл – Больцманн Максвелл – Юттнер Mittag-Leffler Накагами нецентральный хи-квадрат нецентральный F Парето фазовый поли-Вейбулл Рэлей релятивистский Брейт – Вигнер Рис сдвинутый Гомпертц усеченный нормальный Тип-2 Гамбель Weibull дискретный Weibull Лямбда Уилкса
Непрерывный одномерный поддерживается на всей реальной линии	Коши экспоненциальная степень Фишера z Гауссовский q обобщенный нормальный обобщенный гиперболический геометрическая конюшня Гамбель Holtsmark гиперболический секанс Джонсона S_U Ландо Лаплас асимметричный лаплас логистика нецентральный т нормальный (гауссовский) нормально-обратный гауссовский перекос нормально слэш стабильный Ученики т Гамбель типа 1 Трейси – Уидом дисперсия-гамма Voigt
Непрерывный одномерный с поддержкой, тип которой варьируется	обобщенный хи-квадрат обобщенное экстремальное значение обобщенный Парето Марченко – Пастур q-экспоненциальный q-Гауссовский q-Вейбулл смещенная логистика Лямбда Тьюки
Смешанная непрерывно-дискретная одномерная	выпрямленный гауссовский
Многовариантный (совместный)	Дискретный Ewens полиномиальный Дирихле-полиномиальный отрицательный полиномиальный Непрерывный Дирихле обобщенный Дирихле многомерный Лаплас многомерный нормальный многомерный стабильный многомерный т нормальная обратная гамма нормальная гамма Матричнозначный обратная матрица гамма обратный-Wishart матрица нормальная матрица т матрица гамма нормальный-обратный-Уишарт нормальный-Wishart Wishart
Направленный	Одномерный (круговой) направленный Круглая форма одномерный фон Мизеса завернутый нормально завернутый Коши завернутый экспоненциальный обернутый асимметричный лаплас завернутый Леви Двумерный (сферический) Кент Двумерный (тороидальный) двумерный фон Мизеса Многомерный фон Мизес-Фишер Bingham
Вырожденный и единственное число	Вырожденный Дельта-функция Дирака Единственное число Кантор
Семьи	Круговой соединение Пуассона эллиптический экспоненциальный естественная экспонента расположение – масштаб максимальная энтропия смесь Пирсон Твиди завернутый

Параметры	${ displaystyle L> 0}$ расположение (настоящий ) ${ displaystyle H> L}$ расположение (настоящий ) ${ displaystyle alpha> 0}$ форма (реальный)
Поддержка	${ Displaystyle L leqslant х leqslant H}$
PDF	${ displaystyle { frac { alpha L ^ { alpha} x ^ {- alpha -1}} {1- left ({ frac {L} {H}} right) ^ { alpha}} }}$
CDF	${ displaystyle { frac {1-L ^ { alpha} x ^ {- alpha}} {1- left ({ frac {L} {H}} right) ^ { alpha}}}}$
Значить	${ displaystyle { frac {L ^ { alpha}} {1- left ({ frac {L} {H}} right) ^ { alpha}}} cdot left ({ frac { alpha} { alpha -1}} right) cdot left ({ frac {1} {L ^ { alpha -1}}} - { frac {1} {H ^ { alpha -1} }} right), alpha neq 1}$ ${ displaystyle { frac {{H} {L}} {{H} - {L}}} ln { frac {H} {L}}, alpha = 1}$
Медиана	${ displaystyle L left (1 - { frac {1} {2}} left (1- left ({ frac {L} {H}} right) ^ { alpha} right) right) ) ^ {- { frac {1} { alpha}}}}$
Дисперсия	${ displaystyle { frac {L ^ { alpha}} {1- left ({ frac {L} {H}} right) ^ { alpha}}} cdot left ({ frac { alpha} { alpha -2}} right) cdot left ({ frac {1} {L ^ { alpha -2}}} - { frac {1} {H ^ { alpha -2} }} right), alpha neq 2}$ ${ displaystyle { frac {2 {H} ^ {2} {L} ^ {2}} {{H} ^ {2} - {L} ^ {2}}} ln { frac {H} { L}}, alpha = 2}$ (это второй необработанный момент, а не дисперсия)
Асимметрия	${ displaystyle { frac {L ^ { alpha}} {1- left ({ frac {L} {H}} right) ^ { alpha}}} cdot { frac { alpha * ( L ^ {k- alpha} -H ^ {k- alpha})} {( alpha -k)}}, alpha neq j}$ (это k-й необработанный момент, а не перекос)