Типы сеток - Википедия - Types of mesh

А сетка представляет собой представление большей геометрической области меньшими дискретными ячейками. Сетки обычно используются для вычисления решений уравнения в частных производных и визуализировать компьютерная графика, а также для анализа географических и картографических данных. Сетка разделяет пространство на элементы (или же клетки или же зоны), над которым могут быть решены уравнения, которые затем аппроксимируют решение в большей области. Границы элементов могут быть ограничены внутренними или внешними границами модели. Элементы более высокого качества (имеющие лучшую форму) обладают лучшими числовыми характеристиками, где то, что составляет «лучший» элемент, зависит от общих управляющих уравнений и конкретного решения экземпляра модели.

Общие формы клеток

Двумерный

Основные двухмерные формы ячеек

Обычно используются два типа двумерных форм ячеек. Эти треугольник и четырехугольник.

Плохие с точки зрения вычислений элементы будут иметь резкие внутренние углы или короткие края, или и то, и другое.

Треугольник

Эта форма ячейки состоит из 3-х сторон и является одним из самых простых типов сетки. Треугольную сетку на поверхности всегда легко и быстро создать. Это наиболее распространено в неструктурированные сети.

Четырехугольник

Эта форма ячейки является базовой 4-х сторонней, как показано на рисунке. Чаще всего это встречается в структурированных сетках.

Четырехугольные элементы обычно исключаются из состояния или вогнутости.

Трехмерный

Основные трехмерные формы ячеек

Основным трехмерным элементом являются тетраэдр, четырехугольная пирамида, треугольная призма, и шестигранник. Все они имеют треугольные и четырехугольные грани.

Выдавленные двухмерные модели могут быть полностью представлены призмами и шестигранниками в виде выдавленных треугольников и четырехугольников.

В общем, четырехугольные грани в 3-х измерениях могут не быть идеально плоскими. Непланарную четырехугольную грань можно рассматривать как тонкий тетраэдрический объем, который разделяют два соседних элемента.

Тетраэдр

А тетраэдр имеет 4 вершины, 6 ребер и ограничен 4 треугольными гранями. В большинстве случаев сетка тетраэдрического объема может быть создана автоматически.

Пирамида

Четырехугольник пирамида имеет 5 вершин, 8 ребер, ограниченных 4 треугольными и 1 четырехугольной гранью. Они эффективно используются в качестве переходных элементов между квадратными и треугольными элементами граней и другими элементами в гибридных сетках и сетках.

Треугольная призма

А треугольная призма имеет 6 вершин, 9 ребер, ограниченных 2 треугольными и 3 четырехугольными гранями. Преимущество этого типа слоя заключается в том, что он эффективно разрешает пограничный слой.

Шестигранник

А шестигранник, топологический куб, имеет 8 вершин, 12 ребер, ограниченных 6 гранями четырехугольника. Его также называют шестнадцатеричный или кирпич.^[1] При том же количестве ячеек точность решений в гексаэдрических сетках наиболее высока.

Зоны пирамиды и треугольной призмы можно рассматривать в расчетах как вырожденные шестигранники, у которых некоторые ребра сведены к нулю. Также могут быть представлены другие вырожденные формы шестигранника.

Продвинутые клетки (многогранник)

А многогранник (двойственный) элемент имеет любое количество вершин, ребер и граней. Обычно требуется больше вычислительных операций на ячейку из-за количества соседей (обычно 10).^[2] Хотя это компенсируется точностью расчета.

Классификация сеток

Структурированная сетка

Неструктурированная сетка

Структурированные сетки

Структурированные сетки идентифицируются по регулярному подключению. Возможный выбор элементов - четырехугольник в 2D и шестигранник в 3D. Эта модель очень компактна, поскольку отношения соседства определяются организацией хранения. Некоторые другие преимущества структурированной сетки перед неструктурированной - лучшая сходимость и более высокое разрешение.^[3][4][5]

Неструктурированные сети

An неструктурированная сетка определяется по нерегулярному подключению. Его нелегко выразить как двумерный или трехмерный массив в памяти компьютера. Это позволяет использовать любой возможный элемент, который может использовать решатель. По сравнению со структурированными сетками эта модель может быть очень неэффективной, поскольку требует явного хранения отношений соседства. Эти сетки обычно используют треугольники в 2D и тетраэдрические в 3D.^[6]

Гибридные сетки

Гибридная сетка содержит как структурированные, так и неструктурированные участки. Он эффективно объединяет структурированные и неструктурированные сетки. Те части геометрии, которые являются регулярными, могут иметь структурированные сетки, а те, которые являются сложными, могут иметь неструктурированные сетки. Эти сетки могут быть неконформными, что означает, что линии сетки не должны совпадать на границах блоков.^[7]

Качество сетки

Считается, что сетка имеет более высокое качество, если более точное решение вычисляется быстрее. Точность и скорость находятся в напряжении. Уменьшение размера сетки всегда увеличивает точность, но также увеличивает затраты на вычисления.

Точность зависит как от ошибки дискретизации, так и от ошибки решения. Для ошибки дискретизации заданная сетка является дискретной аппроксимацией пространства и поэтому может обеспечить только приблизительное решение, даже если уравнения решены точно. (В компьютерной графике трассировка лучей количество выпущенных лучей является еще одним источником ошибки дискретизации.) Для ошибки решения для УЧП требуется много итераций по всей сетке. Расчет прерывается раньше, чем уравнения будут решены точно. Выбор типа элемента сетки влияет как на дискретизацию, так и на ошибку решения.

Точность зависит как от общего количества элементов, так и от формы отдельных элементов. Скорость каждой итерации растет (линейно) с количеством элементов, а количество необходимых итераций зависит от значения локального решения и градиента по сравнению с формой и размером локальных элементов.

Точность решения

Грубая сетка может обеспечить точное решение, если решение является постоянным, поэтому точность зависит от конкретного экземпляра проблемы. Можно выборочно уточнять сетку в областях, где градиенты решения высоки, тем самым повышая точность там. Точность, включая интерполированные значения внутри элемента, зависит от типа и формы элемента.

Скорость сходимости

Каждая итерация уменьшает ошибку между вычисленным и истинным решением. конвергенция означает меньшую ошибку с меньшим количеством итераций.

Сетка низкого качества может не учитывать важные элементы, такие как пограничный слой для потока жидкости. Ошибка дискретизации будет большой, и скорость сходимости ухудшится; решение может вообще не сходиться.

Независимость от сети

Решение считается независимым от сетки, если дискретизация и ошибка решения достаточно малы при достаточном количестве итераций. Это важно знать для сравнительных результатов. Исследование сходимости сетки состоит из уточнения элементов и сравнения уточненных решений с грубыми решениями. Если дальнейшее уточнение (или другие изменения) существенно не меняют решение, сетка является «независимой сеткой».

Выбор типа сетки

Асимметрия на основе равностороннего объема

Если точность важнее всего, то предпочтительнее использовать шестигранную сетку. Плотность сетки должна быть достаточно высокой, чтобы улавливать все особенности потока, но в то же время она не должна быть настолько высокой, чтобы захватывать ненужные детали потока, таким образом нагружая ЦП и тратя больше времени. Всякий раз, когда присутствует стена, сетка, прилегающая к стене, достаточно мелкая, чтобы разрешить поток пограничного слоя, и, как правило, четырехугольные, шестиугольные и призматические ячейки предпочтительнее, чем треугольники, тетраэдры и пирамиды. Квадратные и шестигранные ячейки могут быть растянуты, если поток полностью развит и одномерен.

Изображает перекос четырехугольника

На основе асимметрии, гладкости и соотношения сторон можно решить, подходит ли сетка.^[8]

Асимметрия

Асимметрия сетки является точным показателем качества и пригодности сетки. Большой перекос снижает точность интерполированных областей. Существует три метода определения перекоса сетки.

На основе равностороннего объема

Этот метод применим только к треугольникам и тетраэдрам и является методом по умолчанию.

${ displaystyle { text {Skewness}} = { frac { text {оптимальный размер ячейки - размер ячейки}} { text {оптимальный размер ячейки}}}}$

Плавное и большое изменение прыжка

По отклонению от нормированного равностороннего угла

Этот метод применим ко всем формам ячеек и граней и почти всегда используется для призм и пирамид.

${ displaystyle { text {Skewness (для квадрата)}} = max { left [{ frac { theta _ {max} -90} {90}}, { frac {90- theta _ { min}} {90}} right]}}$

Равноугольный перекос

Другой распространенный критерий качества основан на равноугольном перекосе.

${ displaystyle { text {Equiangle Skew}} = max { left [{ frac { theta _ {max} - theta _ {e}} {180- theta _ {e}}}, { гидроразрыв { theta _ {e} - theta _ {min}} { theta _ {e}}} right]}}$

куда:

${ displaystyle theta _ {max} ,}$ это самый большой угол в грани или ячейке,

${ Displaystyle theta _ {мин} ,}$ наименьший угол в грани или ячейке,

${ displaystyle theta _ {e} ,}$ - это угол для равноугловой грани или ячейки, т.е. 60 для треугольника и 90 для квадрата.

Асимметрия, равная 0, является наилучшей из возможных, а асимметрия, равная единице, почти никогда не является предпочтительной. Для шестнадцатеричных и четырехугольных ячеек асимметрия не должна превышать 0,85, чтобы получить достаточно точное решение.

Изображает изменения в соотношении сторон

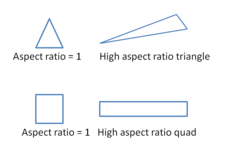
Для треугольных ячеек перекос не должен превышать 0,85, а для четырехугольных ячеек перекос не должен превышать 0,9.

Гладкость

Изменение размера также должно быть плавным. Не должно быть резких скачков размера ячейки, потому что это может привести к ошибочным результатам в соседних узлах.

Соотношение сторон

Это отношение самой длинной стороны ячейки к самой короткой. В идеале он должен быть равен 1 для обеспечения наилучших результатов. За многомерный поток, он должен быть близок к единице. Также локальные вариации в размере ячеек должны быть минимальными, т.е.размеры соседних ячеек не должны отличаться более чем на 20%. Имея большой соотношение сторон может привести к ошибке интерполяции неприемлемой величины.

Генерация и улучшение сетки

Смотрите также создание сетки и принципы построения сети В двух измерениях зеркальное отражение и сглаживание - мощные инструменты для адаптации плохой сетки к хорошей. Переворачивание включает объединение двух треугольников в четырехугольник, а затем разделение четырехугольника в другом направлении, чтобы получить два новых треугольника. Переворачивание используется для улучшения показателей качества треугольника, таких как перекос. Сглаживание сетки улучшает формы элементов и общее качество сетки за счет настройки расположения вершин сетки. При сглаживании сетки основные функции, такие как ненулевой узор линейная система сохраняются, поскольку топология сетки остается неизменной. Лапласовское сглаживание это наиболее часто используемый метод сглаживания.

Смотрите также

• Периодическая таблица конечных элементов
• Генерация сетки
• Неструктурированная сетка
• Обычная сетка
• Метод растянутой сетки

Рекомендации