Каноническая форма Вейра - Википедия - Weyr canonical form

На изображении показан пример общей матрицы Вейра, состоящей из двух блоков, каждый из которых является базовой матрицей Вейра. Основная матрица Вейра в верхнем левом углу имеет структуру (4,2,1), а другая - структуру (2,2,1,1).

В математика, в линейная алгебра, а Каноническая форма Вейра (или же, Форма Вейра или же Матрица Вейра) это квадратная матрица удовлетворяющие определенным условиям. Квадратная матрица называется в Вейр каноническая форма если матрица удовлетворяет условиям, определяющим каноническую форму Вейра. Форма Вейра была открыта Чешский математик Эдуард Вейр в 1885 г.^[1][2][3] Форма Вейра не стала популярной среди математиков, и ее затмила тесно связанная, но отличная каноническая форма, известная под названием Иорданская каноническая форма.^[3] Форма Вейра была открыта повторно несколько раз с момента первоначального открытия Вейра в 1885 году.^[4] Эту форму по-разному называли модифицированная форма Жордана, переупорядоченная форма Иордании, вторая форма Жордана, и H-форма.^[4] Нынешняя терминология приписывается Шапиро, который представил ее в статье, опубликованной в Американский математический ежемесячный журнал в 1999 году.^[4][5]

Недавно было найдено несколько приложений для матрицы Вейра. Особый интерес представляет применение матрицы Вейра для изучения филогенетические инварианты в биоматематика.

Определения

Базовая матрица Вейра

Определение

Базовая матрица Вейра с собственное значение ${ displaystyle lambda}$ является ${ Displaystyle п раз п}$ матрица ${ displaystyle W}$ следующего вида: Имеется раздел

${ displaystyle n_ {1} + n_ {2} + cdots + n_ {r} = n}$ из ${ displaystyle n}$ с ${ Displaystyle п_ {1} geq n_ {2} geq cdots geq n_ {r} geq 1}$

так что, когда ${ displaystyle W}$ рассматривается как ${ Displaystyle г раз г}$ блочная матрица ${ displaystyle (W_ {ij})}$, где ${ displaystyle (я, j)}$ блокировать ${ displaystyle W_ {ij}}$ является ${ displaystyle n_ {i} times n_ {j}}$ матрице присутствуют следующие три функции:

1. Главный диагональ блоки ${ displaystyle W_ {ii}}$ являются ${ Displaystyle п_ {я} раз п_ {я}}$ скалярные матрицы ${ displaystyle lambda I}$ за ${ Displaystyle я = 1, ldots, г}$.
2. Первый супердиагональ блоки ${ Displaystyle W_ {я, я + 1}}$ полны ранг столбца ${ Displaystyle п_ {я} раз п_ {я + 1}}$ матрицы в приведенная строчно-эшелонированная форма (то есть единичная матрица с последующими нулевыми строками) для ${ Displaystyle я = 1, ldots, г-1}$.
3. Все остальные блоки W равны нулю (то есть ${ displaystyle W_ {ij} = 0}$ когда ${ Displaystyle j neq я, я + 1}$).

В этом случае мы говорим, что ${ displaystyle W}$ имеет структуру Вейра ${ displaystyle (n_ {1}, n_ {2}, ldots, n_ {r})}$.

Пример

Ниже приводится пример базовой матрицы Вейра.

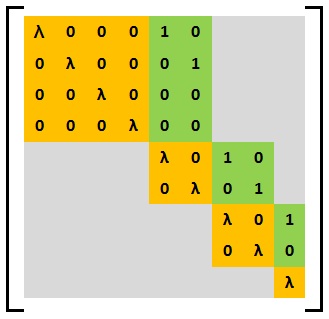
В этой матрице ${ displaystyle n = 9}$ и ${ displaystyle n_ {1} = 4, n_ {2} = 2, n_ {3} = 2, n_ {4} = 1}$. Так ${ displaystyle W}$ имеет структуру Вейра ${ Displaystyle (4,2,2,1)}$. Также,

и

Общая матрица Вейра

Определение

Позволять ${ displaystyle W}$ - квадратная матрица и пусть ${ displaystyle lambda _ {1}, ldots, lambda _ {k}}$ быть различными собственными значениями ${ displaystyle W}$. Мы говорим что ${ displaystyle W}$ находится в форме Вейра (или является матрицей Вейра), если ${ displaystyle W}$ имеет следующий вид:

куда ${ displaystyle W_ {i}}$ - базовая матрица Вейра с собственным значением ${ displaystyle lambda _ {я}}$ за ${ Displaystyle я = 1, ldots, к}$.

Пример

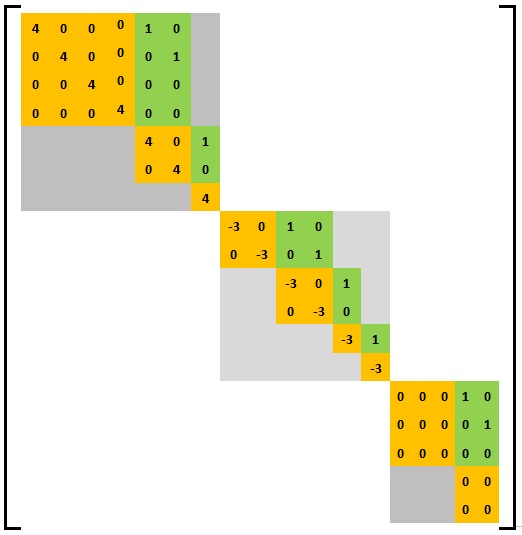
На следующем изображении показан пример общей матрицы Вейра, состоящей из трех основных блоков матрицы Вейра. Базовая матрица Вейра в верхнем левом углу имеет структуру (4,2,1) с собственным значением 4, средний блок имеет структуру (2,2,1,1) с собственным значением -3, а блок в правом нижнем углу угол имеет структуру (3, 2) с собственным значением 0.

Связь между формами Вейра и Иордании

Каноническая форма Вейра ${ displaystyle W = P ^ {- 1} JP}$ связана с жордановой формой ${ displaystyle J}$ простой перестановкой ${ displaystyle P}$ для каждого базового блока Вейра следующим образом: Первый индекс каждого подблока Вейра образует наибольшую цепочку Жордана. После вычеркивания этих строк и столбцов первый индекс каждого нового подблока образует вторую по величине цепочку Жордана и так далее.^[6]

Форма Вейра каноническая

То, что форма Вейра является канонической формой матрицы, является следствием следующего результата:^[3] Каждая квадратная матрица ${ displaystyle A}$ над алгебраически замкнутым полем аналогична матрице Вейра ${ displaystyle W}$ который уникален с точностью до перестановки его основных блоков. Матрица ${ displaystyle W}$ называется вейровской (канонической) формой ${ displaystyle A}$.

Вычисление канонической формы Вейра

Сведение к нильпотентному случаю

Позволять ${ displaystyle A}$ квадратная матрица порядка ${ displaystyle n}$ над алгебраически замкнутое поле и пусть различные собственные значения ${ displaystyle A}$ быть ${ displaystyle lambda _ {1}, lambda _ {2}, ldots, lambda _ {k}}$. В Разложение Жордана – Шевалле теорема утверждает, что ${ displaystyle A}$ является похожий к блочно-диагональной матрице вида

${ displaystyle A = { begin {bmatrix} lambda _ {1} I + N_ {1} &&& & lambda _ {2} I + N_ {2} && && ddots & &&& lambda _ {k} I + N_ {k} end {bmatrix}} = { begin {bmatrix} lambda _ {1} I &&& & lambda _ {2} I && && ddots & &&& lambda _ {k} I end {bmatrix}} + { begin {bmatrix} N_ {1} &&& & N_ {2} && && ddots & &&& N_ {k} end {bmatrix}} = D + N}$

куда ${ displaystyle D}$ это диагональная матрица, ${ displaystyle N}$ это нильпотентная матрица, и ${ displaystyle [D, N] = 0}$, оправдывая сокращение ${ displaystyle N}$ на подблоки ${ displaystyle N_ {i}}$. Итак, проблема сокращения ${ displaystyle A}$ к форме Вейра сводится к задаче приведения нильпотентных матриц ${ displaystyle N_ {i}}$ к форме Вейра. Это приводит к обобщенному собственное подпространство Теорема разложения.

Приведение нильпотентной матрицы к форме Вейра

Учитывая нильпотентную квадратную матрицу ${ displaystyle A}$ порядка ${ displaystyle n}$ над алгебраически замкнутым полем ${ displaystyle F}$, следующий алгоритм производит обратимую матрицу ${ displaystyle C}$ и матрица Вейра ${ displaystyle W}$ такой, что ${ Displaystyle W = C ^ {- 1} AC}$.

Шаг 1

Позволять ${ displaystyle A_ {1} = A}$

Шаг 2

1. Вычислить основа для пустое пространство из ${ displaystyle A_ {1}}$.
2. Расширить основу для нулевого пространства ${ displaystyle A_ {1}}$ к основе ${ displaystyle n}$-мерное векторное пространство ${ displaystyle F ^ {n}}$.
3. Сформировать матрицу ${ displaystyle P_ {1}}$ состоящий из этих базисных векторов.
4. Вычислить ${ displaystyle P_ {1} ^ {- 1} A_ {1} P_ {1} = { begin {bmatrix} 0 & B_ {2} 0 & A_ {2} end {bmatrix}}}$. ${ displaystyle A_ {2}}$ квадратная матрица размера ${ displaystyle n}$ - недействительность ${ displaystyle (A_ {1})}$.

Шаг 3

Если ${ displaystyle A_ {2}}$ не равно нулю, повторите шаг 2 на ${ displaystyle A_ {2}}$.

1. Вычислить основу для нулевого пространства ${ displaystyle A_ {2}}$.
2. Расширить основу для нулевого пространства ${ displaystyle A_ {2}}$ базису векторного пространства размерности ${ displaystyle n}$ - недействительность ${ displaystyle (A_ {1})}$.
3. Сформировать матрицу ${ displaystyle P_ {2}}$ состоящий из этих базисных векторов.
4. Вычислить ${ displaystyle P_ {2} ^ {- 1} A_ {2} P_ {2} = { begin {bmatrix} 0 & B_ {3} 0 & A_ {3} end {bmatrix}}}$. ${ displaystyle A_ {2}}$ квадратная матрица размера ${ displaystyle n}$ - недействительность ${ displaystyle (A_ {1})}$ - недействительность${ displaystyle (A_ {2})}$.

Шаг 4

Продолжайте процессы шагов 1 и 2, чтобы получить квадратные матрицы все меньшего размера. ${ Displaystyle A_ {1}, A_ {2}, A_ {3}, ldots}$ и связанные обратимые матрицы ${ Displaystyle P_ {1}, P_ {2}, P_ {3}, ldots}$ до первой нулевой матрицы ${ displaystyle A_ {r}}$ получается.

Шаг 5

Структура Вейра ${ displaystyle A}$ является ${ displaystyle (n_ {1}, n_ {2}, ldots, n_ {r})}$ куда ${ displaystyle n_ {i}}$ = недействительность${ displaystyle (A_ {i})}$.

Шаг 6

1. Вычислить матрицу ${ displaystyle P = P_ {1} { begin {bmatrix} I & 0 0 & P_ {2} end {bmatrix}} { begin {bmatrix} I & 0 0 & P_ {3} end {bmatrix}} cdots { begin {bmatrix} I & 0 0 & P_ {r} end {bmatrix}}}$ (здесь ${ displaystyle I}$являются идентичными матрицами подходящего размера).
2. Вычислить ${ Displaystyle X = P ^ {- 1} AP}$. ${ displaystyle X}$ представляет собой матрицу следующего вида:

${ displaystyle X = { begin {bmatrix} 0 & X_ {12} & X_ {13} & cdots & X_ {1, r-1} & X_ {1r} & 0 & X_ {23} & cdots & X_ {2, r-1 } & X_ {2r} &&& ddots & &&& cdots & 0 & X_ {r-1, r} &&&&& 0 end {bmatrix}}}$.

Шаг 7

Используйте элементарные операции со строками, чтобы найти обратимую матрицу ${ displaystyle Y_ {r-1}}$ подходящего размера, чтобы продукт ${ Displaystyle Y_ {r-1} X_ {r, r-1}}$ матрица вида ${ displaystyle I_ {r, r-1} = { begin {bmatrix} I O end {bmatrix}}}$.

Шаг 8

Набор ${ displaystyle Q_ {1} =}$ диагональ ${ displaystyle (I, I, ldots, Y_ {r-1} ^ {- 1}, I)}$ и вычислить ${ Displaystyle Q_ {1} ^ {- 1} XQ_ {1}}$. В этой матрице ${ Displaystyle (г, г-1)}$-блок есть ${ displaystyle I_ {r, r-1}}$.

Шаг 9

Найдите матрицу ${ displaystyle R_ {1}}$ сформированный как продукт элементарные матрицы такой, что ${ Displaystyle R_ {1} ^ {- 1} Q_ {1} ^ {- 1} XQ_ {1} R_ {1}}$ - матрица, в которой все блоки над блоком ${ displaystyle I_ {r, r-1}}$ содержать только ${ displaystyle 0}$с.

Шаг 10

Повторите шаги 8 и 9 для столбца ${ displaystyle r-1}$ преобразование ${ Displaystyle (г-1, г-2)}$-блокировать ${ displaystyle I_ {r-1, r-2}}$ через спряжение некоторой обратимой матрицей ${ displaystyle Q_ {2}}$. Используйте этот блок, чтобы очистить блоки, указанные выше, с помощью спряжения с помощью продукта ${ displaystyle R_ {2}}$ элементарных матриц.

Шаг 11

Повторите эти процессы на ${ Displaystyle г-2, г-3, ldots, 3,2}$ столбцы, используя спряжения по ${ Displaystyle Q_ {3}, R_ {3}, ldots, Q_ {r-2}, R_ {r-2}, Q_ {r-1}}$. Полученная матрица ${ displaystyle W}$ теперь в форме Вейра.

Шаг 12

Позволять ${ displaystyle C = P_ {1} { text {diag}} (I, P_ {2}) cdots { text {diag}} (I, P_ {r-1}) Q_ {1} R_ {1 } Q_ {2} cdots R_ {r-2} Q_ {r-1}}$. потом ${ Displaystyle W = C ^ {- 1} AC}$.

Приложения формы Вейра

Некоторые известные применения формы Вейра перечислены ниже:^[3]

1. Форму Вейра можно использовать для упрощения доказательства теоремы Герстенхабера, которая утверждает, что подалгебра, порожденная двумя коммутирующими ${ Displaystyle п раз п}$ матрицы имеют размерность не более ${ displaystyle n}$.
2. Набор конечных матриц называется приблизительно одновременно диагонализуемым, если они могут быть возмущены до одновременно диагонализуемых матриц. Форма Вейра используется для доказательства приближенной одновременной диагонализуемости различных классов матриц. Свойство приближенной одновременной диагонализуемости имеет приложения при изучении филогенетические инварианты в биоматематика.
3. Форму Вейра можно использовать для упрощения доказательств неприводимости многообразия всех k-наборы коммутирующих комплексных матриц.

Рекомендации