Приблизительное соответствие строк - Approximate string matching

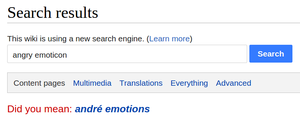
Нечеткий поиск Mediawiki по запросу "сердитый смайлик": "Вы имели в виду: Андре эмоции"

В Информатика, приблизительное соответствие строк (часто в просторечии называют поиск нечеткой строки) - это метод нахождения струны что соответствует шаблон приблизительно (а не точно). Проблема приблизительного сопоставления строк обычно делится на две подзадачи: поиск приблизительного подстрока совпадает с заданной строкой и находит словарные строки, примерно соответствующие шаблону.

Обзор

Близость совпадения измеряется количеством примитивных операций, необходимых для преобразования строки в точное совпадение. Этот номер называется редактировать расстояние между строкой и узором. Обычные примитивные операции:[1]

  • вставка: детская кроватка → coат
  • удаление: coат → детская кроватка
  • замена: coат → cosт

Эти три операции могут быть обобщены как формы подстановки путем добавления символа NULL (здесь обозначается *) везде, где символ был удален или вставлен:

  • вставка: co*т → coат
  • удаление: coат → co*т
  • замена: coат → cosт

Некоторые приближенные сопоставители также относятся к транспозиция, в котором позиции двух букв в строке меняются местами, что является примитивной операцией.[2]

  • транспозиция: coул → cots

Различные приближенные сопоставители накладывают разные ограничения. Некоторые сопоставители используют единую глобальную невзвешенную стоимость, то есть общее количество примитивных операций, необходимых для преобразования сопоставления в шаблон. Например, если узор катушка, фольга отличается одной заменой, катушки одной прошивкой, масло одним удалением, и жеребенок двумя заменами. Если все операции считаются одной единицей затрат и установлено ограничение на единицу, фольга, катушки, и масло будет считаться совпадением, пока жеребенок не буду.

Другие сопоставители определяют количество операций каждого типа отдельно, в то время как третьи устанавливают общую стоимость, но позволяют назначать разные веса разным операциям. Некоторые сопоставители позволяют раздельно присваивать пределы и веса отдельным группам в шаблоне.

Постановка проблемы и алгоритмы

Одно из возможных определений проблемы приблизительного сопоставления строк следующее: задана строка шаблона и текстовая строка , найдите подстроку в Т, который из всех подстрок Т, имеет наименьшее расстояние редактирования до шаблона п.

Подход грубой силы заключается в том, чтобы вычислить расстояние редактирования до P для всех подстрок T, а затем выбрать подстроку с минимальным расстоянием. Однако у этого алгоритма время работы О (п3 м).

Лучшее решение, которое предложили Продавцы[3], полагается на динамическое программирование. Используется альтернативная постановка задачи: для каждой позиции j в тексте Т и каждая позиция я в шаблоне п, вычислим минимальное расстояние редактирования между я первые символы узора, , и любая подстрока из Т что заканчивается на позиции j.

На каждую позицию j в тексте Т, и каждая позиция я в шаблоне п, пройдемся по всем подстрокам Т заканчивается в позиции j, и определить, какой из них имеет минимальное расстояние до я первые символы узора п. Запишите это минимальное расстояние как E(я, j). После вычисления E(я, j) для всех я и j, мы легко можем найти решение исходной задачи: это подстрока, для которой E(м, j) минимально (м длина рисунка п.)

Вычисление E(м, j) очень похож на вычисление расстояния редактирования между двумя строками. Фактически, мы можем использовать Алгоритм вычисления расстояния Левенштейна за E(м, j) с той лишь разницей, что мы должны инициализировать первую строку нулями и сохранить путь вычисления, то есть использовали ли мы E(я − 1,j), E (я,j - 1) или E(я − 1,j - 1) в вычислениях E(я, j).

В массиве, содержащем E(Икс, у) значения, затем выбираем минимальное значение в последней строке, пусть это будет E(Икс2, у2) и проследуйте по пути вычислений назад, обратно к строке номер 0. Если бы поле, к которому мы пришли, было E(0, у1), тогда Т[у1 + 1] ... Т[у2] - это подстрока T с минимальным расстоянием редактирования до шаблона п.

Вычисление E(Икс, у) массив принимает О (мин) время с алгоритмом динамического программирования, в то время как фаза обратной работы занимает О (п + м) время.

Еще одна недавняя идея - соединение подобия. Когда соответствующая база данных относится к большому объему данных, О (мин) время с алгоритмом динамического программирования не может работать в течение ограниченного времени. Итак, идея состоит в том, чтобы вместо вычисления сходства все пары строк, чтобы уменьшить количество пар-кандидатов. Широко используемые алгоритмы основаны на проверке фильтров, хешировании, Хеширование с учетом местоположения (LSH), Пытается и другие жадные и аппроксимационные алгоритмы. Большинство из них спроектировано так, чтобы соответствовать какой-либо структуре (например, Map-Reduce) для одновременных вычислений.

Он-лайн или оф-лайн

Традиционно алгоритмы приблизительного сопоставления строк подразделяются на две категории: оперативные и автономные. С помощью онлайн-алгоритмов шаблон может быть обработан перед поиском, а текст - нет. Другими словами, онлайн-методы выполняют поиск без индекса. Ранние алгоритмы для приблизительного сопоставления онлайн были предложены Вагнером и Фишером.[4] и продавцами[5]. Оба алгоритма основаны на динамическое программирование но решать разные проблемы. Алгоритм Продавца приблизительно ищет подстроку в тексте, в то время как алгоритм Вагнера и Фишера вычисляет Расстояние Левенштейна, подходит только для нечеткого поиска по словарю.

Методики онлайн-поиска неоднократно совершенствовались. Пожалуй, самое известное улучшение - это битовый алгоритм (также известный как алгоритм shift-or и shift-and), который очень эффективен для относительно коротких строк шаблона. Алгоритм Bitap - это сердце Unix поиск полезность соглашаться. Обзор алгоритмов онлайн-поиска был сделан Дж. Наварро.[6]

Хотя существуют очень быстрые интерактивные методы, их производительность на больших объемах данных неприемлема. Предварительная обработка текста или индексация значительно ускоряет поиск. Сегодня представлены различные алгоритмы индексации. Среди них есть суффиксные деревья[7], метрические деревья[8] и н-грамм методы.[9][10] Подробный обзор техник индексирования, позволяющих находить произвольную подстроку в тексте, дал Наварро. и другие.[11] Вычислительный обзор словарных методов (т.е. методов, позволяющих находить все словарные слова, приблизительно соответствующие поисковому шаблону) дан Бойцовым[12].

Приложения

Общие приложения приблизительного сопоставления включают: проверка орфографии.[13] При наличии большого количества данных ДНК сопоставление нуклеотид Последовательности стали важным приложением.[14] Приближенное соответствие также используется в фильтрация спама.[15] Запись связи это обычное приложение, в котором сопоставляются записи из двух разных баз данных.

Сопоставление строк нельзя использовать для большинства двоичных данных, таких как изображения и музыка. Для них требуются разные алгоритмы, например акустическая дактилоскопия.

Смотрите также

Рекомендации

  • ^ Baeza-Yates, R .; Наварро, Г. (июнь 1996 г.). «Более быстрый алгоритм приблизительного сопоставления строк». В Дэне Хирксберге; Джин Майерс (ред.). Комбинаторное сопоставление с образцом (CPM'96), LNCS 1075. Ирвин, Калифорния. С. 1–23. CiteSeerX  10.1.1.42.1593.
  • ^ Baeza-Yates, R .; Наварро, Г. «Быстрое приближенное сопоставление строк в словаре» (PDF). Proc. SPIRE'98. IEEE CS Press. С. 14–22.
  • ^ Бойцов, Леонид (2011). «Методы индексирования для приблизительного словарного поиска: сравнительный анализ». Журнал экспериментальной алгоритмики. 16 (1): 1–91. Дои:10.1145/1963190.1963191.
  • ^ Кормен, Томас; Лейзерсон, Ривест (2001). Введение в алгоритмы (2-е изд.). MIT Press. С. 364–7. ISBN  978-0-262-03293-3.
  • ^ Галил, Цви; Апостолико, Альберто (1997). Алгоритмы сопоставления с образцом. Оксфорд [Оксфордшир]: Издательство Оксфордского университета. ISBN  978-0-19-511367-9.
  • ^ Гасфилд, Дэн (1997). Алгоритмы на строках, деревьях и последовательностях: информатика и вычислительная биология. Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978-0-521-58519-4.
  • ^ Майерс, Г. (май 1999 г.). «Быстрый алгоритм бит-вектор для приблизительного сопоставления строк на основе динамического программирования» (PDF). Журнал ACM. 46 (3): 395–415. Дои:10.1145/316542.316550.
  • ^ Наварро, Гонсало (2001). «Экскурсия по приблизительному сопоставлению строк». Опросы ACM Computing. 33 (1): 31–88. CiteSeerX  10.1.1.96.7225. Дои:10.1145/375360.375365.
  • ^ Наварро, Гонсало; Баеза-Йейтс, Рикардо; Сутинен, Эркки; Тархио, Йорма (2001). «Методы индексирования для приблизительного сопоставления строк» (PDF). Бюллетень IEEE Data Engineering. 24 (4): 19–27.
  • ^ Продавцы, Питер Х. (1980). «Теория и вычисление эволюционных расстояний: распознавание образов». Журнал алгоритмов. 1 (4): 359–73. Дои:10.1016/0196-6774(80)90016-4.
  • ^ Скиена, Стив (1998). Руководство по разработке алгоритмов (1-е изд.). Springer. ISBN  978-0-387-94860-7.
  • ^ Укконен, Э. (1985). «Алгоритмы приблизительного сопоставления строк». Информация и контроль. 64 (1–3): 100–18. Дои:10.1016 / S0019-9958 (85) 80046-2.
  • ^ Вагнер, Р .; Фишер, М. (1974). «Проблема исправления строки в строку». Журнал ACM. 21: 168–73. Дои:10.1145/321796.321811.
  • ^ Зобель, Джастин; Дарт, Филипп (1995). «Нахождение примерных совпадений в больших лексиконах». Программное обеспечение - практика и опыт. 25 (3): 331–345. CiteSeerX  10.1.1.14.3856. Дои:10.1002 / spe.4380250307.

внешняя ссылка