Алгоритм Нидлмана – Вунша - Needleman–Wunsch algorithm
Эта статья может быть слишком техническим для большинства читателей, чтобы понять. Пожалуйста помогите улучшить это к сделать понятным для неспециалистов, не снимая технических деталей. (Сентябрь 2013) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Учебный класс | Выравнивание последовательности |
|---|---|
| Худший случай спектакль | |
| Худший случай космическая сложность |
В Алгоритм Нидлмана – Вунша является алгоритм используется в биоинформатика к выровнять белок или же нуклеотид последовательности. Это было одно из первых приложений динамическое программирование для сравнения биологических последовательностей. Алгоритм был разработан Солом Б. Нидлманом и Кристианом Д. Вуншем и опубликован в 1970 году.[1] Алгоритм по существу делит большую проблему (например, полную последовательность) на серию более мелких проблем и использует решения меньших проблем, чтобы найти оптимальное решение более крупной проблемы.[2] Его также иногда называют оптимальное соответствие алгоритм и глобальное выравнивание техника. Алгоритм Нидлмана – Вунша до сих пор широко используется для оптимального глобального выравнивания, особенно когда качество глобального выравнивания имеет первостепенное значение. Алгоритм присваивает оценку каждому возможному выравниванию, и цель алгоритма - найти все возможные выравнивания, имеющие наивысший балл.
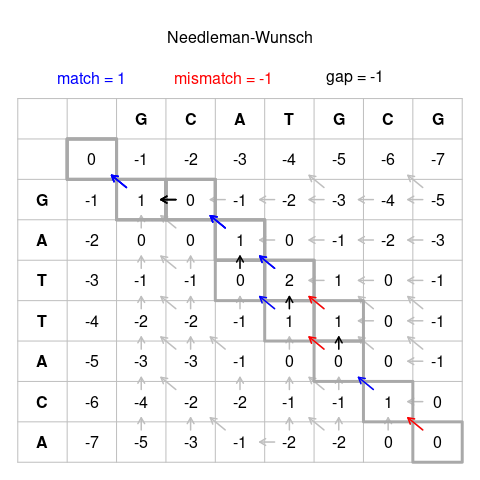
Результаты: Последовательности Наилучшее выравнивание --------- ---------------------- GCATGCU GCATG-CU GCA-TGCU GCAT-GCUGATTACA G-ATTACA G -ATTACA G-ATTACA Интерпретация шага инициализации: крайний левый столбец на приведенном выше рисунке можно интерпретировать следующим образом (помещая «дескриптор» перед каждой последовательностью, помеченной здесь как +): Выравнивание: + GCATGCU + GATTACAScore: 0 // Обработка совпадений обработчик, не набирает очков Выравнивание: + GCATGCU + GATTACAScore: 0 // 1 разрыв, оценка -1 Выравнивание: + GCATGCU + GATTACAScore: 0 // 2 разрыва, оценка -2 Выравнивание: + GCATGCU + GATTACAScore: 0 // 3 разрыва, score −3Alignment: + GCATGCU + GATTACAScore: 0 // 4 пробела, оценка −4 ... То же самое можно сделать для самой верхней строки.
Вступление
Этот алгоритм можно использовать для любых двух струны. В этом руководстве будут использоваться два небольших Последовательности ДНК в качестве примеров, как показано на схеме:
GCATGCUGATTACA
Построение сетки
Сначала постройте сетку, подобную показанной на рисунке 1 выше. Начните первую строку с вершины третьего столбца, а другую строку - с начала третьей строки. Заполните оставшиеся заголовки столбцов и строк, как показано на рисунке 1. В сетке еще не должно быть чисел.
| грамм | C | А | Т | грамм | C | U | ||
|---|---|---|---|---|---|---|---|---|
| грамм | ||||||||
| А | ||||||||
| Т | ||||||||
| Т | ||||||||
| А | ||||||||
| C | ||||||||
| А |
Выбор системы подсчета очков
Затем решите, как оценивать каждую отдельную пару букв. Используя приведенный выше пример, одним из возможных кандидатов на выравнивание может быть:
12345678
GCATG-CU
G-ATTACA
Буквы могут совпадать, не совпадать или совпадать с пробелом (удаление или вставка (индель )):
- Совпадение: две буквы в текущем индексе совпадают.
- Несоответствие: две буквы в текущем индексе разные.
- Indel (INsertion или DELetion): лучшее выравнивание предполагает выравнивание одной буквы по пробелу в другой строке.
Каждому из этих сценариев присваивается балл, а сумма баллов всех пар является баллом всего кандидата на выравнивание. Существуют разные системы для выставления оценок; некоторые были изложены в Системы подсчета очков раздел ниже. На данный момент система, используемая Нидлманом и Вуншем[1] будет использован:
- Матч: +1
- Несоответствие или несоответствие: -1
В приведенном выше примере оценка выравнивания будет равна 0:
GCATG-CU
G-ATTACA
+−++−−+− −> 1*4 + (−1)*4 = 0
Заполнение таблицы
Начните с нуля во второй строке второго столбца. Перемещайтесь по ячейкам строка за строкой, подсчитывая баллы для каждой ячейки. Оценка рассчитывается путем сравнения оценок ячеек, соседних с левой, верхней или верхней левой (диагональю) ячейки, и добавления соответствующей оценки за совпадение, несоответствие или отступ. Подсчитайте баллы кандидатов для каждой из трех возможностей:
- Путь от верхней или левой ячейки представляет собой пару отступов, поэтому возьмите баллы левой и верхней ячеек и добавьте баллы за отступы к каждой из них.
- Диагональный путь представляет совпадение / несоответствие, поэтому возьмите оценку левой верхней диагональной ячейки и добавьте оценку совпадения, если соответствующие основания (буквы) в строке и столбце совпадают, или оценку несоответствия, если нет.
Итоговая оценка ячейки является наивысшей из трех оценок кандидата.
Поскольку для второй строки нет «верхних» или «верхних левых» ячеек, только существующая ячейка слева может использоваться для вычисления оценки каждой ячейки. Следовательно, -1 добавляется для каждого сдвига вправо, поскольку это представляет собой отступ от предыдущей оценки. Это приводит к тому, что первая строка равна 0, -1, -2, -3, -4, -5, -6, -7. То же самое относится к первому столбцу, поскольку можно использовать только существующий счет над каждой ячейкой. Таким образом, итоговая таблица выглядит так:
| грамм | C | А | Т | грамм | C | U | ||
|---|---|---|---|---|---|---|---|---|
| 0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 | |
| грамм | −1 | |||||||
| А | −2 | |||||||
| Т | −3 | |||||||
| Т | −4 | |||||||
| А | −5 | |||||||
| C | −6 | |||||||
| А | −7 |
Первый случай с существующими оценками во всех 3 направлениях - это пересечение наших первых букв (в данном случае G и G). Окружающие клетки ниже:
| грамм | ||
|---|---|---|
| 0 | −1 | |
| грамм | −1 | Икс |
В этой ячейке есть три возможных суммы кандидатов:
- Сосед по диагонали в верхнем левом углу имеет счет 0. Соединение G и G является совпадением, поэтому сложите счет для совпадения: 0 + 1 = 1
- У верхнего соседа оценка -1, и перемещение оттуда представляет собой отступ, поэтому добавьте оценку для indel: (-1) + (-1) = (-2)
- Левый сосед также имеет оценку -1, представляет собой отступ и также дает (-2).
Наивысший кандидат равен 1 и вводится в ячейку:
| грамм | ||
|---|---|---|
| 0 | −1 | |
| грамм | −1 | 1 |
Также должна быть записана ячейка, которая дала кандидату наибольшее количество баллов. На завершенной диаграмме на рисунке 1 выше это представлено как стрелка от ячейки в строке и столбце 3 к ячейке в строке и столбце 2.
В следующем примере шаг по диагонали для X и Y представляет несоответствие:
| грамм | C | ||
|---|---|---|---|
| 0 | −1 | −2 | |
| грамм | −1 | 1 | Икс |
| А | −2 | Y |
ИКС:
- Вверху: (−2) + (- 1) = (−3)
- Слева: (+1) + (- 1) = (0)
- Вверху слева: (−1) + (- 1) = (−2)
Y:
- Сверху: (1) + (- 1) = (0)
- Слева: (−2) + (- 1) = (−3)
- Вверху слева: (−1) + (- 1) = (−2)
И для X, и для Y наивысший балл равен нулю:
| грамм | C | ||
|---|---|---|---|
| 0 | −1 | −2 | |
| грамм | −1 | 1 | 0 |
| А | −2 | 0 |
Наивысший балл кандидата может быть получен двумя или всеми соседними ячейками:
| Т | грамм | |
|---|---|---|
| Т | 1 | 1 |
| А | 0 | Икс |
- Сверху: (1) + (- 1) = (0)
- Вверху слева: (1) + (- 1) = (0)
- Слева: (0) + (- 1) = (−1)
В этом случае все направления, набравшие наибольшее количество баллов кандидата, должны быть отмечены как возможные исходные ячейки на готовой диаграмме на рисунке 1, например в ячейке в строке и столбце 7.
Заполнение таблицы таким образом дает оценки или всех возможных кандидатов на выравнивание, оценка в ячейке в правом нижнем углу представляет оценку выравнивания для наилучшего выравнивания.
Отслеживание стрелок назад к исходной точке
Отметьте путь от ячейки в правом нижнем углу до ячейки в левом верхнем углу, следуя направлению стрелок. С этого пути последовательность строится по следующим правилам:
- Диагональная стрелка представляет совпадение или несоответствие, поэтому буква столбца и буква строки исходной ячейки будут выровнены.
- Горизонтальная или вертикальная стрелка обозначает отступ. Горизонтальные стрелки выравнивают пробел ("-") с буквой строки ("боковая" последовательность), вертикальные стрелки выравнивают пробел с буквой столбца ("верхняя" последовательность).
- Если есть несколько стрелок для выбора, они представляют собой разветвление трасс. Если две или более ветки принадлежат путям от нижнего правого до верхнего левого угла ячейки, они одинаково жизнеспособны. В этом случае отметьте пути как отдельные кандидаты на выравнивание.
Следуя этим правилам, шаги для одного возможного кандидата на выравнивание на рисунке 1 следующие:
U → CU → GCU → -GCU → T-GCU → AT-GCU → CAT-GCU → GCAT-GCUA → CA → ACA → TACA → TTACA → ATTACA → -ATTACA → G-ATTACA ↓ (ветка) → TGCU → ... → TACA → ...
Системы подсчета очков
Базовые схемы подсчета очков
В простейших схемах подсчета очков просто указывается значение для каждого совпадения, несоответствия и отступа. В приведенном выше пошаговом руководстве используется match = 1, mismatch = −1, indel = −1. Таким образом, чем ниже оценка выравнивания, тем больше редактировать расстояние, для этой системы подсчета очков требуется высокий балл. Другая система подсчета очков может быть:
- Match = 0
- Indel = 1
- Несоответствие = 1
Для этой системы оценка выравнивания будет представлять собой расстояние редактирования между двумя строками. Для разных ситуаций могут быть разработаны различные системы подсчета очков, например, если пробелы считаются очень плохими для вашего выравнивания, вы можете использовать систему подсчета очков, которая сильно штрафует пробелы, например :
- Match = 0
- Несоответствие = 1
- Indel = 10
Матрица подобия
Более сложные системы подсчета присваивают значения не только типу изменения, но также и буквам, которые участвуют. Например, совпадению между A и A может быть присвоено 1, но совпадению между T и T может быть присвоено 4. Здесь (при условии первой системы подсчета очков) большее значение придается совпадению Ts, чем As, то есть совпадению Ts считается более важным для выравнивания. Это взвешивание по буквам также применяется к несоответствиям.
Для представления всех возможных комбинаций букв и их результирующих оценок используется матрица подобия. Матрица подобия для самой базовой системы представлена как:
| А | грамм | C | Т | |
|---|---|---|---|---|
| А | 1 | -1 | -1 | -1 |
| грамм | -1 | 1 | -1 | -1 |
| C | -1 | -1 | 1 | -1 |
| Т | -1 | -1 | -1 | 1 |
Каждая оценка представляет собой переход от одной буквы, соответствующей ячейке, к другой. Следовательно, здесь представлены все возможные совпадения и удаления (для алфавита ACGT). Обратите внимание, что все совпадения идут по диагонали, также не нужно заполнять всю таблицу, только этот треугольник, потому что оценки взаимны. = (Оценка для A → C = Оценка для C → A). При реализации правила T-T = 4 сверху получается следующая матрица подобия:
| А | грамм | C | Т | |
|---|---|---|---|---|
| А | 1 | −1 | −1 | −1 |
| грамм | −1 | 1 | −1 | −1 |
| C | −1 | −1 | 1 | −1 |
| Т | −1 | −1 | −1 | 4 |
Статистически построены разные скоринговые матрицы, которые придают вес различным действиям, подходящим для конкретного сценария. Наличие взвешенных оценочных матриц особенно важно при выравнивании белковых последовательностей из-за различной частоты встречаемости различных аминокислот. Существует два широких семейства скоринговых матриц, каждая из которых имеет дальнейшие изменения для конкретных сценариев:
Штраф за разрыв
При выравнивании последовательностей часто встречаются пробелы (т.е. инделки), иногда большие. С биологической точки зрения большой разрыв чаще возникает как одна большая делеция, чем как несколько отдельных делеций. Следовательно, две маленькие инделки должны иметь худшую оценку, чем одна большая. Простой и распространенный способ сделать это - использовать большой начальный балл для новой отступы и меньший балл за разрыв для каждой буквы, которая расширяет отступ. Например, new-indel может стоить -5, а extension-indel может стоить -1. Таким образом происходит выравнивание, такое как:
GAAAAAATG - A-A-T
который имеет несколько одинаковых выравниваний, некоторые с несколькими небольшими выравниваниями теперь будут выравниваться как:
ГААААААТГАА ---- Т
или любое выравнивание с 4 длинными промежутками предпочтительнее нескольких небольших промежутков.
Расширенное представление алгоритма
Баллы для выровненных символов указываются матрица сходства. Здесь, S(а, б) сходство персонажей а и б. Он использует линейный штраф за разрыв, здесь называется d.
Например, если матрица подобия была
| А | грамм | C | Т | |
|---|---|---|---|---|
| А | 10 | −1 | −3 | −4 |
| грамм | −1 | 7 | −5 | −3 |
| C | −3 | −5 | 9 | 0 |
| Т | −4 | −3 | 0 | 8 |
затем выравнивание:
AGACTAGTTACCGA --- GACGT
со штрафом за пропуск -5, будет иметь следующий счет:
- S(А, С) + S(G, G) + S(А, А) + (3 × d) + S(G, G) + S(Т, А) + S(Т, С) + S(А, G) + S(С, Т)
- = −3 + 7 + 10 − (3 × 5) + 7 + (−4) + 0 + (−1) + 0 = 1
Чтобы найти выравнивание с наивысшим баллом, двумерный множество (или же матрица ) F выделяется. Запись в строке я и столбец j обозначается здесь как. Для каждого символа в последовательности есть одна строка А, и один столбец для каждого символа в последовательности B. Таким образом, если выравнивание последовательностей размеров п и м, объем используемой памяти находится в . Алгоритм Хиршберга хранит в памяти только подмножество массива и использует пробел, но в остальном похож на Needleman-Wunsch (и по-прежнему требует время).
По мере продвижения алгоритма будет назначена оптимальная оценка для выравнивания первого персонажи в А и первый персонажи в B. В принцип оптимальности затем применяется следующим образом:
- Основа:
- Рекурсия, основанная на принципе оптимальности:
Таким образом, псевдокод для алгоритма вычисления матрицы F выглядит так:
d ← Очки штрафа за разрывза я = 0 к длина(А) F (i, 0) ← d * iза j = 0 к длина(Б) F (0, j) ← d * jза я = 1 к длина(А) за j = 1 к длина(B) {Match ← F (i − 1, j − 1) + S (Aя, Bj) Удалить ← F (i − 1, j) + d Вставить ← F (i, j − 1) + d F (i, j) ← Максимум(Сопоставить, Вставить, Удалить)}Однажды F матрица вычисляется, запись дает максимальный балл среди всех возможных раскладов. Чтобы вычислить выравнивание, которое фактически дает этот результат, вы начинаете с правой нижней ячейки и сравниваете значение с тремя возможными источниками (Match, Insert и Delete выше), чтобы увидеть, из какого оно получено. Если Match, то и выровнены, если Delete, то выравнивается с пробелом, а если Insert, то выравнивается с зазором. (Как правило, несколько вариантов могут иметь одно и то же значение, что приводит к альтернативным оптимальным согласованиям.)
ВыравниваниеA ← "" ВыравниваниеB ← "" i ← длина(А) j ← длина(В)пока (я> 0 или же j> 0) { если (я> 0 и j> 0 и F (i, j) == F (i − 1, j − 1) + S (Aя, Bj)) {AlignmentA ← Aя + ВыравниваниеA ВыравниваниеB ← Bj + ВыравниваниеB i ← i - 1 j ← j - 1} еще если (я> 0 и F (i, j) == F (i − 1, j) + d) {AlignmentA ← Aя + AlignmentA AlignmentB ← "-" + AlignmentB i ← i - 1} еще {AlignmentA ← "-" + AlignmentA AlignmentB ← Bj + AlignmentB j ← j - 1}}Сложность
Вычисление счета для каждой ячейки в таблице есть операция. Таким образом, временная сложность алгоритма для двух последовательностей длины и является .[3] Было показано, что можно улучшить время работы до с использованием Метод четырех русских.[3][4] Поскольку алгоритм заполняет таблица сложность пространства .[3]
Исторические заметки и разработка алгоритмов
Первоначальная цель алгоритма, описанного Нидлманом и Вуншем, состояла в том, чтобы найти сходство в аминокислотных последовательностях двух белков.[1]
Нидлман и Вунш подробно описывают свой алгоритм для случая, когда выравнивание наказывается исключительно совпадениями и несоответствиями, а за пропуски штраф не взимается (d= 0). В оригинальной публикации 1970 г. рекурсия.
Соответствующий алгоритм динамического программирования занимает кубическое время. В документе также указывается, что рекурсия может учитывать произвольные формулы штрафов за пробелы:
Фактор штрафа, число, вычитаемое за каждый пробел, может рассматриваться как препятствие для разрешения пробела. Штрафной коэффициент может зависеть от размера и / или направления зазора. [стр. 444]
Впервые был представлен лучший алгоритм динамического программирования с квадратичным временем выполнения для той же задачи (без штрафа за пропуски).[5] Дэвидом Санкоффом в 1972 г. Подобные квадратичные алгоритмы были открыты независимо Т. К. Винцюком.[6] в 1968 г. для обработки речи ("искривление времени" ), Робертом А. Вагнером и Майкл Дж. Фишер[7] в 1974 году для сопоставления строк.
Нидлман и Вунш сформулировали свою проблему в терминах максимального сходства. Другая возможность - минимизировать редактировать расстояние между последовательностями, введенными Владимир Левенштейн. Питер Х. Селлерс показал[8] в 1974 г., что эти две проблемы эквивалентны.
Алгоритм Нидлмана – Вунша до сих пор широко используется для оптимального глобальное выравнивание, особенно когда качество глобального согласования имеет первостепенное значение. Однако алгоритм является дорогостоящим с точки зрения времени и пространства, он пропорционален произведению длины двух последовательностей и, следовательно, не подходит для длинных последовательностей.
Недавние разработки были сосредоточены на улучшении временных и пространственных затрат алгоритма при сохранении качества. Например, в 2013 году алгоритм быстрого оптимального согласования глобальной последовательности (FOGSAA),[9] предложили выравнивание нуклеотидных / белковых последовательностей быстрее, чем другие оптимальные методы глобального выравнивания, включая алгоритм Нидлмана-Вунша. В документе утверждается, что по сравнению с алгоритмом Нидлмана – Вунша, FOGSAA обеспечивает выигрыш во времени на 70–90% для очень сходных нуклеотидных последовательностей (с подобием> 80%) и 54–70% для последовательностей, имеющих 30–80% сходства.
Инструменты глобального выравнивания с использованием алгоритма Нидлмана – Вунша
- Инструменты для глобального выравнивания игл EMBOSS и носилок EMBOSS
- Выравнивание Нидлмана-Вунша для двух нуклеотидных последовательностей
- MathWorks - глобальное выравнивание двух последовательностей с использованием алгоритма Нидлмана-Вунша
- BitKeeper - программное обеспечение для управления исходным кодом
Приложения за пределами биоинформатики
Компьютерное стереозрение
Стереосогласование - важный шаг в процессе 3D-реконструкции из пары стереоизображений. Когда изображения были исправлены, можно провести аналогию между выравниванием последовательностей нуклеотидов и белков и сопоставлением пиксели принадлежащий линии сканирования, поскольку обе задачи направлены на установление оптимального соответствия между двумя строками символов. «Правое» изображение стереопары можно рассматривать как видоизмененную версию «левого» изображения: шум и индивидуальная чувствительность камеры изменяют значения пикселей (т. Е. Подстановки символов); а другой угол обзора показывает ранее закрытые данные и вводит новые окклюзии (т.е. вставку и удаление символов). Как следствие, незначительные модификации алгоритма Нидлмана – Вунша делают его пригодным для стерео сопоставления.[10] Хотя характеристики с точки зрения точности не соответствуют последнему слову техники, относительная простота алгоритма позволяет его реализовать на встроенные системы.[11]
Хотя во многих приложениях можно выполнить исправление изображения, например к резекция камеры или калибровка, иногда это невозможно или непрактично, поскольку вычислительные затраты на точные модели выпрямления запрещают их использование в в реальном времени Приложения. Более того, ни одна из этих моделей не подходит, когда объектив камеры показывает неожиданное искажения, например, от капель дождя, непогоды или пыли. Расширяя алгоритм Нидлмана – Вунша, линия на «левом» изображении может быть связана с кривой на «правом» изображении путем нахождения совмещения с наивысшим баллом в трехмерном массиве (или матрице). Эксперименты показали, что такое расширение позволяет плотное совпадение пикселей между неректированными или искаженными изображениями.[12]
Смотрите также
- Алгоритм Вагнера – Фишера
- Алгоритм Смита – Уотермана
- Последовательный майнинг
- Расстояние Левенштейна
- Динамическое искажение времени
- Выравнивание последовательности
Рекомендации
- ^ а б c Нидлман, Сол Б. и Вунш, Кристиан Д. (1970). «Общий метод, применимый к поиску сходства в аминокислотной последовательности двух белков». Журнал молекулярной биологии. 48 (3): 443–53. Дои:10.1016/0022-2836(70)90057-4. PMID 5420325.
- ^ «биоинформатика». Получено 10 сентября 2014.
- ^ а б c Винг-кин., Сун (2010). Алгоритмы в биоинформатике: практическое введение. Бока-Ратон: Chapman & Hall / CRC Press. С. 34–35. ISBN 9781420070330. OCLC 429634761.
- ^ Масек, Уильям; Патерсон, Майкл (февраль 1980 г.). «Более быстрый алгоритм вычисления расстояний редактирования строк». Журнал компьютерных и системных наук. 20: 18–31. Дои:10.1016/0022-0000(80)90002-1.
- ^ Санкофф Д. (1972). «Соответствующие последовательности при ограничениях на удаление / вставку». Труды Национальной академии наук США. 69 (1): 4–6. Bibcode:1972ПНАС ... 69 .... 4С. Дои:10.1073 / pnas.69.1.4. ЧВК 427531. PMID 4500555.
- ^ Винцюк Т.К. (1968). «Распознавание речи с помощью динамического программирования». Кибернетика. 4: 81–88. Дои:10.1007 / BF01074755. S2CID 123081024.
- ^ Вагнер Р.А., Фишер М.Дж. (1974). «Проблема исправления строки в строку». Журнал ACM. 21 (1): 168–173. Дои:10.1145/321796.321811. S2CID 13381535.
- ^ Продавцы PH (1974). «К теории и вычислению эволюционных расстояний». Журнал SIAM по прикладной математике. 26 (4): 787–793. Дои:10.1137/0126070.
- ^ Чакраборти, Ангана; Bandyopadhyay, Sanghamitra (29 апреля 2013 г.). «FOGSAA: алгоритм быстрого оптимального глобального выравнивания последовательности». Научные отчеты. 3: 1746. Bibcode:2013НатСР ... 3E1746C. Дои:10.1038 / srep01746. ЧВК 3638164. PMID 23624407.
- ^ Дини Р., Тевенон Дж., Мартинес-дель-Ринкон Дж., Небель Дж .-К. (2011) "Алгоритм для стереоотношения, вдохновленный биоинформатикой ". Международная конференция по теории и приложениям компьютерного зрения, 5–7 марта, Виламура, Алгарве, Португалия.
- ^ Мадео С., Пелличча Р., Сальвадори К., Мартинес-дель-Ринкон Дж., Небель Х.-К. (2014) «Оптимизированная реализация стереозрения для встраиваемых систем: приложение к изображениям RGB и Infra-Red». Журнал обработки изображений в реальном времени ».
- ^ Тевенон, Дж; Мартинес-дель-Ринкон, Дж .; Dieny, R; Небель, Дж.С. (2012). Плотное сопоставление пикселей между не исправленными и искаженными изображениями с помощью динамического программирования. Международная конференция по теории и приложениям компьютерного зрения. Рим.
внешняя ссылка
Эта статья использование внешняя ссылка может не следовать политикам или рекомендациям Википедии. (Май 2017 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
- NW-align: программа выравнивания последовательности белков по алгоритму Нидлмана-Вунша (онлайн-сервер и исходный код)
- Параллельный алгоритм Нидлмана-Вунша для сетки - Осуществление Тахиром Навидом, Имитазом Саидом Сиддики и Шафтабом Ахмедом - Университет Бахрии
- Алгоритм Нидлмана-Вунша как код Haskell
- Живая демонстрация программы Needleman – Wunsch на основе Javascript
- Интерактивное визуальное объяснение алгоритма Нидлмана-Вунша на основе Javascript
- B.A.B.A. - апплет (с исходным кодом), который наглядно объясняет алгоритм.
- Четкое объяснение NW и его применения для выравнивания последовательностей
- Методы выравнивания последовательностей в блоге о технологиях
- Биостринги Пакет R, реализующий, среди прочего, алгоритм Нидлмана – Вунша
- Алгоритм Нидлмана-Вунша как код Haxe


















