Суффикс-автомат - Suffix automaton

Суффикс-автомат
Тип	Индекс подстроки
Изобрел	1983
Изобретенный	Ансельм Блумер; Джанет Блумер; Анджей Эренфойхт; Дэвид Хаусслер; Росс МакКоннелл
Сложность времени в нотация большой O
Алгоритм Средний Худший случай Космос ${ Displaystyle О (п)}$ ${ Displaystyle О (п)}$

В Информатика, а суффиксный автомат эффективный структура данных для представления индекс подстроки заданной строки, которая позволяет хранить, обрабатывать и извлекать сжатую информацию обо всех ее подстроки. Суффиксный автомат строки ${ displaystyle S}$ самый маленький ориентированный ациклический граф с выделенной начальной вершиной и набором «конечных» вершин, так что пути от начальной вершины к конечным вершинам представляют суффиксы строки. Формально суффиксный автомат определяется следующим набором свойств:

1. Его дуги помечены буквы;
2. ни один из его узлы иметь две исходящие дуги, помеченные одной и той же буквой;
3. для каждого суффикса ${ displaystyle S}$ существует путь от начальной вершины до некоторой конечной вершины такой, что конкатенация букв на пути образует этот суффикс;
4. у него наименьшее количество вершин среди всех графов, определенных указанными выше свойствами.

Говоря с точки зрения теория автоматов, суффиксный автомат - это минимальный частичный детерминированный конечный автомат который распознает набор суффиксы данного нить ${ displaystyle S = s_ {1} s_ {2} dots s_ {n}}$. В граф состояний суффиксного автомата называется ориентированным ациклическим графом слов (DAWG), термин, который также иногда используется для обозначения любого детерминированный ациклический конечный автомат.

Суффикс-автоматы были представлены в 1983 году группой ученых из Денверский университет и Университет Колорадо в Боулдере. Они предложили линейное время онлайн алгоритм для его построения и показал, что суффиксный автомат строки ${ displaystyle S}$ длина не менее двух символов не более ${ textstyle 2 | S | -1}$ государства и самое большее ${ textstyle 3 | S | -4}$ переходы. Дальнейшие работы показали тесную связь между суффиксными автоматами и суффиксные деревья, и обрисовали в общих чертах несколько обобщений суффиксных автоматов, таких как сжатый суффиксный автомат, полученный сжатием узлов с одной исходящей дугой.

Суффикс-автоматы обеспечивают эффективные решения таких проблем, как поиск подстроки и вычисление наибольшая общая подстрока из двух и более струн.

История

Ансельм Блюмер с рисунком обобщенного CDAWG для струнных ababc и abcab

Понятие суффиксного автомата было введено в 1983 году.^[1] группой ученых из Денверский университет и Университет Колорадо в Боулдере состоящий из Ансельма Блумера, Джанет Блумер, Анджей Эренфойхт, Дэвид Хаусслер и Росс МакКоннелл, хотя подобные концепции ранее изучались вместе с суффиксными деревьями в работах Питера Вайнера,^[2] Воан Пратт^[3] и Анатолий Слисенко.^[4] В своей первоначальной работе Блюмер и другие. показал суффиксный автомат, построенный для строки ${ displaystyle S}$ длины больше чем ${ displaystyle 1}$ имеет самое большее ${ displaystyle 2 | S | -1}$ государства и самое большее ${ displaystyle 3 | S | -4}$ переходов и предложил линейный алгоритм для построения автоматов.^[5]

В 1983 году Му-Тиан Чен и Джоэл Сейферас независимо показали, что алгоритм построения суффиксного дерева Вейнера 1973 года^[2] при построении суффиксного дерева строки ${ displaystyle S}$ строит суффиксный автомат перевернутой строки ${ textstyle S ^ {R}}$ как вспомогательная конструкция.^[6] В 1987 году Блюмер и другие. применил технику сжатия, используемую в суффиксных деревьях, к суффиксному автомату и изобрел сжатый суффиксный автомат, который также называют сжатым направленным ациклическим графом слов (CDAWG).^[7] В 1997 г. Максим Крочмор и Рено Верен разработали линейный алгоритм для прямого построения CDAWG.^[1] В 2001 году Сюнсуке Иненага и другие. разработал алгоритм построения CDAWG для набора слов, заданных три.^[8]

Определения

Обычно, говоря о суффиксных автоматах и ​​связанных с ними понятиях, некоторые понятия из формальная теория языка и теория автоматов используются, в частности:^[9]

• "Алфавит" конечный набор ${ displaystyle Sigma}$ который используется для построения слов. Его элементы называются «персонажами»;
• "Слово" конечная последовательность символов ${ displaystyle omega = omega _ {1} omega _ {2} dots omega _ {n}}$. «Длина» слова ${ displaystyle omega}$ обозначается как ${ displaystyle | omega | = n}$;
• "Формальный язык "- набор слов в заданном алфавите;
• «Язык всех слов» обозначается как ${ Displaystyle Sigma ^ {*}}$(где символ "*" означает Клини звезда ), «пустое слово» (слово нулевой длины) обозначается символом ${ displaystyle varepsilon}$;
• "Конкатенация слов " ${ Displaystyle альфа = альфа _ {1} альфа _ {2} точки альфа _ {п}}$ и ${ displaystyle beta = beta _ {1} beta _ {2} dots beta _ {m}}$ обозначается как ${ Displaystyle альфа cdot beta}$ или же ${ displaystyle alpha beta}$ и соответствует слову, полученному записью ${ displaystyle beta}$ справа от ${ displaystyle alpha}$, то есть, ${ displaystyle alpha beta = alpha _ {1} alpha _ {2} dots alpha _ {n} beta _ {1} beta _ {2} dots beta _ {m}}$;
• «Конкатенация языков» ${ displaystyle A}$ и ${ displaystyle B}$ обозначается как ${ Displaystyle A cdot B}$ или же ${ displaystyle AB}$ и соответствует набору попарных конкатенаций ${ Displaystyle AB = { alpha beta: alpha in A, beta in B }}$;
• Если слово ${ displaystyle omega in Sigma ^ {*}}$ может быть представлен как ${ Displaystyle омега = альфа гамма бета}$, куда ${ Displaystyle альфа, бета, гамма в Sigma ^ {*}}$, затем слова ${ displaystyle alpha}$, ${ displaystyle beta}$ и ${ displaystyle gamma}$ называются "префикс", "суффикс" и "подслово "(подстрока) слова ${ displaystyle omega}$ соответственно;
• Если ${ displaystyle T_ {l} T_ {l + 1} dots T_ {r} = S}$ тогда ${ displaystyle S}$ говорят, что "происходит" в ${ displaystyle T}$ как подслово. Здесь ${ displaystyle l}$ и ${ displaystyle r}$ называются левая и правая позиции вхождения ${ displaystyle S}$ в ${ displaystyle T}$ соответственно.

Структура автомата

Формально, детерминированный конечный автомат определяется 5-кратный ${ Displaystyle { mathcal {A}} = ( Sigma, Q, q_ {0}, F, delta)}$, куда:^[10]

• ${ displaystyle Sigma}$ это «алфавит», который используется для построения слов,
• ${ displaystyle Q}$ это набор автоматов "состояния ",
• ${ displaystyle q_ {0} in Q}$ - «начальное» состояние автомата,
• ${ Displaystyle F подмножество Q}$ набор «конечных» состояний автомата,
• ${ displaystyle delta: Q times Sigma mapsto Q}$ это частичный «переходная» функция автомата, такая, что ${ Displaystyle дельта (д, сигма)}$ за ${ displaystyle q in Q}$ и ${ displaystyle sigma in Sigma}$ либо не определено, либо определяет переход от ${ displaystyle q}$ над характером ${ displaystyle sigma}$.

Чаще всего детерминированный конечный автомат представляется в виде ориентированный граф («диаграмма») такая, что:^[10]

• Набор графа вершины соответствует состоянию состояний ${ displaystyle Q}$,
• График имеет конкретную отмеченную вершину, соответствующую начальному состоянию ${ displaystyle q_ {0}}$,
• График имеет несколько отмеченных вершин, соответствующих множеству конечных состояний ${ displaystyle F}$,
• Набор графика дуги соответствует набору переходов ${ displaystyle delta}$,
• В частности, каждый переход ${ textstyle delta (q_ {1}, sigma) = q_ {2}}$ представлен дугой из ${ displaystyle q_ {1}}$ к ${ displaystyle q_ {2}}$ отмечен символом ${ displaystyle sigma}$. Этот переход также можно обозначить как ${ textstyle q_ {1} { begin {smallmatrix} { sigma} [- 5pt] { longrightarrow} end {smallmatrix}} q_ {2}}$.

По диаграмме автомат распознает слово ${ displaystyle omega = omega _ {1} omega _ {2} dots omega _ {m}}$ только если есть путь из начальной вершины ${ displaystyle q_ {0}}$ в какую-то последнюю вершину ${ displaystyle q in F}$ так что объединение символов на этом пути образует ${ displaystyle omega}$. Набор слов, распознаваемых автоматом, образует язык, который должен распознаваться автоматом. В этих терминах язык, распознаваемый суффиксным автоматом ${ displaystyle S}$ это язык его (возможно, пустых) суффиксов.^[9]

Состояния автоматов

«Правильный контекст» слова ${ displaystyle omega}$ относительно языка ${ displaystyle L}$ это набор ${ displaystyle [ omega] _ {R} = { alpha: omega alpha in L }}$ это набор слов ${ displaystyle alpha}$ так что их соединение с ${ displaystyle omega}$ образует слово из ${ displaystyle L}$. Правильный контекст вызывает естественное отношение эквивалентности ${ displaystyle [ alpha] _ {R} = [ beta] _ {R}}$ по набору всех слов. Если язык ${ displaystyle L}$ распознается некоторым детерминированным конечным автоматом, существует единственное с точностью до изоморфизм автомат, который распознает тот же язык и имеет минимально возможное количество состояний. Такой автомат называется минимальный автомат для данного языка ${ displaystyle L}$. Теорема Майхилла – Нероде позволяет ему явно определять его с точки зрения правильного контекста:^[11][12]

В этих терминах «суффиксный автомат» - это минимальный детерминированный конечный автомат, распознающий язык суффиксов слова ${ displaystyle S = s_ {1} s_ {2} dots s_ {n}}$. Правильный контекст слова ${ displaystyle omega}$ по отношению к этому языку состоит из слов ${ displaystyle alpha}$, так что ${ displaystyle omega alpha}$ суффикс ${ displaystyle S}$. Это позволяет сформулировать следующую лемму, определяющую биекция между правым контекстом слова и набором правильных позиций его вхождений в ${ displaystyle S}$:^[13][14]

Например, для слова ${ displaystyle S = abacaba}$ и его подслово ${ displaystyle omega = ab}$, он держит ${ displaystyle endpos (ab) = {2,6 }}$ и ${ displaystyle [ab] _ {R} = {a, acaba }}$. Неофициально ${ displaystyle [ab] _ {R}}$ состоит из слов, следующих за вхождениями ${ displaystyle ab}$ до конца ${ displaystyle S}$ и ${ displaystyle endpos (ab)}$ формируется правильными позициями этих вхождений. В этом примере элемент ${ Displaystyle х = 2 in endpos (ab)}$ соответствует слову ${ displaystyle s_ {3} s_ {4} s_ {5} s_ {6} s_ {7} = acaba in [ab] _ {R}}$ в то время как слово ${ displaystyle a in [ab] _ {R}}$ соответствует элементу ${ displaystyle 7- | a | = 6 in endpos (ab)}$.

Из него следует несколько структурных свойств суффиксных состояний автомата. Позволять ${ Displaystyle | альфа | Leq | бета |}$, тогда:^[14]

• Если ${ displaystyle [ alpha] _ {R}}$ и ${ displaystyle [ beta] _ {R}}$ иметь хотя бы один общий элемент ${ displaystyle x}$, тогда ${ displaystyle endpos ( alpha)}$ и ${ displaystyle endpos ( beta)}$ также имеют общий элемент. Это подразумевает ${ displaystyle alpha}$ суффикс ${ displaystyle beta}$ и поэтому ${ displaystyle endpos ( beta) subset endpos ( alpha)}$ и ${ displaystyle [ beta] _ {R} subset [ alpha] _ {R}}$. В вышеупомянутом примере ${ displaystyle a in [ab] _ {R} cap [cab] _ {R}}$, так ${ displaystyle ab}$ суффикс ${ displaystyle cab}$ и поэтому ${ displaystyle [cab] _ {R} = {a } subset {a, acaba } = [ab] _ {R}}$ и ${ displaystyle endpos (cab) = {6 } subset {2,6 } = endpos (ab)}$;
• Если ${ displaystyle [ alpha] _ {R} = [ beta] _ {R}}$, тогда ${ Displaystyle endpos ( альфа) = endpos ( бета)}$, таким образом ${ displaystyle alpha}$ происходит в ${ displaystyle S}$ только как суффикс ${ displaystyle beta}$. Например, для ${ displaystyle alpha = b}$ и ${ displaystyle beta = ab}$ он считает, что ${ displaystyle [b] _ {R} = [ab] _ {R} = {a, acaba }}$ и ${ Displaystyle endpos (b) = endpos (ab) = {2,6 }}$;
• Если ${ displaystyle [ alpha] _ {R} = [ beta] _ {R}}$ и ${ displaystyle gamma}$ суффикс ${ displaystyle beta}$ такой, что ${ Displaystyle | альфа | Leq | гамма | Leq | бета |}$, тогда ${ displaystyle [ alpha] _ {R} = [ gamma] _ {R} = [ beta] _ {R}}$. В приведенном выше примере ${ displaystyle [c] _ {R} = [bac] _ {R} = {aba }}$ и это справедливо для "промежуточного" суффикса ${ displaystyle gamma = ac}$ который ${ displaystyle [ac] _ {R} = {aba }}$.

Любой штат ${ Displaystyle д = [ альфа] _ {R}}$ суффиксного автомата распознает некоторую непрерывную цепь вложенных суффиксов самого длинного слова, распознаваемого этим состоянием.^[14]

«Левое расширение» ${ Displaystyle { overset { scriptstyle { leftarrow}} { gamma}}}$ строки ${ displaystyle gamma}$ самая длинная строка ${ displaystyle omega}$ который имеет тот же правильный контекст, что и ${ displaystyle gamma}$. Длина ${ displaystyle | { overset { scriptstyle { leftarrow}} { gamma}} |}$ самой длинной строки, распознанной ${ Displaystyle д = [ гамма] _ {R}}$ обозначается ${ displaystyle len (q)}$. Он содержит:^[15]

«Суффиксная ссылка» ${ displaystyle ссылка (q)}$ государства ${ Displaystyle д = [ альфа] _ {R}}$ указатель на состояние ${ displaystyle p}$ который содержит самый большой суффикс ${ displaystyle alpha}$ что не признается ${ displaystyle q}$.

В этом смысле можно сказать ${ Displaystyle д = [ альфа] _ {R}}$ распознает точно все суффиксы ${ displaystyle { overset { scriptstyle { leftarrow}} { alpha}}}$ это дольше, чем ${ displaystyle len (ссылка (q))}$ и не дольше ${ displaystyle len (q)}$. Он также содержит:^[15]

Связь с суффиксными деревьями

Взаимосвязь дерева суффиксов, дерева суффиксов, DAWG и CDAWG

А "префиксное дерево "(или" дерево ") - корневое ориентированное дерево, в котором дуги помечены символами таким образом, чтобы не было вершин ${ displaystyle v}$ такого дерева имеет две выходящие дуги, отмеченные одним и тем же символом. Некоторые вершины в trie помечаются как конечные. Говорят, что Trie распознает набор слов, определяемых путями от его корня до конечных вершин. Таким образом, префиксные деревья представляют собой особый вид детерминированных конечных автоматов, если вы воспринимаете их корень как начальную вершину.^[16] "Суффикс трие" слова ${ displaystyle S}$ - это префиксное дерево, распознающее набор своих суффиксов. "А суффиксное дерево "представляет собой дерево, полученное из дерева суффиксов с помощью процедуры сжатия, во время которой последующие ребра объединяются, если степень вершины между ними равно двум.^[15]

По его определению, суффиксный автомат может быть получен через минимизация суффикса trie. Можно показать, что уплотненный суффиксный автомат получается как минимизацией суффиксного дерева (если предположить, что каждая строка на краю суффиксного дерева является сплошным символом из алфавита), так и уплотнением суффиксного автомата.^[17] Помимо этой связи между суффиксным деревом и суффиксным автоматом той же строки, существует также связь между суффиксным автоматом строки ${ displaystyle S = s_ {1} s_ {2} dots s_ {n}}$ и суффиксное дерево перевернутой строки ${ Displaystyle S ^ {R} = s_ {n} s_ {n-1} точки s_ {1}}$.^[18]

Аналогично правым контекстам можно ввести «левые контексты». ${ displaystyle [ omega] _ {L} = { beta in Sigma ^ {*}: beta omega in L }}$, "правильные расширения" ${ displaystyle { overset { scriptstyle { rightarrow}} { omega ~}}}$ соответствует самой длинной строке, имеющей тот же левый контекст, что и ${ displaystyle omega}$ и отношение эквивалентности ${ Displaystyle [ альфа] _ {L} = [ бета] _ {L}}$. Если учесть правильные расширения по отношению к языку ${ displaystyle L}$ "префиксов" строки ${ displaystyle S}$ можно получить:^[15]

, что подразумевает дерево суффиксных ссылок строки ${ displaystyle S}$ и суффиксное дерево строки ${ Displaystyle S ^ {R}}$ изоморфны:^[18]

Как и в случае левых расширений, для правых расширений верна следующая лемма:^[15]

Размер

Суффиксный автомат строки ${ displaystyle S}$ длины ${ displaystyle n> 1}$ имеет самое большее ${ displaystyle 2n-1}$ государства и самое большее ${ displaystyle 3n-4}$ переходы. Эти границы достигаются на строках ${ displaystyle abb dots bb = ab ^ {n-1}}$ и ${ displaystyle abb dots bc = ab ^ {n-2} c}$ соответственно.^[13] Это можно сформулировать более строго как ${ displaystyle | delta | leq | Q | + n-2}$ куда ${ displaystyle | delta |}$ и ${ displaystyle | Q |}$ - количество переходов и состояний в автомате соответственно.^[14]

Строительство

Первоначально автомат состоит только из одного состояния, соответствующего пустому слову, затем символы строки добавляются один за другим, и автомат постепенно перестраивается на каждом шаге.^[19]

Обновления состояния

После добавления нового символа к строке некоторые классы эквивалентности изменяются. Позволять ${ displaystyle [ alpha] _ {R _ { omega}}}$ быть правильным контекстом ${ displaystyle alpha}$ по отношению к языку ${ displaystyle omega}$ суффиксы. Тогда переход от ${ displaystyle [ alpha] _ {R _ { omega}}}$ к ${ displaystyle [ alpha] _ {R _ { omega x}}}$ после ${ displaystyle x}$ добавляется к ${ displaystyle omega}$ определяется леммой:^[14]

После добавления ${ displaystyle x}$ к текущему слову ${ displaystyle omega}$ правильный контекст ${ displaystyle alpha}$ может существенно измениться, только если ${ displaystyle alpha}$ суффикс ${ displaystyle omega x}$. Отсюда следует отношение эквивалентности ${ Displaystyle Equiv _ {R _ { omega x}}}$ это уточнение из ${ Displaystyle Equiv _ {R _ { omega}}}$. Другими словами, если ${ displaystyle [ alpha] _ {R _ { omega x}} = [ beta] _ {R _ { omega x}}}$, тогда ${ displaystyle [ alpha] _ {R _ { omega}} = [ beta] _ {R _ { omega}}}$. После добавления нового символа не более двух классов эквивалентности ${ Displaystyle Equiv _ {R _ { omega}}}$ будут разделены, и каждый из них может разделиться максимум на два новых класса. Во-первых, класс эквивалентности, соответствующий пустой правый контекст всегда разбивается на два класса эквивалентности, один из которых соответствует ${ displaystyle omega x}$ сам и имея ${ Displaystyle { varepsilon }}$ как правильный контекст. Этот новый класс эквивалентности содержит ровно ${ displaystyle omega x}$ и все его суффиксы, которых не было в ${ displaystyle omega}$, поскольку правый контекст таких слов раньше был пуст, а теперь содержит только пустое слово.^[14]

Зная соответствие между состояниями суффиксного автомата и вершинами суффиксного дерева, можно определить второе состояние, которое может расщепиться после добавления нового символа. Переход от ${ displaystyle omega}$ к ${ displaystyle omega x}$ соответствует переходу от ${ displaystyle omega ^ {R}}$ к ${ Displaystyle х omega ^ {R}}$ в перевернутой строке. В терминах суффиксных деревьев это соответствует вставке нового самого длинного суффикса ${ Displaystyle х omega ^ {R}}$ в суффиксное дерево ${ displaystyle omega ^ {R}}$. После такой вставки могут образоваться не более двух новых вершин: одна из них соответствует ${ Displaystyle х omega ^ {R}}$, а другой соответствует своему прямому предку, если было ветвление. Возвращаясь к суффиксным автоматам, это означает, что первое новое состояние распознает ${ displaystyle omega x}$ а второй (если есть второе новое состояние) - его суффиксная ссылка. Это можно сформулировать в виде леммы:^[14]

Это означает, что если ${ Displaystyle альфа = бета}$ (например, когда ${ displaystyle x}$ не произошло в ${ displaystyle omega}$ вообще и ${ Displaystyle альфа = бета = varepsilon}$), то разбивается только класс эквивалентности, соответствующий пустому правому контексту.^[14]

Помимо суффиксных ссылок необходимо также определить конечные состояния автомата. Из свойств структуры следует, что все суффиксы слова ${ displaystyle alpha}$ признанный ${ Displaystyle д = [ альфа] _ {R}}$ распознаются некоторой вершиной на суффикс путь ${ Displaystyle (д, ссылка (д), ссылка ^ {2} (д), точки)}$ из ${ displaystyle q}$. А именно, суффиксы длиной больше, чем ${ displaystyle len (ссылка (q))}$ роды ${ displaystyle q}$, суффиксы длиной больше, чем ${ displaystyle len (ссылка (ссылка (q))}$ но не больше чем ${ displaystyle len (ссылка (q))}$ роды ${ displaystyle ссылка (q)}$ и так далее. Таким образом, если государство, признающее ${ displaystyle omega}$ обозначается ${ displaystyle last}$, то все конечные состояния (то есть распознавание суффиксов ${ displaystyle omega}$) образуют последовательность ${ displaystyle (последняя, ​​ссылка (последняя), ссылка ^ {2} (последняя), точки)}$.^[19]

Обновления переходов и суффиксных ссылок

После персонажа ${ displaystyle x}$ добавляется к ${ displaystyle omega}$ возможные новые состояния суффиксного автомата ${ displaystyle [ omega x] _ {R _ { omega x}}}$ и ${ displaystyle [ alpha] _ {R _ { omega x}}}$. Суффиксная ссылка от ${ displaystyle [ omega x] _ {R _ { omega x}}}$ идет в ${ displaystyle [ alpha] _ {R _ { omega x}}}$ и из ${ displaystyle [ alpha] _ {R _ { omega x}}}$ это идет к ${ displaystyle ссылка ([ alpha] _ {R _ { omega}})}$. Слова из ${ displaystyle [ omega x] _ {R _ { omega x}}}$ происходить в ${ displaystyle omega x}$ только в качестве его суффиксов, поэтому вообще не должно быть переходов от ${ displaystyle [ omega x] _ {R _ { omega x}}}$ а переходы к нему должны идти от суффиксов ${ displaystyle omega}$ иметь длину не менее ${ displaystyle alpha}$ и быть отмеченным символом ${ displaystyle x}$. Состояние ${ displaystyle [ alpha] _ {R _ { omega x}}}$ формируется подмножеством ${ displaystyle [ alpha] _ {R _ { omega}}}$, таким образом, переход от ${ displaystyle [ alpha] _ {R _ { omega x}}}$ должно быть таким же, как от ${ displaystyle [ alpha] _ {R _ { omega}}}$. Между тем переходы, ведущие к ${ displaystyle [ alpha] _ {R _ { omega x}}}$ должен идти от суффиксов ${ displaystyle omega}$ имеющий длину меньше чем ${ Displaystyle | альфа |}$ и по крайней мере ${ displaystyle len (ссылка ([ alpha] _ {R _ { omega}}))}$, поскольку такие переходы привели к ${ displaystyle [ alpha] _ {R _ { omega}}}$ раньше и соответствовал отделившейся части этого государства. Состояния, соответствующие этим суффиксам, могут быть определены путем обхода пути ссылки суффикса для ${ displaystyle [ omega] _ {R _ { omega}}}$.^[19]

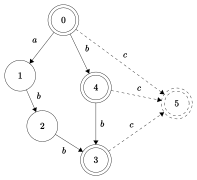
Построение суффиксного автомата для слова abbcbc
∅ → а После добавления первого символа в автомате суффикса создается только одно состояние. Точно так же к суффиксному дереву добавляется только один лист.	а → ab Новые переходы выводятся из всех предыдущих конечных состояний как б не появлялся раньше. По той же причине к корню суффиксного дерева добавляется еще один лист.
ab → abb Состояние 2 распознает слова ab и б, но только б - новый суффикс, поэтому это слово разделяется на состояние 4. В суффиксном дереве это соответствует расщеплению ребра, ведущего в вершину 2.	abb → abbc Характер c происходит впервые, поэтому переходы выполняются из всех предыдущих конечных состояний. Дерево суффиксов обратной строки имеет еще один лист, добавленный к корню.
abbc → abbcb Состояние 4 состоит из единственного слова б, который является суффиксом, поэтому состояние не разбивается. Соответственно, новый лист навешивается на вершину 4 суффиксного дерева.	abbcb → abbcbc Состояние 5 распознает слова abbc, BBC, до н.э и c, но только последние два являются суффиксами нового слова, поэтому они разделяются на новое состояние 8. Соответственно, ребро, ведущее к вершине 5, разбивается, а вершина 8 помещается в середину ребра.

Алгоритм построения

Теоретические результаты, приведенные выше, приводят к следующему алгоритму, который принимает характер ${ displaystyle x}$ и восстанавливает суффиксный автомат ${ displaystyle omega}$ в суффиксный автомат ${ displaystyle omega x}$:^[19]

1. Состояние, соответствующее слову ${ displaystyle omega}$ хранится как ${ displaystyle last}$;
2. После ${ displaystyle x}$ добавляется предыдущее значение ${ displaystyle last}$ хранится в переменной ${ displaystyle p}$ и ${ displaystyle last}$ сам переназначен в новое состояние, соответствующее ${ displaystyle omega x}$;
3. Состояния, соответствующие суффиксам ${ displaystyle omega}$ обновляются переходами на ${ displaystyle last}$. Для этого нужно пройти ${ displaystyle p, ссылка (p), ссылка ^ {2} (p), dots}$, пока не появится состояние, в котором уже есть переход на ${ displaystyle x}$;
4. По окончании вышеупомянутого цикла возможны 3 случая:
   1. Если ни одно из состояний на пути суффикса не имело перехода на ${ displaystyle x}$, тогда ${ displaystyle x}$ никогда не происходило в ${ displaystyle omega}$ до и суффиксная ссылка из ${ displaystyle last}$ должен привести к ${ displaystyle q_ {0}}$;
   2. Если переход по ${ displaystyle x}$ находится и ведет от государства ${ displaystyle p}$ государству ${ displaystyle q}$, так что ${ displaystyle len (p) + 1 = len (q)}$, тогда ${ displaystyle q}$ не нужно разделять, и это суффиксная ссылка ${ displaystyle last}$;
   3. Если переход найден, но ${ displaystyle len (q)> len (p) +1}$, затем слова из ${ displaystyle q}$ иметь длину не более ${ displaystyle len (p) +1}$ следует выделить в новое состояние «клон» ${ displaystyle cl}$;
5. Если предыдущий шаг был завершен созданием ${ displaystyle cl}$, переходы от него и его суффиксная ссылка должны копировать переходы от ${ displaystyle q}$, в то же время ${ displaystyle cl}$ назначается как общее суффиксное звено обоих ${ displaystyle q}$ и ${ displaystyle last}$;
6. Переходы, которые привели к ${ displaystyle q}$ раньше, но соответствовало словам длины не более ${ displaystyle len (p) +1}$ перенаправлены на ${ displaystyle cl}$. Для этого нужно пройти суффиксный путь ${ displaystyle p}$ пока не будет найдено состояние, при котором переход по ${ displaystyle x}$ от этого не ведет к ${ displaystyle q}$.

Вся процедура описывается следующим псевдокодом:^[19]

функция add_letter (x):    определять p = последний    назначать last = new_state ()    назначать len (последняя) = len (p) + 1    пока δ (р, х) не определено: назначать δ (p, x) = последняя, ​​p = ссылка (p)    определять д = δ (р, х)    если q = последний:        назначать ссылка (последняя) = q0    иначе если len (q) = len (p) + 1:        назначать ссылка (последняя) = q    еще:        определять cl = new_state ()        назначать len (cl) = len (p) + 1        назначать δ (cl) = δ (q), ссылка (cl) = ссылка (q)        назначать ссылка (последняя) = ссылка (q) = cl        пока δ (p, x) = q:            назначать δ (p, x) = cl, p = ссылка (p)

Здесь ${ displaystyle q_ {0}}$ - начальное состояние автомата и ${ displaystyle new _state ()}$ это функция, создающая для него новое состояние. Предполагается ${ displaystyle last}$, ${ displaystyle len}$, ${ displaystyle link}$ и ${ displaystyle delta}$ хранятся как глобальные переменные.^[19]

Сложность

Сложность алгоритма может варьироваться в зависимости от базовой структуры, используемой для хранения переходов автомата. Это может быть реализовано в ${ Displaystyle О (п журнал | Sigma |)}$ с ${ Displaystyle О (п)}$ накладные расходы памяти или в ${ Displaystyle О (п)}$ с ${ Displaystyle О (п | Sigma |)}$ накладные расходы на память, если предполагается, что выделение памяти выполняется в ${ Displaystyle O (1)}$. Чтобы получить такую ​​сложность, необходимо использовать методы амортизированный анализ. Значение ${ displaystyle len (p)}$ строго уменьшается с каждой итерацией цикла, в то время как он может увеличиваться только на единицу после первой итерации цикла на следующей add_letter вызов. Общая стоимость ${ displaystyle len (p)}$ никогда не превышает ${ displaystyle n}$ и он увеличивается только на единицу между итерациями добавления новых букв, что предполагает, что общая сложность также является не более чем линейной. Аналогично демонстрируется линейность второго цикла.^[19]

Обобщения

Суффиксный автомат тесно связан с другими суффиксными структурами и индексы подстроки. Имея суффиксный автомат конкретной строки, можно построить ее суффиксное дерево с помощью сжатия и рекурсивного обхода за линейное время.^[20] Подобные преобразования возможны в обоих направлениях для переключения между суффиксным автоматом ${ displaystyle S}$ и суффиксное дерево перевернутой строки ${ Displaystyle S ^ {R}}$.^[18] Помимо этого, было разработано несколько обобщений для построения автомата для набора строк, заданных trie,^[8] компактная суффиксная автоматизация (CDAWG),^[7] сохранить структуру автомата на скользящем окне,^[21] и строить его двунаправленным способом, поддерживая вставку символов как в начало, так и в конец строки.^[22]

Сжатый суффикс-автомат

Как уже упоминалось выше, уплотненный суффиксный автомат получается как посредством уплотнения регулярного суффиксного автомата (путем удаления состояний, которые не являются конечными и имеют ровно одну выходящую дугу), так и посредством минимизации суффиксного дерева. Как и в случае обычного суффиксного автомата, состояния уплотненного суффиксного автомата могут быть определены явно. Двустороннее расширение ${ displaystyle { overset { scriptstyle { longleftrightarrow}} { gamma}}}$ слова ${ displaystyle gamma}$ это самое длинное слово ${ Displaystyle омега = бета гамма альфа}$, так что каждое вхождение ${ displaystyle gamma}$ в ${ displaystyle S}$ предшествует ${ displaystyle beta}$ и ему удалось ${ displaystyle alpha}$. В терминах левого и правого расширений это означает, что двустороннее расширение - это левое расширение правого расширения или, что эквивалентно, правое расширение левого расширения, то есть ${ textstyle { overset { scriptstyle longleftrightarrow} { gamma}} = { overset { scriptstyle leftarrow} { overset { rightarrow} { gamma}}} = { overset { rightarrow} { overset { scriptstyle leftarrow} { gamma}}}}$. В терминах двустороннего расширения компактный автомат определяется следующим образом:^[15]

Двусторонние расширения индуцируют отношение эквивалентности ${ textstyle { overset { scriptstyle longleftrightarrow} { alpha}} = { overset { scriptstyle longleftrightarrow} { beta}}}$ который определяет набор слов, распознаваемых одним и тем же состоянием уплотненного автомата. Это отношение эквивалентности является переходное закрытие отношения, определяемого ${ textstyle ({ overset { scriptstyle { rightarrow}} { alpha ,}} = { overset { scriptstyle { rightarrow}} { beta ,}}) vee ({ overset { стиль сценария { leftarrow}} { alpha}} = { overset { scriptstyle { leftarrow}} { beta}})}$, что подчеркивает тот факт, что компактный автомат может быть получен склейкой эквивалентных вершин суффиксного дерева через ${ displaystyle { overset { scriptstyle { leftarrow}} { alpha}} = { overset { scriptstyle { leftarrow}} { beta}}}$ отношения (минимизация суффиксного дерева) и состояний суффиксного автомата склейки эквивалентны через ${ Displaystyle { overset { scriptstyle { rightarrow}} { alpha ,}} = { overset { scriptstyle { rightarrow}} { beta ,}}}$ отношение (уплотнение суффиксного автомата).^[23] Если слова ${ displaystyle alpha}$ и ${ displaystyle beta}$ имеют такие же правильные расширения и слова ${ displaystyle beta}$ и ${ displaystyle gamma}$ имеют одинаковые левые расширения, затем все строки в совокупности ${ displaystyle alpha}$, ${ displaystyle beta}$ и ${ displaystyle gamma}$ имеют такие же двусторонние расширения. В то же время может случиться так, что ни левое, ни правое продолжение ${ displaystyle alpha}$ и ${ displaystyle gamma}$ совпадают. В качестве примера можно взять ${ Displaystyle S = бета = ab}$, ${ Displaystyle альфа = а}$ и ${ displaystyle gamma = b}$, для которых левое и правое расширение следующие: ${ Displaystyle { overset { scriptstyle { rightarrow}} { alpha ,}} = { overset { scriptstyle { rightarrow}} { beta ,}} = ab = { overset { scriptstyle { leftarrow}} { beta}} = { overset { scriptstyle { leftarrow}} { gamma}}}$, но ${ displaystyle { overset { scriptstyle { rightarrow}} { gamma ,}} = b}$ и ${ Displaystyle { overset { scriptstyle { leftarrow}} { alpha}} = а}$. При этом, в то время как отношения эквивалентности односторонних расширений были сформированы некоторой непрерывной цепочкой вложенных префиксов или суффиксов, отношения эквивалентности двусторонних расширений более сложны, и единственное, что можно сделать с уверенностью, это то, что строки с одинаковым двусторонним расширением находятся подстроки самой длинной строки с одинаковым двусторонним расширением, но может даже случиться так, что у них нет общей непустой подстроки. Общее количество классов эквивалентности для этого отношения не превышает ${ displaystyle n + 1}$ откуда следует, что сжатый суффикс-автомат строки длины ${ displaystyle n}$ имеет самое большее ${ displaystyle n + 1}$ состояния. Количество переходов в таком автомате не более ${ displaystyle 2n-2}$.^[15]

Суффиксный автомат из нескольких строк

Рассмотрим набор слов ${ Displaystyle Т = {S_ {1}, S_ {2}, точки, S_ {k} }}$. Можно построить обобщение суффиксного автомата, которое распознало бы язык, образованный суффиксами всех слов из набора. Ограничения на количество состояний и переходов в таком автомате останутся такими же, как и для однословного автомата, если вы положите ${ Displaystyle п = | S_ {1} | + | S_ {2} | + точки + | S_ {k} |}$.^[23] Алгоритм аналогичен построению однословного автомата, но вместо ${ displaystyle last}$ состояние, функция add_letter будет работать с состоянием, соответствующим слову ${ displaystyle omega _ {я}}$ предполагая переход от набора слов ${ displaystyle { omega _ {1}, dots, omega _ {i}, dots, omega _ {k} }}$ к набору ${displaystyle {omega _{1},dots ,omega _{i}x,dots ,omega _{k}}}$.^[24][25]

This idea is further generalized to the case when ${ displaystyle T}$ is not given explicitly but instead is given by a prefix tree с ${ displaystyle Q}$ вершины. Mohri и другие. showed such an automaton would have at most ${displaystyle 2Q-2}$ and may be constructed in linear time from its size. At the same time, the number of transitions in such automaton may reach ${displaystyle O(Q|Sigma |)}$, for example for the set of words ${displaystyle T={sigma _{1},asigma _{1},a^{2}sigma _{1},dots ,a^{n}sigma _{1},a^{n}sigma _{2},dots ,a^{n}sigma _{k}}}$ over the alphabet ${displaystyle Sigma ={a,sigma _{1},dots ,sigma _{k}}}$ the total length of workds is equal to ${ extstyle O(n^{2}+nk)}$, the number of vertices in corresponding suffix trie is equal to ${ Displaystyle О (п + к)}$ and corresponding suffix automaton is formed of ${ Displaystyle О (п + к)}$ государства и ${displaystyle O(nk)}$ transitions. Algorithm suggested by Mohri mainly repeats the generic algorithm for building automaton of several strings but instead of growing words one by one, it traverses the trie in a breadth-first search order and append new characters as it meet them in the traversal, which guarantees amortized linear complexity.^[26]

Sliding window

Немного алгоритмы сжатия, Такие как LZ77 и RLE may benefit from storing suffix automaton or similar structure not for the whole string but for only last ${ displaystyle k}$ its characters while the string is updated. This is because compressing data is usually expressively large and using ${displaystyle O(n)}$ memory is undesirable. In 1985, Janet Blumer developed an algorithm to maintain a suffix automaton on a sliding window of size ${ displaystyle k}$ в ${displaystyle O(nk)}$ worst-case and ${displaystyle O(nlog k)}$ on average, assuming characters are distributed independently and равномерно. She also showed ${displaystyle O(nk)}$ complexity cannot be improved: if one considers words construed as a concatenation of several ${displaystyle (ab)^{m}c(ab)^{m}d}$ words, where ${displaystyle k=6m+2}$, then the number of states for the window of size ${ displaystyle k}$ would frequently change with jumps of order ${ displaystyle m}$, which renders even theoretical improvement of ${displaystyle O(nk)}$ for regular suffix automata impossible.^[27]

The same should be true for the suffix tree because its vertices correspond to states of the suffix automaton of the reversed string but this problem may be resolved by not explicitly storing every vertex corresponding to the suffix of the whole string, thus only storing vertices with at least two out-going edges. A variation of McCreight's suffix tree construction algorithm for this task was suggested in 1989 by Edward Fiala and Daniel Greene;^[28] several years later a similar result was obtained with the variation of Ukkonen's algorithm by Jesper Larsson.^[29][30] The existence of such an algorithm, for compacted suffix automaton that absorbs some properties of both suffix trees and suffix automata, was an open question for a long time until it was discovered by Martin Senft and Tomasz Dvorak in 2008, that it is impossible if the alphabet's size is at least two.^[31]

One way to overcome this obstacle is to allow window width to vary a bit while staying ${displaystyle O(k)}$. It may be achieved by an approximate algorithm suggested by Inenaga et al. in 2004. The window for which suffix automaton is built in this algorithm is not guaranteed to be of length ${ displaystyle k}$ but it is guaranteed to be at least ${ displaystyle k}$ and at most ${displaystyle 2k+1}$ while providing linear overall complexity of the algorithm.^[32]

Приложения

Suffix automaton of the string ${ displaystyle S}$ may be used to solve such problems as:^[33][34]

• Counting the number of distinct substrings of ${ displaystyle S}$ в ${displaystyle O(|S|)}$ on-line,
• Finding the longest substring of ${ displaystyle S}$ occurring at least twice in ${displaystyle O(|S|)}$,
• Finding the longest common substring of ${ displaystyle S}$ и ${ displaystyle T}$ в ${displaystyle O(|T|)}$,
• Counting the number of occurrences of ${ displaystyle T}$ в ${ displaystyle S}$ в ${displaystyle O(|T|)}$,
• Finding all occurrences of ${ displaystyle T}$ в ${ displaystyle S}$ в ${displaystyle O(|T|+k)}$, куда ${ displaystyle k}$ is the number of occurrences.

Здесь предполагается, что ${ displaystyle T}$ is given on the input after suffix automaton of ${ displaystyle S}$ is constructed.^[33]

Suffix automata are also used in data compression,^[35] music retrieval^[36][37] and matching on genome sequences.^[38]

Рекомендации

Библиография