Биголоморфизм - Biholomorphism
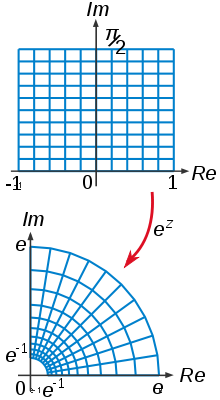
в математическая теория функций один или же более сложные переменные, а также в сложная алгебраическая геометрия, а биголоморфизм или же биголоморфная функция это биективный голоморфная функция чей обратный это также голоморфный.
Формальное определение
Формально биголоморфная функция это функция определено на открытое подмножество U из -мерное сложное пространство Cп со значениями в Cп который голоморфный и один к одному, так что его изображение это открытый набор в Cп и обратное это также голоморфный. В более общем смысле, U и V возможно комплексные многообразия. Как и в случае функций одной комплексной переменной, достаточным условием для того, чтобы голоморфное отображение было биголоморфным своему образу, является то, что отображение является инъективным, и в этом случае обратное также голоморфно (например, см. Ганнинг 1990, теорема I. 11).
Если существует биголоморфизм мы говорим, что U и V находятся биголоморфно эквивалентный или что они биголоморфный.
Теорема Римана об отображении и обобщения
Если каждый односвязный открытое множество, отличное от всей комплексной плоскости, биголоморфно единичный диск (это Теорема римана отображения ). В высших измерениях ситуация совсем иная. Например, откройте единичные шары и открыть блок полидиски не биголоморфно эквивалентны для На самом деле не существует даже правильный голоморфная функция от одного к другому.
Альтернативные определения
В случае карт ж : U → C определено на открытом подмножестве U комплексной плоскости C, некоторые авторы (например, Freitag 2009, определение IV.4.1) определяют конформная карта быть инъективным отображением с ненулевой производной, т. е. ж’(z) ≠ 0 для каждого z в U. Согласно этому определению, карта ж : U → C конформно тогда и только тогда, когда ж: U → ж(U) биголоморфна. Другие авторы (например, Conway 1978) определяют конформное отображение как отображение с ненулевой производной, не требуя, чтобы отображение было инъективным. Согласно этому более слабому определению конформности, конформное отображение не обязательно должно быть биголоморфным, даже если оно локально биголоморфно. Например, если ж: U → U определяется ж(z) = z2 с U = C- {0}, затем ж конформно на U, поскольку его производная ж’(z) = 2z 0, но он не биголоморфен, поскольку равен 2-1.
Рекомендации
- Джон Б. Конвей (1978). Функции одной комплексной переменной. Springer-Verlag. ISBN 3-540-90328-3.
- Джон П. Д'Анджело (1993). Несколько комплексных переменных и геометрия реальных гиперповерхностей. CRC Press. ISBN 0-8493-8272-6.
- Эберхард Фрайтаг и Рольф Бусам (2009). Комплексный анализ. Springer-Verlag. ISBN 978-3-540-93982-5.
- Роберт С. Ганнинг (1990). Введение в голоморфные функции многих переменных, Vol. II. Уодсворт. ISBN 0-534-13309-6.
- Стивен Г. Кранц (2002). Теория функций нескольких комплексных переменных. Американское математическое общество. ISBN 0-8218-2724-3.
Эта статья включает материал из биголоморфного эквивалента PlanetMath, который находится под лицензией Лицензия Creative Commons Attribution / Share-Alike.







