Соединение двенадцати пентаграммических призм - Википедия - Compound of twelve pentagrammic prisms
| Соединение двенадцати пентаграммических призм | |
|---|---|
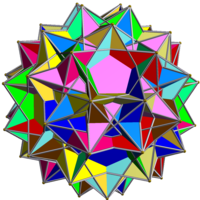 | |
| Тип | Равномерное соединение |
| Индекс | UC37 |
| Многогранники | 12 пентаграммические призмы |
| Лица | 24 пентаграммы, 60 квадраты |
| Края | 180 |
| Вершины | 60 |
| Группа симметрии | икосаэдр (ячас) |
| Подгруппа ограничиваясь одной составляющей | 5-кратный двугранный (D5) |
Этот однородное соединение многогранника симметричное расположение 12 пентаграммические призмы, попарно совмещенные с осями пятой вращательной симметрии додекаэдр.
Это результат объединения двух энантиоморфы из соединение шести пентаграмматических призм. При этом вершины двух энантиоморфов совпадают, в результате чего полное соединение имеет две пентаграммические призмы, инцидентные каждой из его вершин.
Связанные многогранники
Это соединение разделяет расположение вершин с четырьмя равномерные многогранники следующее:
 Ромбикосододекаэдр |  Малый додецикосододекаэдр |  Малый ромбидодекаэдр |
 Малый звездчатый усеченный додекаэдр |  Соединение шести пентаграммических призм |  Соединение двенадцати пентаграммических призм |
Рекомендации
- Скиллинг, Джон (1976), "Равномерные соединения однородных многогранников", Математические труды Кембриджского философского общества, 79 (03): 447–457, Дои:10.1017 / S0305004100052440, МИСТЕР 0397554.
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
