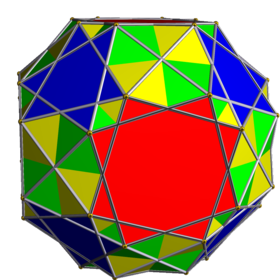
Соединение двух курносых кубиков - Compound of two snub cubes
| Соединение двух курносых кубиков | |
|---|---|
 | |
| Тип | Равномерное соединение |
| Показатель | UC68 |
| Символ Шлефли | βr {4,3} |
| Диаграмма Кокстера | |
| Многогранники | 2 курносые кубики |
| Лица | 16+48 треугольники 12 квадраты |
| Края | 120 |
| Вершины | 48 |
| Группа симметрии | восьмигранный (Очас) |
| Подгруппа ограничиваясь одной составляющей | хиральный восьмигранный (О) |
Эта однородное соединение многогранника это композиция из 2 энантиомеры из курносый куб. В качестве голоснуба он представлен Символ Шлефли βr {4,3} и Диаграмма Кокстера ![]()
![]()
![]()
![]()
![]() .
.
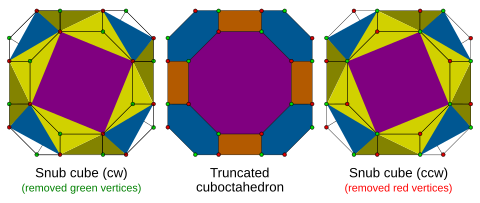
В расположение вершин этого соединения разделяет выпуклая неоднородная усеченный кубооктаэдр, имеющий прямоугольные грани, рядом с неправильными шестиугольники и восьмиугольники, каждая из которых чередуется с двумя длинами кромок.
Вместе со своей выпуклой оболочкой он представляет собой плоскостную проекцию неоднородной курносая кубическая антипризма.
Декартовы координаты
Декартовы координаты для вершины все перестановки из
- (±1, ±ξ, ±1/ξ)
где ξ это реальное решение
что можно написать
или примерно 0,543689. ξ - обратная величина постоянная трибоначчи.
Точно так же постоянная трибоначчи, т, как и курносый куб, может вычислить координаты как:
- (±1, ±т, ±1/т)
Усеченный кубооктаэдр
Это соединение можно рассматривать как объединение двух хиральных чередований усеченный кубооктаэдр:
Смотрите также
использованная литература
- Скиллинг, Джон (1976), "Равномерные соединения однородных многогранников", Математические труды Кембриджского философского общества, 79: 447–457, Дои:10.1017 / S0305004100052440, Г-Н 0397554.
| Эта многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |


![xi = {frac {1} {3}} left ({sqrt [{3}] {17 + 3 {sqrt {33}}}} - {sqrt [{3}] {- 17 + 3 {sqrt {33}} }}} - 1 ночь)](https://wikimedia.org/api/rest_v1/media/math/render/svg/737fbacde6c58fa15561c938c9671e63403908ee)