Элементарный поток - Википедия - Elementary flow
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
Элементарный поток представляет собой набор основных потоков, из которых можно построить более сложные потоки, суперпозиция. Некоторые из потоков отражают конкретные случаи и ограничения, такие как несжимаемый, безвихревый или оба, как в случае Потенциальный поток.[1]
Двумерный равномерный поток
Учитывая равномерную скорость жидкости в любой точке пространства:
Этот поток несжимаемый, потому что скорость постоянна, первые производные компонентов скорости равны нулю, а полная дивергенция равна нулю:
Учитывая обращение всегда равен нулю, поток также является безвихревым, это можно вывести из Теорема циркуляции Кельвина и из явного вычисления Завихренность:
Этот несжимаемый и двумерный поток построен из функция потока
откуда
И в цилиндрических координатах:
откуда
Как обычно, функция потока определяется до постоянного значения, которое здесь мы принимаем за ноль. Мы также можем подтвердить, что поток является безвихревым от
Потенциальная функция, будучи безвихревой, вместо этого:
и поэтому
Источник двухмерной линии
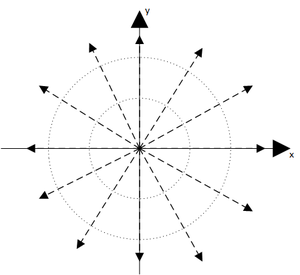
Случай вертикальной линии, испускающей с фиксированной скоростью постоянное количество жидкости Q на единицу длины, является линейным источником. Задача имеет цилиндрическую симметрию и может рассматриваться в двух измерениях на ортогональной плоскости.
Линейные источники и линейные стоки (ниже) являются важными элементарными потоками, поскольку они играют роль монополя (ов) для несжимаемых жидкостей (которые также можно рассматривать как примеры соленоидные поля т.е. поля без расходимости). Общие схемы потока также могут быть декомпозированы с точки зрения мультипольные разложения, так же, как и для электрический и магнитный поля, в которых монополь по существу является первым нетривиальным (например, постоянным) членом разложения.
Этот режим течения также является как безвихревым, так и несжимаемым.
Для этого характерна цилиндрическая симметрия:
Где общий исходящий поток постоянен
Следовательно,
Это получено из функции потока
или от потенциальной функции
Двухмерная раковина
Случай, когда вертикальная линия поглощает с фиксированной скоростью постоянное количество жидкости Q на единицу длины, является линейным стоком. Все происходит так же, как и в случае линейного источника - части с отрицательным знаком.
Это получено из функции потока
или от потенциальной функции
Учитывая, что эти два результата совпадают в части от знака минус, мы можем прозрачно рассматривать как линейные источники, так и линейные поглотители с одинаковыми потоками и потенциальными функциями, позволяющими Q принимать как положительные, так и отрицательные значения и поглощать знак минус в определении Q .
Двухмерный дублетный или дипольный линейный источник
Если мы рассмотрим линейный источник и линейный сток на расстоянии d, мы можем повторно использовать приведенные выше результаты, и функция потока будет
Последнее приближение к первому порядку по d.
Данный
Это остается
Тогда скорость
И вместо этого потенциал
Двумерная вихревая линия

Это случай вихревой нити, вращающейся с постоянной скоростью, имеется цилиндрическая симметрия, и задача может быть решена в ортогональной плоскости.
Двойные по отношению к рассмотренному выше случаю линейных источников, вихревые линии играют роль монополей для безвихревые потоки.
Также в этом случае поток также является безвихревый и несжимаемый и поэтому случай Потенциальный поток.
Для этого характерна цилиндрическая симметрия:
Где общая циркуляция постоянна для каждой замкнутой линии вокруг центрального вихря.
и равен нулю для любой линии, не включая вихрь.
Следовательно,
Это получено из функции потока
или от потенциальной функции
Что двойственно предыдущему случаю линейного источника
Типовой двумерный потенциальный поток
Для несжимаемого двумерного потока, который также является безвихревым, имеем:
Которая находится в цилиндрических координатах [2]
Ищем решение с разделенными переменными:
который дает
Учитывая, что левая часть зависит только от r, а правая часть зависит только от:, две части должны быть равны константе, не зависящей от r и . Константа должна быть положительной.[требуется разъяснение ].Следовательно,
Решение второго уравнения представляет собой линейную комбинацию и Чтобы иметь однозначную скорость (а также однозначную функцию тока), m должно быть положительным целым числом.
поэтому наиболее общее решение дается
Потенциал вместо этого дается
Рекомендации
- Фитцпатрик, Ричард (2017), Теоретическая гидродинамика, IOP science, ISBN 978-0-7503-1554-8
- Фабер, Т. (1995), Гидродинамика для физиков, Издательство Кембриджского университета, ISBN 9780511806735
- Специфический
- ^ Оливер, Дэвид (2013-03-14). Косматый конь физики: математическая красота в физическом мире. Springer Science & Business Media. ISBN 978-1-4757-4347-0.
- ^ Оператор Лапласа
дальнейшее чтение
- Бэтчелор, Г. (1973), Введение в гидродинамику, Издательство Кембриджского университета, ISBN 978-0-521-09817-5
- Шансон, Х. (2009), Прикладная гидродинамика: введение в идеальные и реальные потоки жидкости, CRC Press, Taylor & Francis Group, Лейден, Нидерланды, 478 страниц, ISBN 978-0-415-49271-3
- Лэмб, Х. (1994) [1932], Гидродинамика (6-е изд.), Cambridge University Press, ISBN 978-0-521-45868-9
- Милн-Томсон, Л. (1996) [1968], Теоретическая гидродинамика (5-е изд.), Дувр, ISBN 978-0-486-68970-8
внешняя ссылка
- Ричард Фицпатрик Техасский университет, Остин (2017). «Механика жидкости». Техасский университет, Остин. Получено 2018-02-07.
- (c) Aerospace, Mechanical & Mechatronic Engg. 2005 г. Сиднейский университет (2005). «Элементы потенциального потока». Сиднейский университет. Получено 2019-04-19.


























![{ displaystyle mathbf {d} = d [соз theta _ {0} mathbf {e} _ {x} + sin theta _ {0} mathbf {e} _ {y}] = d [cos ( theta - theta _ {0}) mathbf {e} _ {r} + sin ( theta - theta _ {0}) mathbf {e} _ { theta}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b63a01c7db89249cbcca94f720d6411e844b7bde)

















![{ displaystyle psi = alpha _ {0} + beta _ {0} ln r + sum _ {m mathop {>} 0} {( alpha _ {m} r ^ {m} + beta _ {m} r ^ {- m}) sin {[m ( theta - theta _ {m})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc1c0aede6c898d4fd77e7edc649b0ffd22173ba)
![{ displaystyle phi = alpha _ {0} - beta _ {0} theta + sum _ {m mathop {>} 0} {( alpha _ {m} r ^ {m} - beta _ {m} r ^ {- m}) cos {[m ( theta - theta _ {m})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ae11d9c0fa83d2856902127f9cd620c057980ee)