Формула длины крючка - Википедия - Hook length formula

В комбинаторная математика, то формула длины крючка это формула для количества стандартные картины Юнга чья форма дана Диаграмма Юнга.Он имеет приложения в различных области Такие как теория представлений, вероятность, и анализ алгоритма; например, проблема самые длинные возрастающие подпоследовательности. Связанная формула подсчитывает количество полустандартных таблиц Юнга, которые являются специализацией Полином Шура.

Определения и заявление

Позволять ${ displaystyle lambda = ( lambda _ {1} geq cdots geq lambda _ {k})}$ быть раздел из ${ Displaystyle п = лямбда _ {1} + cdots + лямбда _ {к}}$.Принято толковать ${ displaystyle lambda}$ графически как Диаграмма Юнга, а именно выровненный по левому краю массив квадратных ячеек с ${ displaystyle k}$ ряды длин ${ displaystyle lambda _ {1}, ldots, lambda _ {k}}$.A (стандарт) Молодая картина формы ${ displaystyle lambda}$ это наполнение ${ displaystyle n}$ ячейки диаграммы Юнга со всеми целыми числами ${ Displaystyle {1, ldots, п }}$, без повторения, так что каждая строка и каждый столбец образуют возрастающие последовательности. ${ displaystyle (я, j)}$, в ${ displaystyle i}$й ряд и ${ displaystyle j}$-й столбец крюк ${ displaystyle H _ { lambda} (я, j)}$ это набор ячеек ${ Displaystyle (а, б)}$ такой, что ${ Displaystyle а = я}$ и ${ displaystyle b geq j}$ или же ${ displaystyle a geq i}$ и ${ displaystyle b = j}$.Длина крючка. ${ displaystyle h _ { lambda} (я, j)}$ количество ячеек в ${ displaystyle H _ { lambda} (я, j)}$.

Формула длины крючка выражает количество стандартных таблиц формы Юнга. ${ displaystyle lambda}$, обозначаемый ${ displaystyle f ^ { lambda}}$ или же ${ displaystyle d _ { lambda}}$, так как

${ displaystyle f ^ { lambda} = { frac {n!} { prod h _ { lambda} (i, j)}},}$

где продукт по всем ячейкам ${ displaystyle (я, j)}$ диаграммы Юнга.

Примеры

Таблица с указанием длины крючка каждой ячейки на диаграмме Юнга
${ Displaystyle (4,3,1,1)}$

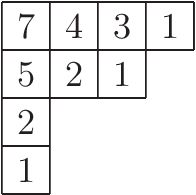
На рисунке справа показаны длины крючков для ячеек в Диаграмма Юнга ${ displaystyle lambda = (4,3,1,1)}$, соответствующий разбиению 9 = 4 + 3 + 1 + 1. Формула длины крюка дает количество стандартных таблиц Юнга как:

${ Displaystyle е ^ { лямбда} = { frac {9!} {7 cdot 5 cdot 4 cdot 3 cdot 2 cdot 2 cdot 1 cdot 1 cdot 1}} = 216.}$

А Каталонский номер ${ displaystyle C_ {n}}$считает пути Дика с ${ displaystyle n}$ шаги вверх (U) с вкраплениями ${ displaystyle n}$ шаги вниз (D), так что на каждом шаге никогда не бывает больше D, чем U. Они находятся в противоречии с таблицами форм Юнга. ${ Displaystyle лямбда = (п, п)}$: путь Дика соответствует таблице, в первой строке которой перечислены позиции U-ступеней, а во второй строке - позиции D-ступеней. Например, UUDDUD соответствуют таблицам со строками 125 и 346.

Это показывает, что ${ Displaystyle C_ {п} = е ^ {(п, п)}}$, поэтому формула крючка специализируется на хорошо известной формуле продукта

${ Displaystyle C_ {n} = { frac {(2n)!} {(n {+} 1) (n) cdots (3) (2) (n) (n {-} 1) cdots (2) (1)}} = { frac {(2n)!} {(N {+} 1)! N!}} = { Frac {1} {n {+} 1}} { binom {2n} {n}}.}$

История

Есть и другие формулы для ${ displaystyle f ^ { lambda}}$, но формула длины крючка особенно проста и элегантна. Менее удобная формула, выражающая ${ displaystyle f ^ { lambda}}$ с точки зрения детерминант был выведен независимо Фробениус и Молодой в 1900 и 1902 годах соответственно с использованием алгебраических методов.^[1][2]MacMahon нашел альтернативное доказательство формулы Юнга – Фробениуса в 1916 г., используя разностные методы.^[3]

Сама формула длины крючка была открыта в 1953 году Фреймом. Робинсон, и Тралл как улучшение формулы Юнга – Фробениуса. Саган^[4] описывает открытие следующим образом.

Однажды в четверг мая 1953 года Робинсон посетил Фрейма в Университете штата Мичиган. Обсуждая работу Стаала (ученика Робинсона), Фрейм пришел к выводу о формуле крючка. Сначала Робинсон не мог поверить, что такая простая формула существует, но, попробовав несколько примеров, он убедился, и вместе они подтвердили идентичность. В субботу они отправились в Мичиганский университет, где Фрейм представил свой новый результат после лекции Робинсона. Это удивило Тралла, который был в зале, потому что он только что доказал тот же результат в тот же день!

Несмотря на простоту формулы длины крючка, доказательство Фрейма – Робинсона – Тралла не очень информативно и не дает никакого интуитивного представления о роли крючков. Поиск краткого, интуитивно понятного объяснения, подходящего к такому простому результату, привел к появлению множества альтернативных доказательств.^[5]Хиллман и Грассл дали первое доказательство, проливающее свет на роль крючков, в 1976 году, доказав частный случай Стэнли формула содержания крючка, которая, как известно, подразумевает формулу длины крючка.^[6]Грин, Nijenhuis, и Уилф нашел вероятностное доказательство, используя прогулку на крючке, в которой длина крюка появляется естественным образом в 1979 году.^[7]Реммель адаптировал исходное доказательство Фрейма – Робинсона – Тралла в первое биективное доказательство для формулы длины крюка в 1982 году.^[8]Прямое биективное доказательство было впервые открыто Францблау и Zeilberger в 1982 г.^[9]Zeilberger также преобразовал доказательство прогулки по крюку Грина – Нийенхейса – Уилфа в биективное доказательство в 1984 году.^[10] Более простая прямая биекция была объявлена Пак и Стояновского в 1992 г., а его полное доказательство было представлено парой и Новелли в 1997 г.^[11][12][13]

Между тем, формула длины крючка была обобщена несколькими способами. М. Тралл нашел аналог формулы длины крючка для смещенных таблиц Юнга в 1952 году.^[14] Саган предоставил доказательство смещения крюка для формулы длины крюка для смещенных таблиц Юнга в 1980 году.^[15] Саган и Йе доказали формулу длины крюка для бинарных деревьев с помощью прогулки на крючке в 1989 году.^[16] Проктор дал некоторое обобщение (см. Ниже).

Вероятностное доказательство

Эвристический аргумент Кнута

Формулу длины крюка можно интуитивно понять, используя следующий эвристический, но неверный аргумент, предложенный Д. Э. Кнут.^[17]Учитывая, что каждый элемент таблицы является наименьшим в своем крючке и заполняет форму таблицы случайным образом, вероятность того, что ячейка ${ displaystyle (я, j)}$ будет содержать минимальный элемент соответствующего крючка, обратно пропорциональный длине крючка. Умножая эти вероятности на все ${ displaystyle i}$ и ${ displaystyle j}$ дает формулу. Этот аргумент ошибочен, поскольку события не являются независимыми.

Однако аргумент Кнута верен для перечисления меток на деревьях, удовлетворяющих свойствам монотонности, аналогичным свойствам таблицы Юнга. В этом случае рассматриваемые события «крючка» фактически являются независимыми событиями.

Вероятностное доказательство с использованием крюковой прогулки

Это вероятностное доказательство, найденное К. Грин, А. Нийенхейс, и Х. С. Вильф в 1979 г.^[18] Определять

${ displaystyle e _ { lambda} = { frac {n!} { prod _ {(i, j) in Y ( lambda)} h _ { lambda} (i, j)}}.}$

Мы хотим показать, что ${ displaystyle f ^ { lambda} = e _ { lambda}}$. Первый,

${ displaystyle f ^ { lambda} = sum _ { mu uparrow lambda} f ^ { mu},}$

Углы диаграммы Юнга (5,3,2,1,1)

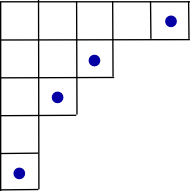
где сумма пробегает все диаграммы Юнга ${ displaystyle mu}$ получен из ${ displaystyle lambda}$ удалив одну угловую ячейку. (Максимальный вход таблицы Юнга формы ${ displaystyle lambda}$ происходит в одной из его угловых ячеек, поэтому удаление дает таблицы Юнга формы ${ displaystyle mu}$.)

Мы определяем ${ displaystyle f ^ { emptyset} = 1}$и ${ Displaystyle е _ { emptyset} = 1}$, поэтому достаточно показать такое же повторение

${ displaystyle e _ { lambda} = sum _ { mu uparrow lambda} e _ { mu},}$

что означало бы ${ displaystyle f ^ { lambda} = e _ { lambda}}$ по индукции. Приведенную выше сумму можно рассматривать как сумму вероятностей, записав ее как

${ displaystyle sum _ { mu uparrow lambda} { frac {e _ { mu}} {e _ { lambda}}} = 1.}$

Следовательно, нам нужно показать, что числа ${ displaystyle { frac {е _ { mu}} {е _ { lambda}}}}$ определить вероятностную меру на множестве диаграмм Юнга ${ displaystyle mu}$ с ${ displaystyle mu uparrow lambda}$. Это делается конструктивным образом путем определения случайного блуждания, называемого прогулка на крючке, на ячейках диаграммы Юнга ${ displaystyle lambda}$, который в конечном итоге выбирает одну из угловых ячеек ${ displaystyle lambda}$ (которые находятся в взаимно однозначном соответствии с диаграммами ${ displaystyle mu}$ для которого ${ displaystyle mu uparrow lambda}$). Ход крюка определяется следующими правилами.

1. Выбрать ячейку равномерно случайным образом из ${ displaystyle | lambda |}$ клетки. Начните оттуда случайное блуждание.
2. Преемник текущей ячейки ${ displaystyle (я, j)}$ выбирается равномерно случайным образом из крючка ${ Displaystyle Н _ { лямбда} (я, j) ​​ setminus {(я, j) ​​}}$.
3. Продолжайте, пока не дойдете до угловой ячейки ${ displaystyle { textbf {c}}}$.

Предложение: Для данной угловой ячейки ${ Displaystyle (а, б)}$ из ${ displaystyle lambda}$, у нас есть

${ displaystyle mathbb {P} left ({ textbf {c}} = (a, b) right) = { frac {e _ { mu}} {e _ { lambda}}},}$

куда ${ displaystyle mu = lambda setminus {(a, b) }}$.

Учитывая это, суммируя по всем угловым ячейкам ${ Displaystyle (а, б)}$ дает ${ displaystyle sum _ { mu uparrow lambda} { frac {е _ { mu}} {е _ { lambda}}} = 1}$ как заявлено.

Связь с представлениями симметрической группы

Формула длины крючка имеет большое значение в теория представлений симметрической группы ${ displaystyle S_ {n}}$, где число ${ displaystyle f ^ { lambda}}$ как известно, равна размерности комплексного неприводимого представления ${ displaystyle V _ { lambda}}$ связано с ${ displaystyle lambda}$.

Подробное обсуждение

Комплексные неприводимые представления ${ displaystyle V _ { lambda}}$ симметрической группы индексируются разбиениями ${ displaystyle lambda}$ из ${ displaystyle n}$ (видеть Модуль Specht ). Их характеры связаны с теорией симметричных функций через внутреннее произведение Холла:

${ displaystyle chi ^ { lambda} (w) = langle s _ { lambda}, p _ { tau (w)} rangle,}$

куда ${ displaystyle s _ { lambda}}$ это Функция Шура связано с ${ displaystyle lambda}$ и ${ Displaystyle р _ { тау (ш)}}$ является степенной симметричной функцией разбиения ${ Displaystyle тау (ш)}$ связанный с циклической декомпозицией ${ displaystyle w}$. Например, если ${ Displaystyle ш = (154) (238) (6) (79)}$ тогда ${ Displaystyle тау (ш) = (3,3,2,1)}$.

Поскольку тождественная перестановка ${ displaystyle e}$ имеет форму ${ Displaystyle е = (1) (2) cdots (п)}$ в обозначении цикла, ${ Displaystyle тау (е) = (1, ldots, 1) = 1 ^ {(п)}}$, формула говорит

${ displaystyle f ^ { lambda} , = , dim V _ { lambda} , = , chi ^ { lambda} (e) , = , langle s _ { lambda}, p_ {1 ^ {(n)}} rangle}$

Разложение функций Шура по мономиальным симметрическим функциям использует Костка номера:

${ displaystyle s _ { lambda} = sum _ { mu} K _ { lambda mu} m _ { mu},}$

Затем внутренний продукт с ${ displaystyle p_ {1 ^ {(n)}} = h_ {1 ^ {(n)}}}$ является ${ Displaystyle К _ { лямбда 1 ^ {(п)}}}$, потому что ${ displaystyle langle m _ { mu}, h _ { nu} rangle = delta _ { mu nu}}$. Обратите внимание, что ${ Displaystyle К _ { лямбда 1 ^ {(п)}}}$ равно ${ displaystyle f ^ { lambda} = dim V _ { lambda}}$, так что ${ displaystyle textstyle sum _ { lambda vdash n} left (f ^ { lambda} right) ^ {2} = n!}$ от рассмотрения регулярное представительство из ${ displaystyle S_ {n}}$, или комбинаторно из Переписка Робинсона – Шенстеда – Кнута.

Расчет также показывает, что:

${ displaystyle (x_ {1} + x_ {2} + cdots + x_ {k}) ^ {n} = sum _ { lambda vdash n} s _ { lambda} f ^ { lambda}.}$

Это расширение ${ displaystyle p_ {1 ^ {(n)}}}$ в терминах функций Шура с использованием коэффициентов, заданных внутренним произведением, поскольку ${ displaystyle langle s _ { mu}, s _ { nu} rangle = delta _ { mu nu}}$Приведенное выше равенство можно доказать, также проверив коэффициенты каждого одночлена с обеих сторон и используя Переписка Робинсона – Шенстеда – Кнута или, более концептуально, глядя на разложение ${ displaystyle V ^ { otimes n}}$ несводимым ${ Displaystyle GL (V)}$ модули и взятие персонажей. Видеть Двойственность Шура – ​​Вейля.

Доказательство формулы крюка с использованием формулы Фробениуса^[19]

По приведенным выше соображениям

${ displaystyle p_ {1 ^ {(n)}} = sum _ { lambda vdash n} s _ { lambda} f ^ { lambda}}$

так что

${ Displaystyle Delta (x) p_ {1 ^ {(n)}} = sum _ { lambda vdash n} Delta (x) s _ { lambda} f ^ { lambda}}$

куда ${ displaystyle Delta (x) = prod _ {я$ это Определитель Вандермонда.

Для раздела ${ displaystyle lambda = ( lambda _ {1} geq cdots geq lambda _ {k})}$, определять ${ displaystyle l_ {i} = lambda _ {i} + k-i}$ за ${ Displaystyle я = 1, ldots, к}$. Для дальнейшего нам понадобится как минимум столько же переменных, сколько строк в разделе, поэтому с этого момента мы работаем с ${ displaystyle n}$ переменные ${ displaystyle x_ {1}, cdots, x_ {n}}$.

Каждый термин ${ displaystyle Delta (x) s _ { lambda}}$ равно

${ displaystyle a _ {( lambda _ {1} + k-1, lambda _ {2} + k-2, dots, lambda _ {k})} (x_ {1}, x_ {2}, dots, x_ {k}) = det ! left [{ begin {matrix} x_ {1} ^ {l_ {1}} & x_ {2} ^ {l_ {1}} & dots & x_ {k} ^ {l_ {1}} x_ {1} ^ {l_ {2}} & x_ {2} ^ {l_ {2}} & dots & x_ {k} ^ {l_ {2}} vdots & vdots & ddots & vdots x_ {1} ^ {l_ {k}} & x_ {2} ^ {l_ {k}} & dots & x_ {k} ^ {l_ {k}} конец {матрица}} right]}$

(Видеть Функция Шура.) Поскольку вектор ${ displaystyle (l_ {1}, ldots, l_ {k})}$ отличается для каждого раздела, это означает, что коэффициент ${ Displaystyle x_ {1} ^ {l_ {1}} cdots x_ {k} ^ {l_ {k}}}$ в ${ displaystyle Delta (x) p_ {1 ^ {(n)}}}$, обозначенный ${ displaystyle left [ Delta (x) p_ {1 ^ {(n)}} right] _ {l_ {1}, cdots, l_ {k}}}$, равно ${ displaystyle f ^ { lambda}}$. Это известно как Формула характера Фробениуса, что дает одно из самых ранних доказательств.^[20]

Осталось только упростить этот коэффициент. Умножение

${ displaystyle Delta (x) = sum _ {w in S_ {n}} operatorname {sgn} (w) x_ {1} ^ {w (1) -1} x_ {2} ^ { ш (2) -1} cdots x_ {k} ^ {w (k) -1}}$

и

${ displaystyle p_ {1 ^ {(n)}} = (x_ {1} + x_ {2} + cdots + x_ {k}) ^ {n} = sum { frac {n! } {d_ {1}! d_ {2}! cdots d_ {k}!}} x_ {1} ^ {d_ {1}} x_ {2} ^ {d_ {2}} cdots x_ {k} ^ {d_ {k}}}$

заключаем, что наш коэффициент как

${ displaystyle sum _ {w in S_ {n}} operatorname {sgn} (w) { frac {n!} {(l_ {1} -w (1) +1)! cdots (l_ { k} -w (k) +1)!}}}$

который можно записать как

${ displaystyle { frac {n!} {l_ {1}! l_ {2}! cdots l_ {k}!}} sum _ {w in S_ {n}} operatorname {sgn} (w) left [(l_ {1}) (l_ {1} -1) cdots (l_ {1} -w (1) +2) right] left [(l_ {2}) (l_ {2} - 1) cdots (l_ {2} -w (2) +2) right] left [(l_ {k}) (l_ {k} -1) cdots (l_ {k} -w (k) + 2) right]}$

Последняя сумма равна определителю

${ displaystyle det left [{ begin {matrix} 1 & l_ {1} & l_ {1} (l_ {1} -1) & dots & prod _ {i = 0} ^ {k-2} (l_ {1} -i) 1 & l_ {2} & l_ {2} (l_ {2} -1) & dots & prod _ {i = 0} ^ {k-2} (l_ {2} -i) vdots & vdots & vdots & ddots & vdots 1 & l_ {k} & l_ {k} (l_ {k} -1) & dots & prod _ {i = 0} ^ {k- 2} (l_ {k} -i) end {matrix}} right]}$

который столбец сводится к Определитель Вандермонда, и мы получаем формулу

${ displaystyle f ^ { lambda} = { frac {n!} {l_ {1}! l_ {2}! cdots l_ {k}!}} prod _ {i$

Обратите внимание, что ${ displaystyle l_ {i}}$ - длина крючка первого прямоугольника в каждой строке диаграммы Юнга, и это выражение легко преобразуется в желаемый вид ${ displaystyle { frac {n!} { prod h _ { lambda} (i, j)}}}$: один показывает ${ displaystyle textstyle l_ {i}! = prod _ {j> i} (l_ {i} -l_ {j}) cdot prod _ {j leq lambda _ {i}} h_ { lambda} (i, j)}$, где последний продукт пробегает ${ displaystyle i}$-я строка диаграммы Юнга.

Связь с самыми длинными возрастающими подпоследовательностями

Формула длины крюка также имеет важные приложения для анализа самые длинные возрастающие подпоследовательности в случайных перестановках. Если ${ displaystyle sigma _ {n}}$ обозначает равномерно случайную перестановку порядка ${ displaystyle n}$, ${ Displaystyle L ( sigma _ {п})}$ обозначает максимальную длину возрастающей подпоследовательности ${ displaystyle sigma _ {n}}$, и ${ displaystyle ell _ {n}}$ обозначает ожидаемое (среднее) значение ${ Displaystyle L ( sigma _ {п})}$, Анатолий Вершик и Сергей Керов ^[21] и независимо Бенджамин Ф. Логан и Лоуренс А. Шепп^[22] показал, что когда ${ displaystyle n}$ большой, ${ displaystyle ell _ {n}}$ примерно равно ${ displaystyle 2 { sqrt {n}}}$. Это отвечает на вопрос, первоначально заданный Станислав Улам. Доказательство основано на переводе вопроса через Переписка Робинсона – Шенстеда к задаче о предельной форме случайной таблицы Юнга, выбранной согласно Планшерель мера. Поскольку в определение меры Планшереля входит величина ${ displaystyle f ^ { lambda}}$формула длины крюка может затем использоваться для выполнения асимптотического анализа предельной формы и, таким образом, также отвечать на исходный вопрос.

Идеи Вершика – Керова и Логана – Шеппа позже были уточнены Джинхо Байком, Перси Дейфтом и Куртом Йоханссоном, которые смогли добиться гораздо более точного анализа предельного поведения максимальной увеличивающейся длины подпоследовательности, доказав важный теперь известный результат как теорема Байка – Дейфта – Йоханссона. Их анализ снова решительно использует тот факт, что ${ displaystyle f ^ { lambda}}$ имеет ряд хороших формул, хотя вместо формулы длины крюка используется одно из определяющих выражений.

Связанные формулы

Формула числа таблиц фигуры Юнга ${ displaystyle lambda}$ был первоначально получен из Формула определителя Фробениуса в связи с теорией представлений:^[23]

${ displaystyle f ( lambda _ {1}, ldots, lambda _ {k}) = { frac {n! , Delta ( lambda _ {k}, lambda _ {k-1 } +1, ldots, lambda _ {1} + k-1)} { lambda _ {k}! ( Lambda _ {k-1} +1)! Cdots ( lambda _ {1} + к-1)!}}.}$

Длину крючков также можно использовать для представления продукта производящей функции для количества обратных плоских секций заданной формы.^[24] Если λ является разбиением некоторого целого числа п, обратное плоское разбиение п с формой λ получается заполнением полей диаграммы Юнга неотрицательными целыми числами, так что элементы добавляются к п и не убывают вдоль каждой строки и вниз по каждому столбцу. Длина крючка ${ displaystyle h_ {1}, dots, h_ {p}}$ можно определить как с таблицами Юнга. Если π_п обозначает количество обратных плоскостных разбиений п с формой λ, то производящую функцию можно записать как

${ displaystyle sum _ {n = 0} ^ { infty} pi _ {n} x ^ {n} = prod _ {k = 1} ^ {p} (1-x ^ {h_ {k}) }) ^ {- 1}}$

Стэнли открыл другую формулу для той же производящей функции.^[25] В общем, если ${ displaystyle A}$ есть ли какой-нибудь посет с ${ displaystyle n}$ элементов, производящая функция для обратного ${ displaystyle A}$-partitions это

${ Displaystyle { гидроразрыва {P (x)} {(1-x) (1-x ^ {2}) cdots (1-x ^ {n})}}}$

куда ${ Displaystyle P (x)}$ - многочлен такой, что ${ Displaystyle P (1)}$ это количество линейные расширения из ${ displaystyle A}$.

В случае перегородки ${ displaystyle lambda}$, мы рассматриваем ч.у.м. в его ячейках, заданных соотношением

${ displaystyle (я, j) ​​ leq (i ', j') iff i leq i ' qquad { textrm {and}} qquad j leq j'}$.

Таким образом, линейное расширение - это просто стандартная таблица Юнга, т.е. ${ Displaystyle P (1) = е ^ { лямбда}}$

Доказательство формулы крючка с использованием формулы Стэнли

Комбинируя две формулы для производящих функций, мы имеем

${ Displaystyle { гидроразрыва {P (x)} {(1-x) (1-x ^ {2}) cdots (1-x ^ {n})}} = prod _ {(i, j) in lambda} (1-x ^ {h _ {(i, j)}}) ^ {- 1}}$

Обе стороны сходятся внутри диска радиуса один, и следующее выражение имеет смысл для ${ Displaystyle | х | <1}$

${ Displaystyle P (x) = { гидроразрыва { prod _ {k = 1} ^ {n} (1-x ^ {k})} { prod _ {(i, j) in lambda} ( 1-x ^ {h _ {(i, j)}})}}.}$

Было бы жестоко вставлять 1, но правая часть - это непрерывная функция внутри единичного круга, а многочлен непрерывен всюду, поэтому, по крайней мере, мы можем сказать

${ Displaystyle P (1) = lim _ {x to 1} { frac { prod _ {k = 1} ^ {n} (1-x ^ {k})} { prod _ {(i , j) in lambda} (1-x ^ {h _ {(i, j)}})}}.}$

Применение Правило L'Hôpital ${ displaystyle n}$ раз дает формулу длины крючка

${ displaystyle P (1) = { frac {n!} { prod _ {(i, j) in lambda} h _ {(i, j)}}}.}.$

Формула длины крючка полустандартных таблиц

В Полином Шура ${ displaystyle s _ { lambda} (x_ {1}, ldots, x_ {k})}$ - производящая функция полустандартного Молодые картины с формой ${ displaystyle lambda}$ и записи в ${ Displaystyle {1, ldots, к }}$. Специализируясь на этом ${ displaystyle x_ {i} = 1}$ дает количество полустандартных таблиц, которые можно записать в единицах длины крючка:

${ displaystyle s _ { lambda} (1, ldots, 1) = prod _ {(i, j) in mathrm {Y} ( lambda)} { frac {k-i + j} {h _ { lambda} (i, j)}}.}$

Диаграмма Юнга ${ displaystyle lambda}$ соответствует для неприводимое представление из специальная линейная группа ${ Displaystyle mathrm {SL} _ {к} ( mathbb {C})}$, а многочлен Шура также является характером диагональной матрицы ${ Displaystyle mathrm {diag} (x_ {1}, ldots, x_ {k})}$ действуя по этому представлению. Таким образом, указанная выше специализация является размерностью неприводимого представления, а формула является альтернативой более общей Формула размерности Вейля.

Мы можем уточнить это, взяв основную специализацию функции Шура в переменных ${ Displaystyle 1, т, т ^ {2} !, т ^ {3} !, ldots}$ :

${ displaystyle s _ { lambda} (1, t, t ^ {2}, ldots) = { frac {t ^ {n left ( lambda right)}} { prod _ {(i , j) in Y ( lambda)} (1-t ^ {h _ { lambda} (i, j)})}},}$

куда ${ Displaystyle п ( лямбда) = сумма _ {я} (я {-} 1) лямбда _ {я} = сумма _ {я} { tbinom { лямбда _ {я} '} {2} }}$ для сопряженного разбиения ${ displaystyle lambda '}$.

Формула перекоса

Существует обобщение этой формулы для перекосов,^[26]

${ displaystyle s _ { lambda / mu} (1, t, t ^ {2}, cdots) = sum _ {S in E ( lambda / mu)} prod _ {(i, j ) in lambda setminus S} { frac {t ^ { lambda _ {j} '- i}} {1-t ^ {h (i, j)}}}}$

где сумма берется возбужденные диаграммы формы ${ displaystyle lambda}$ и коробки распределены согласно ${ displaystyle mu}$.

Обобщение на d-полные посеты

Диаграммы Юнга можно рассматривать как конечные идеалы порядка в позе ${ Displaystyle mathbb {N} times mathbb {N}}$, а стандартные таблицы Юнга - их линейные расширения. Роберт Проктор дал обобщение формулы длины крюка для подсчета линейных расширений более широкого класса множеств, обобщающих как деревья, так и косые диаграммы.^[27][28]

Рекомендации

внешняя ссылка

• Удивительная математика самых длинных возрастающих подпоследовательностей пользователя Dan Romik. Содержит обсуждение формулы длины крюка и нескольких ее вариантов с приложениями к математике самых длинных возрастающих подпоследовательностей.