Минимальная масса - Википедия - Minimum mass

Оставили: Изображение звезды, вращающейся вокруг планеты. Все движение звезды происходит в пределах прямой видимости зрителя; Доплеровская спектроскопия даст истинное значение массы планеты.
Правильно: В этом случае звезда не движется по линии прямой видимости зрителя, и метод доплеровской спектроскопии вообще не обнаружит планету.

В астрономия, минимальная масса вычисляется нижняя граница масса наблюдаемых объектов, таких как планеты, звезды и двоичные системы,[1] туманности,[2] и черные дыры.

Минимальная масса - это широко цитируемая статистика для внесолнечные планеты обнаружен метод лучевых скоростей или доплеровской спектроскопии, и определяется с помощью бинарная функция масс. Этот метод обнаруживает планеты, измеряя изменения в движении звезд в Поле зрения так что настоящий орбитальные наклонения а истинные массы планет обычно неизвестны.[3] Это результат Грех я вырождение.

Если наклон я можно определить, истинную массу можно получить из рассчитанной минимальной массы, используя следующее соотношение:

Вероятно, наименьшая масса черной дыры приблизительно равна Планковская масса (о 2.2×10−8 кг или 22 микрограммы ).

Экзопланеты

Ориентация перехода на Землю

Угол наклона, который с Земли казался бы плоским на зеленой плоскости.

У большинства звезд планеты не будут выстроены в линию и ориентированы таким образом, чтобы они затмевались над центром звезды и давали зрителю на Земле идеальный переход. Именно по этой причине мы часто можем экстраполировать только минимальную массу при наблюдении за колебанием звезды, потому что мы не знаем наклон и, следовательно, можем вычислить только часть, тянущую звезду в плоскости небесной сферы.

Для орбитальных тел вне Солнечной системы планетные системы наклон 0 ° или 180 ° соответствует орбите с торца (которую нельзя наблюдать по радиальной скорости), тогда как наклон 90 ° соответствует орбите с ребра (для которой истинная масса равна минимальной массе) .[4]

Основная статья: Способы обнаружения экзопланет

Планеты, орбиты которых сильно наклонены к лучу зрения с Земли, производят меньшие видимые колебания, и поэтому их труднее обнаружить. Одним из преимуществ метода лучевых скоростей является то, что эксцентриситет орбиты планеты можно измерить напрямую. Одним из основных недостатков метода лучевых скоростей является то, что он может оценить только минимальную массу планеты (). Это называется Грех я вырождение. Апостериорное распределение угла наклона я зависит от истинного распределения масс планет.[5]

Радиально-скоростной метод

Однако, когда в системе есть несколько планет, которые вращаются относительно близко друг к другу и имеют достаточную массу, анализ орбитальной стабильности позволяет ограничить максимальную массу этих планет. Метод лучевых скоростей может быть использован для подтверждения результатов, сделанных метод транзита. Когда оба метода используются в сочетании, тогда истинная масса можно оценить.

Хотя лучевая скорость звезды дает только минимальную массу планеты, если ее спектральные линии можно отличить от спектральных линий звезды, тогда можно найти лучевую скорость самой планеты, и это дает наклон орбиты планеты. Это позволяет измерить фактическую массу планеты. Это также исключает ложные срабатывания, а также предоставляет данные о составе планеты. Основная проблема в том, что такое обнаружение возможно только в том случае, если планета вращается вокруг относительно яркой звезды и если планета отражает или излучает много света.[6]

Термин истинная масса является синонимом термина масса, но используется в астрономии, чтобы отличить измеренную массу планеты от минимальной массы, обычно получаемой с помощью методов радиальной скорости.[7] Методы, используемые для определения истинной массы планеты, включают измерение расстояния и периода одной из ее планет. спутники,[8] передовой астрометрия техники, использующие движения других планет в том же звездная система,[7] сочетание методов радиальной скорости с транзит наблюдения (которые указывают на очень низкие орбитальные наклонения),[9] и сочетая методы радиальной скорости с звездный параллакс измерения (которые также определяют наклоны орбиты).[10]

Использование синусоидальной функции

Основная статья: Синус
Единичный круг: радиус имеет длину 1. Переменная т измеряет угол упоминается как θ в тексте.

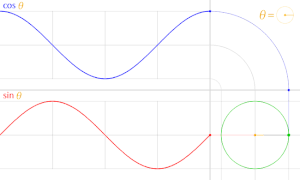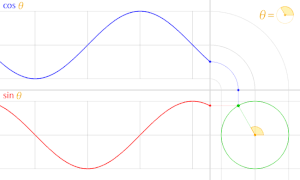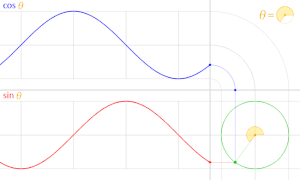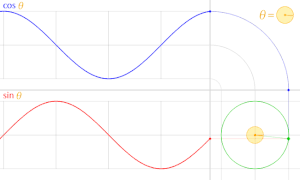
В тригонометрия, единичный круг - это круг радиуса один с центром в начале координат (0, 0) в Декартова система координат.

Проведите линию через начало координат, составляющую угол θ с положительной половиной Икс-оси пересекают единичную окружность. В Икс- и у-координаты этой точки пересечения равны cos (θ) и грех (θ), соответственно. Расстояние точки от начала координат всегда равно 1.

Анимация, показывающая, как функционирует синус (красным) построено на графике из у-координата (красная точка) точки на единичный круг (зеленым) под углом θ.

Звезды

Основная статья: Звездная масса

С массой всего в 93 раза больше, чем у Юпитер (MJ ), или 0,09M☉, AB Doradus C, компаньон AB Doradus A, является самой маленькой известной звездой, в ядре которой происходит ядерный синтез.[11] Для звезд с металличностью, подобной Солнцу, теоретическая минимальная масса, которую звезда может иметь, но все еще подвергаться слиянию в ядре, оценивается примерно в 75 MJ.[12][13] Однако, когда металличность очень низкая, недавнее исследование самых тусклых звезд показало, что минимальный размер звезды составляет около 8,3% солнечной массы, или около 87 MJ.[13][14] Меньшие тела называются коричневые карлики, которые занимают плохо очерченную серую область между звездами и газовые гиганты.

Черные дыры

Основная статья: Микро черная дыра

В принципе, черная дыра может иметь любую массу, равную или превышающую массу Планка (около 2.2×10−8 кг или 22 микрограммы ).[15] Чтобы создать черную дыру, нужно сконцентрировать массу или энергию достаточно, чтобы скорость убегания из региона, в котором он сконцентрирован, превышает скорость света. Это условие дает Радиус Шварцшильда, р = 2GM/c2, куда грамм это гравитационная постоянная, c это скорость света, и M масса черной дыры. С другой стороны, Комптоновская длина волны, λ = час/Mc, куда час это Постоянная Планка, представляет собой ограничение на минимальный размер области, в которой масса M в покое может быть локализован. Для достаточно малых Mприведенная комптоновская длина волны (λ = час/Mc, куда час это приведенная постоянная Планка ) превышает половину радиуса Шварцшильда, и описания черной дыры не существует. Таким образом, эта наименьшая масса черной дыры приблизительно равна массе Планка.

Некоторые расширения современной физики постулируют существование дополнительных измерений пространства. В многомерном пространстве-времени сила гравитации увеличивается быстрее с уменьшением расстояния, чем в трехмерном. При определенных особых конфигурациях дополнительных измерений этот эффект может снизить планковский масштаб до диапазона ТэВ. Примеры таких расширений включают большие дополнительные размеры, частные случаи Модель Рэндалла – Сундрама, и теория струн конфигурации, подобные решениям GKP. В таких сценариях образование черных дыр могло бы стать важным и наблюдаемым эффектом на Большой адронный коллайдер (БАК).[16][17][18][19][20] Это также было бы обычным природным явлением, вызванным космические лучи.

Все это предполагает, что теория общая теория относительности остается в силе на этих малых расстояниях. Если это не так, то другие, в настоящее время неизвестные эффекты ограничивают минимальный размер черной дыры. Элементарные частицы обладают квантово-механическим внутренним угловой момент (вращение ). Правильный закон сохранения для полного (орбитального плюс спин) углового момента вещества в искривленном пространстве-времени требует, чтобы пространство-время было оснащено кручение. Самая простая и естественная теория гравитации с кручением - это Теория Эйнштейна – Картана.[21][22] Кручение изменяет Уравнение Дирака при наличии гравитационного поля и причин фермион частицы должны быть расширены в пространстве.[23]

Пространственное расширение фермионов ограничивает минимальную массу черной дыры порядка 1016 кг, показывая, что микрочерные дыры могут не существовать. Энергия, необходимая для создания такой черной дыры, на 39 порядков больше энергии, доступной на Большом адронном коллайдере, что указывает на то, что LHC не может производить мини-черные дыры. Но если черные дыры образуются, то общая теория относительности оказывается неверной и не существует на таких малых расстояниях. Правила общей теории относительности будут нарушены, поскольку это согласуется с теориями о том, как материя, пространство и время распадаются вокруг горизонт событий черной дыры. Это также доказало бы, что пространственные расширения пределов фермионов неверны. Пределы фермионов предполагают минимальную массу, необходимую для поддержания черной дыры, в отличие от противоположной минимальной массы, необходимой для запуска черной дыры, что теоретически достижимо в LHC.[24]

Рекомендации

  1. ^ Кучнер, Марк Дж. (Сентябрь 2004 г.). «Внесолнечная туманность минимальной массы». Американское астрономическое общество. 612 (2): 1147–1151. arXiv:Astro-ph / 0405536. Bibcode:2004ApJ ... 612.1147K. Дои:10.1086/422577.
  2. ^ Б. Арбутина (июнь 2007 г.). «Минимальное отношение масс двойных систем типа W UMa». Ежемесячные уведомления Королевского астрономического общества. 377 (4): 1635–1637. Bibcode:2007МНРАС.377.1635А. Дои:10.1111 / j.1365-2966.2007.11723.x.
  3. ^ Ротери, Дэвид А .; Гилмор, Иэн; Сефтон, Марк А. (март 2018 г.). Введение в астробиологию. С. 234–236. ISBN  9781108430838.
  4. ^ Флейш, Даниэль; Крегенов, Юлия (29 августа 2013 г.). Пособие для студентов по математике астрономии. С. 97–101. ISBN  9781107610217.
  5. ^ Стивенс, Дэниел Дж .; Гауди, Б. Скотт (2013). «Апостериорные транзитные вероятности». Публикации Тихоокеанского астрономического общества. 125 (930): 933–950. arXiv:1305.1298. Bibcode:2013PASP..125..933S. Дои:10.1086/672572.
  6. ^ Родлер, Флориан; Лопес-Моралес, Мерседес; Рибас, Игнаси (2012). "Взвешивание непереходящего горячего Юпитера Tau BOO b". Астрофизический журнал. 753 (1): L25. arXiv:1206.6197. Bibcode:2012ApJ ... 753L..25R. Дои:10.1088 / 2041-8205 / 753/1 / L25.
  7. ^ а б "Астрономы обсерватории Макдональд открывают планету размером с Нептун с помощью телескопа Хобби-Эберли". Техасский университет в Остине. 31 августа 2004 г. Архивировано с оригинал 13 февраля 2007 г.. Получено 4 сентября 2007.
  8. ^ Браун, Майкл Э.; Шаллер, Эмили Л. (15 июня 2007 г.). «Масса карликовой планеты Эрида». Наука. 316 (5831): 1585. Bibcode:2007Научный ... 316.1585B. Дои:10.1126 / science.1139415. PMID  17569855.
  9. ^ "Как мы узнаем плотность некоторых внесолнечных планет?". Интересно насчет астрономии ?. Архивировано из оригинал 12 октября 2007 г.. Получено 8 сентября 2007.
  10. ^ Хан, Инву; Блэк, Дэвид К .; Гейтвуд, Джордж (2001). "Предварительные астрометрические массы предлагаемых внесолнечных планетных спутников". Письма в астрофизический журнал. 548 (1): L57 – L60. Bibcode:2001ApJ ... 548L..57H. Дои:10.1086/318927.
  11. ^ «Взвешивание самых маленьких звезд», Пресс-релиз Европейской южной обсерватории, ESO: 2, 1 января 2005 г., Bibcode:2005eso..pres .... 2., получено 13 августа 2006.
  12. ^ Босс, Алан (3 апреля 2001 г.), Это планеты или что?, Вашингтонский институт Карнеги, архив из оригинал 28 сентября 2006 г., получено 8 июн 2006.
  13. ^ а б Шига, Дэвид (17 августа 2006 г.), Обнаружен массовый разрыв между звездами и коричневыми карликами, Новый ученый, заархивировано из оригинал 14 ноября 2006 г., получено 23 августа 2006.
  14. ^ Хаббл видит самые слабые звезды, BBC, 18 августа 2006 г., получено 22 августа 2006.
  15. ^ Хокинг, Стивен В. (1971). «Гравитационно коллапсированные объекты очень малой массы». Ежемесячные уведомления Королевского астрономического общества. 152: 75. Bibcode:1971МНРАС.152 ... 75Н. Дои:10.1093 / мнрас / 152.1.75.
  16. ^ Carr, B.J .; Гиддингс, С. Б. (2005). «Квантовые черные дыры». Scientific American. 292 (5): 48–55. Bibcode:2005SciAm.292e..48C. Дои:10.1038 / scientificamerican0505-48. PMID  15882021.
  17. ^ Giddings, S. B .; Томас, С. Д. (2002). «Коллайдеры высоких энергий как фабрики черных дыр: конец физики на малых расстояниях». Физический обзор D. 65 (5): 056010. arXiv:hep-ph / 0106219. Bibcode:2002ПхРвД..65э6010Г. Дои:10.1103 / PhysRevD.65.056010.
  18. ^ Dimopoulos, S .; Ландсберг, Г. Л. (2001). «Черные дыры на Большом адронном коллайдере». Письма с физическими проверками. 87 (16): 161602. arXiv:hep-ph / 0106295. Bibcode:2001ПхРвЛ..87п1602Д. Дои:10.1103 / PhysRevLett.87.161602. PMID  11690198.
  19. ^ Джонсон, Джордж (11 сентября 2001 г.). «Физики стремятся построить черную дыру». Нью-Йорк Таймс. Получено 12 мая 2010.
  20. ^ «Дело о мини-черных дырах». ЦЕРН Курьер. Ноябрь 2004 г.
  21. ^ Sciama, Деннис В. (1964). «Физическая структура общей теории относительности». Обзоры современной физики. 36 (1): 463–469. Bibcode:1964РвМП ... 36..463С. Дои:10.1103 / revmodphys.36.463.
  22. ^ Киббл, Том В. Б. (1961). «Лоренц-инвариантность и гравитационное поле». Журнал математической физики. 2 (2): 212–221. Bibcode:1961JMP ..... 2..212K. Дои:10.1063/1.1703702.
  23. ^ Поплавский, Никодем Я. (2010). «Несингулярные дираковские частицы в пространстве-времени с кручением». Письма по физике B. 690 (1): 73–77. arXiv:0910.1181. Bibcode:2010ФЛБ..690 ... 73П. Дои:10.1016 / j.physletb.2010.04.073.
  24. ^ Стивен Хокинг, "новое предупреждение о судном дне"