Теорема Нильсена – Шрайера - Nielsen–Schreier theorem
В теория групп, раздел математики, Теорема Нильсена – Шрайера заявляет, что каждый подгруппа из свободная группа сам по себе бесплатный.[1][2][3] Он назван в честь Якоб Нильсен и Отто Шрайер.
Формулировка теоремы
Свободная группа может быть определена из групповая презентация состоящий из набор генераторов без отношений. То есть каждый элемент является произведением некоторой последовательности образующих и их обратных, но эти элементы не подчиняются никаким уравнениям, кроме тех, которые тривиально следуют из gg−1 = 1. Элементы свободной группы можно описать как всевозможные сокращенные слова, те струны генераторов и их обратных, в которых ни один генератор не смежен со своим собственным обратным. Два сокращенных слова можно умножить на сцепление их, а затем удаляя любые пары генератор-инверсия, которые возникают в результате объединения.
В Теорема Нильсена – Шрайера заявляет, что если ЧАС является подгруппой свободной группы грамм, тогда ЧАС сам по себе изоморфный в свободную группу. То есть существует набор S элементов, которые создают ЧАС, без нетривиальных соотношений между элементами S.
В Формула Нильсена – Шрайера, или же Формула индекса Шрайера, количественно определяет результат в случае, когда подгруппа имеет конечный индекс: если грамм это свободная группа ранга п (бесплатно на п генераторы), и ЧАС является подгруппой конечных индекс [грамм : ЧАС] = е, тогда ЧАС не имеет звания .[4]
Пример
Позволять грамм быть свободной группой с двумя образующими , и разреши ЧАС - подгруппа, состоящая из всех приведенных слов четной длины (произведений четного числа букв ). потом ЧАС порождается шестью элементами Факторизация любого сокращенного слова в ЧАС в эти образующие и их обратные могут быть построены просто путем взятия последовательных пар букв в сокращенном слове. Однако это не бесплатная презентация ЧАС потому что последние три генератора могут быть записаны в терминах первых трех как . Скорее, ЧАС создается как свободная группа тремя элементами которые не имеют между собой отношений; или вместо этого несколькими другими тройками из шести генераторов.[5] Дальше, грамм бесплатно на п = 2 генератора, ЧАС имеет индекс е = [грамм : ЧАС] = 2 дюйма грамм, и ЧАС бесплатно на 1 + е(п–1) = 3 генератора. Теорема Нильсена – Шрайера утверждает, что подобное ЧАС, каждая подгруппа свободной группы может быть сгенерирована как свободная группа, и если индекс ЧАС конечно, его ранг определяется формулой индекса.
Доказательство
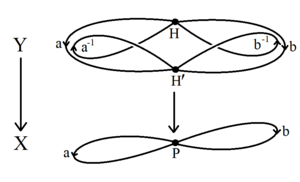
Краткое доказательство теоремы Нильсена – Шрайера использует алгебраическая топология из фундаментальные группы и покрытия пространства.[1] Свободная группа грамм на множестве образующих является фундаментальной группой букет кругов, а топологический граф Икс с единственной вершиной и с петлей-ребром для каждого образующего.[6] Любая подгруппа ЧАС фундаментальной группы есть фундаментальная группа связного накрывающего пространства Y → ИКС. Космос Y является (возможно бесконечным) топологическим графом, Граф смежного класса Шрайера имея по одной вершине для каждого смежный в Г / ч.[7] В любом связном топологическом графе можно сжать ребра остовное дерево графа, создавая букет кругов с та же фундаментальная группа ЧАС. С ЧАС является основной группой букета кругов, она сама по себе свободна.[6]
Симплициальные гомологии позволяет вычислить ранг ЧАС, что равно час1(Y), первый Бетти число покрытия, количество независимых циклов. За грамм без ранга п, график Икс имеет п ребра и 1 вершина; предполагая ЧАС имеет конечный индекс [грамм : ЧАС] = е, покрывающий граф Y имеет en края и е вершины. Первое число Бетти графа равно количеству ребер минус количество вершин плюс количество связанных компонентов; отсюда и ранг ЧАС является:
Это доказательство связано с Райнхольд Баер и Фридрих Леви (1936 ); исходное доказательство Шрайера формирует граф Шрайера другим способом как частное от Граф Кэли из грамм по модулю действия ЧАС.[8]
В соответствии с Лемма Шрайера о подгруппах, набор генераторов для бесплатного представления ЧАС может быть построен из циклы в покрывающем графе, образованном путем конкатенации пути связующего дерева от базовой точки (смежного класса идентичности) к одному из смежных классов, одного ребра, не являющегося деревом, и обратного пути связующего дерева от другой конечной точки ребра обратно к базовая точка.[9][8]
Аксиоматические основы
Хотя известно несколько различных доказательств теоремы Нильсена – Шрайера, все они зависят от аксиома выбора. В доказательстве, основанном, например, на фундаментальных группах букетов, аксиома выбора появляется под видом утверждения, что каждый связный граф имеет остовное дерево. Использование этой аксиомы необходимо, поскольку существуют модели Теория множеств Цермело – Френкеля в котором аксиома выбора и теорема Нильсена – Шрайера неверны. Теорема Нильсена – Шрайера, в свою очередь, влечет более слабую версию аксиомы выбора для конечных множеств.[10][11]
История
Теорема Нильсена – Шрайера - это неабелев аналог более старого результата Ричард Дедекинд, что каждая подгруппа свободная абелева группа бесплатно абелевский.[3]
Якоб Нильсен (1921 ) первоначально доказал ограниченную форму теоремы, утверждающую, что любая конечно порожденная подгруппа свободной группы свободна. Его доказательство включает в себя выполнение последовательности Преобразования Нильсена на порождающем множестве подгруппы, которые уменьшают свою длину (как сокращенные слова в свободной группе, из которой они взяты).[1][12] Отто Шрайер доказал теорему Нильсена – Шрайера в ее полной общности в своей работе 1926 г. абилитация Тезис, Die Untergruppen der freien Gruppe, также опубликовано в 1927 г. в Abh. математика. Сем. Гамбург. Univ.[13][14]
Топологическое доказательство, основанное на фундаментальных группах букетов окружностей, связано с Райнхольд Баер и Фридрих Леви (1936 ). Еще одно топологическое доказательство, основанное на Теория Басса – Серра из групповые действия на деревья, был опубликован Жан-Пьер Серр (1970 ).[15]
Смотрите также
- Основная теорема циклических групп, аналогичный результат для циклические группы что в бесконечном случае можно рассматривать как частный случай теоремы Нильсена – Шрайера
Примечания
- ^ а б c Стиллвелл (1993), Раздел 2.2.4, Теорема Нильсена – Шрайера, стр. 103–104.
- ^ Магнус, Карасс и Солитэр, 1976, Следствие 2.9, с. 95.
- ^ а б Джонсон (1980), Раздел 2, Теорема Нильсена – Шрайера, стр. 9–23.
- ^ Фрид и Джарден (2008), п. 355
- ^ Джонсон (1997), бывший. 15, стр. 12.
- ^ а б Стиллвелл (1993), Раздел 2.1.8, «Свобода генераторов», с. 97.
- ^ Стиллвелл (1993), Раздел 2.2.2, Свойство подгруппы, стр. 100–101.
- ^ а б Боллобас, Бела (1998). «Глава VIII.1». Современная теория графов. Springer Verlag. п. 262. ISBN 978-0-387-98488-9.
- ^ Стиллвелл (1993), Раздел 2.2.6, Трансверсали Шрайера, стр. 105–106.
- ^ Ляухли (1962)
- ^ Ховард (1985).
- ^ Магнус, Карасс и Солитэр, 1976, Раздел 3.2, Процесс восстановления, стр. 121–140.
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., "Теорема Нильсена – Шрайера", Архив истории математики MacTutor, Сент-Эндрюсский университет.
- ^ Хансен, Ван Лундсгаард (1986), Якоб Нильсен, Сборник статей по математике: 1913-1932 гг., Биркхойзер, стр. 117, ISBN 978-0-8176-3140-6.
- ^ Ротман (1995), Теорема Нильсена – Шрайера, стр. 383–387.
Рекомендации
- Баер, Рейнхольд; Леви, Фридрих (1936), "Freie Produkte und ihre Untergruppen", Compositio Mathematica, 3: 391–398.
- Фрид, Майкл Д.; Джарден, Моше (2008), Полевая арифметика, Ergebnisse der Mathematik и ихрер Гренцгебиете. 3. Фольге, 11 (3-е изд.), Springer-Verlag, п. 70, ISBN 978-3-540-77269-9, Zbl 1145.12001.
- Говард, Пол Э. (1985), "Подгруппы свободной группы и аксиома выбора", Журнал символической логики, 50 (2): 458–467, Дои:10.2307/2274234, JSTOR 2274234, МИСТЕР 0793126.
- Джонсон, Д. Л. (1980), Темы теории групповых презентаций, Серия лекций Лондонского математического общества, 42, Издательство Кембриджского университета, ISBN 978-0-521-23108-4.
- Джонсон, Д. Л. (1997), Презентации групп, Студенческие тексты Лондонского математического общества, 15 (2-е изд.), Cambridge University Press, ISBN 978-0-521-58542-2.
- Läuchli, Hans (1962), "Auswahlaxiom in der Algebra", Комментарии Mathematici Helvetici, 37: 1–18, Дои:10.1007 / bf02566957, HDL:20.500.11850/131689, МИСТЕР 0143705.
- Магнус, Вильгельм; Каррасс, Авраам; Солитэр, Дональд (1976), Комбинаторная теория групп (2-е изд. Перераб.), Dover Publications.
- Нильсен, Якоб (1921), "Om regning med ikke-kommutative faktorer og dens anvendelse i gruppeteorien", Математика. Тидскрифт Б (на датском), 1921: 78–94, JFM 48.0123.03.
- Ротман, Джозеф Дж. (1995), Введение в теорию групп, Тексты для выпускников по математике, 148 (4-е изд.), Springer-Verlag, ISBN 978-0-387-94285-8.
- Серр, Ж.-П. (1970), Группы Дискретные, Extrait de I'Annuaire du College de France, Париж.
- Серр, Ж.-П. (1980), Деревья, Springer-Verlag, ISBN 3-540-10103-9.
- Стиллвелл, Джон (1993), Классическая топология и комбинаторная теория групп, Тексты для выпускников по математике, 72 (2-е изд.), Springer-Verlag.







