Сумма префикса - Prefix sum
В Информатика, то сумма префикса, совокупная сумма, инклюзивное сканирование, или просто сканировать последовательности чисел Икс0, Икс1, Икс2, ... это вторая последовательность чисел у0, у1, у2, ..., то суммы из префиксы (промежуточные итоги ) входной последовательности:
- у0 = Икс0
- у1 = Икс0 + Икс1
- у2 = Икс0 + Икс1+ Икс2
- ...
Например, префиксные суммы натуральные числа являются треугольные числа:
входные числа 1 2 3 4 5 6 ... префиксные суммы 1 3 6 10 15 21 ...
Суммы префиксов тривиально вычислить в последовательных моделях вычислений, используя формулу уя = уя − 1 + Икся для вычисления каждого выходного значения в порядке следования. Однако, несмотря на простоту вычислений, префиксные суммы являются полезным примитивом в некоторых алгоритмах, таких как счетная сортировка,[1][2]и они составляют основу сканировать функция высшего порядка в функциональное программирование языков. Суммы префиксов также широко изучались в параллельные алгоритмы, и как решаемая тестовая задача, и как полезный примитив для использования в качестве подпрограммы в других параллельных алгоритмах.[3][4][5]
Абстрактно префиксная сумма требует только бинарный ассоциативный оператор ⊕, что делает его полезным для многих приложений из расчета хорошо разделенные парные разложения точек на обработку строки.[6][7]
Математически операцию взятия префиксных сумм можно обобщить от конечных до бесконечных последовательностей; в этом контексте сумма префикса известна как частичная сумма из серии. Форма суммирования по префиксу или частичного суммирования линейные операторы на векторные пространства конечных или бесконечных последовательностей; их обратные конечная разница операторы.
Сканировать функцию высшего порядка
В функциональное программирование термины, сумма префикса может быть обобщена для любой двоичной операции (не только для добавление операция); в функция высшего порядка полученный в результате этого обобщения, называется сканировать, и он тесно связан с складывать операция. И сканирование, и операции сворачивания применяют данную бинарную операцию к одной и той же последовательности значений, но отличаются тем, что сканирование возвращает всю последовательность результатов бинарной операции, тогда как сворачивание возвращает только окончательный результат. Например, последовательность факториал числа могут быть сгенерированы сканированием натуральных чисел с использованием умножения вместо сложения:
входные числа 1 2 3 4 5 6 ... префиксные продукты 1 2 6 24 120 720 ...
Инклюзивные и эксклюзивные сканы
Язык программирования и библиотечные реализации сканирования могут быть либо включающий или же эксклюзивный. Инклюзивное сканирование включает ввод Икся при вычислении вывода уя (т.е. ), а исключительное сканирование - нет (т. е. ). В последнем случае реализации либо оставляют у0 undefined или примите отдельный "Икс−1"значение, которым нужно заполнить сканирование. Эксклюзивное сканирование является более общим в том смысле, что инклюзивное сканирование всегда может быть реализовано в терминах эксклюзивного сканирования (путем последующего объединения Икся с уя), но исключительное сканирование не всегда может быть реализовано как инклюзивное сканирование, как в случае, когда ⊕ Максимум.
В следующей таблице приведены примеры включенных и эксклюзивных функций сканирования, предоставляемых несколькими языками программирования и библиотеками:
Язык / библиотека Инклюзивное сканирование Эксклюзивное сканирование Haskell scanl1сканлMPI MPI_ScanMPI_ExscanC ++ std :: inclusive_scanstd :: exclusive_scanScala сканироватьРжавчина сканировать
Параллельные алгоритмы
Есть два ключевых алгоритма для параллельного вычисления суммы префикса. Первый предлагает короче охватывать и больше параллелизм но не работает эффективно. Второй вариант эффективен в работе, но требует удвоения диапазона и меньшего параллелизма. Они по очереди представлены ниже.
Алгоритм 1: более короткий промежуток, более параллельный

Хиллис и Стил представим следующий параллельный алгоритм суммирования префиксов:[8]
- за к делать
- за к делать параллельно
- если тогда
- еще
- если тогда
- за к делать параллельно
Выше обозначения означает ценность jth элемент массива Икс в срок я.
Данный п процессоров для выполнения каждой итерации внутреннего цикла за постоянное время, алгоритм в целом выполняется в О(бревно п) time, количество итераций внешнего цикла.
Алгоритм 2: Эффективная работа

Эффективную для работы сумму параллельных префиксов можно вычислить с помощью следующих шагов.[3][9][10]
- Вычислите суммы последовательных пар элементов, в которых первый элемент пары имеет четный индекс: z0 = Икс0 + Икс1, z1 = Икс2 + Икс3, так далее.
- Рекурсивно вычислить сумму префикса ш0, ш1, ш2, ... последовательности z0, z1, z2, ...
- Выразите каждый член последней последовательности у0, у1, у2, ... как сумму до двух членов этих промежуточных последовательностей: у0 = Икс0, у1 = z0, у2 = z0 + Икс2, у3 = ш0и т. д. После первого значения каждое последующее число уя либо копируется с позиции на половину ш последовательность, или предыдущее значение добавлено к одному значению в Икс последовательность.
Если входная последовательность имеет п шагов, то рекурсия продолжается до глубины О(бревно п), что также является ограничением времени параллельной работы этого алгоритма. Количество шагов алгоритма О(п), и его можно реализовать на параллельная машина с произвольным доступом с О(п/бревно п) процессоров без какого-либо асимптотического замедления за счет присвоения нескольких индексов каждому процессору в циклах алгоритма, для которых элементов больше, чем процессоров.[3]
Обсуждение
Каждый из предыдущих алгоритмов работает в О(бревно п) время. Однако первое занимает ровно бревно2 п шагов, а последнее требует 2 журнала2 п − 2 шаги. Для проиллюстрированных примеров с 16 входами алгоритм 1 является 12-сторонним параллельным (49 единиц работы, разделенных на интервал 4), в то время как алгоритм 2 является только 4-сторонним параллельным (26 единиц работы, разделенных на интервал, равный 6). Однако алгоритм 2 эффективен с точки зрения работы - он выполняет только постоянный коэффициент (2) объема работы, требуемой последовательным алгоритмом - в то время как алгоритм 1 работает неэффективно - он выполняет асимптотически больше работы (логарифмический коэффициент), чем требуется. последовательно. Следовательно, алгоритм 1, вероятно, будет работать лучше, когда доступен обширный параллелизм, но алгоритм 2, вероятно, будет работать лучше, когда параллелизм более ограничен.
Параллельные алгоритмы для сумм префиксов часто можно обобщить для других операций сканирования на ассоциативные бинарные операции,[3][4] и их также можно эффективно вычислить на современном параллельном оборудовании, таком как GPU.[11] Идея встроить в аппаратную часть функционального блока, предназначенного для вычисления многопараметрической префиксной суммы, была запатентована Узи Вишкин.[12]
Многие параллельные реализации следуют двухпроходной процедуре, при которой частичные суммы префиксов вычисляются на первом проходе на каждом процессоре; затем вычисляется префиксная сумма этих частичных сумм и передается обратно в блоки обработки для второго прохода с использованием теперь известного префикса в качестве начального значения. Асимптотически этот метод требует примерно двух операций чтения и одной операции записи для каждого элемента.
Конкретные реализации алгоритмов суммы префиксов
Реализация параллельного алгоритма суммирования префиксов, как и другие параллельные алгоритмы, должна принимать архитектура распараллеливания платформы. В частности, существует несколько алгоритмов, адаптированных для платформ, работающих на Общая память а также алгоритмы, которые хорошо подходят для платформ, использующих распределенная память, надеется передача сообщений как единственная форма межпроцессного взаимодействия.
Следующий алгоритм предполагает Общая память модель машины; все элементы обработки (PE) имеют доступ к одной и той же памяти. Версия этого алгоритма реализована в многоядерной стандартной библиотеке шаблонов (MCSTL),[13][14] параллельная реализация Стандартная библиотека шаблонов C ++ который предоставляет адаптированные версии для параллельных вычислений различных алгоритмов.
Чтобы одновременно вычислить сумму префикса по элементы данных с элементы обработки, данные делятся на блоки, каждый из которых содержит элементов (для простоты считаем, что разделяет ). Обратите внимание, что хотя алгоритм делит данные на блоки, только элементы обработки работают параллельно.
В первом цикле каждый PE вычисляет локальную сумму префиксов для своего блока. Последний блок вычислять не нужно, поскольку эти суммы префиксов рассчитываются только как смещения к суммам префиксов последующих блоков, а последний блок по определению не выполняется.
В смещения, которые хранятся в последней позиции каждого блока, накапливаются в собственной сумме префиксов и сохраняются в своих последующих позициях. За будучи небольшим числом, быстрее делать это последовательно, для больших , этот шаг также можно было бы выполнить параллельно.
Выполняется вторая развертка. На этот раз первый блок не нужно обрабатывать, так как не нужно учитывать смещение предыдущего блока. Однако в этот цикл вместо него включается последний блок, и суммы префиксов для каждого блока вычисляются с учетом смещений блоков суммы префиксов, вычисленных в предыдущем цикле.
функция prefix_sum(элементы) { п := размер(элементы) п := номер из обработка элементы prefix_sum := [0...0] из размер п делать параллельно я = 0 к п-1 { // i: = индекс текущего PE из j = я * п / (п+1) к (я+1) * п / (п+1) - 1 делать { // Сохраняет только префиксную сумму локальных блоков store_prefix_sum_with_offset_in(элементы, 0, prefix_sum) } } Икс = 0 за я = 1 к п { Икс += prefix_sum[я * п / (п+1) - 1] // Строим префиксную сумму по первым p блокам prefix_sum[я * п / (п+1)] = Икс // Сохраняем результаты для использования в качестве смещений во второй развертке } делать параллельно я = 1 к п { // i: = индекс текущего PE из j = я * п / (п+1) к (я+1) * п / (п+1) - 1 делать { компенсировать := prefix_sum[я * п / (п+1)] // Вычислить сумму префиксов, взяв сумму предыдущих блоков в качестве смещения store_prefix_sum_with_offset_in(элементы, компенсировать, prefix_sum) } } возвращаться prefix_sum}Распределенная память: алгоритм гиперкуба
Алгоритм суммы префиксов гиперкуба[15] хорошо адаптирован для распределенная память платформы и работает с обменом сообщениями между элементами обработки. Предполагается наличие количество элементов процессора (ЭЭ), участвующих в алгоритме, равно количеству углов в -размерный гиперкуб.
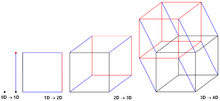
На протяжении всего алгоритма каждый PE рассматривается как угол в гипотетическом гиперкубе со знанием общей суммы префиксов. а также префиксная сумма всех элементов до самого себя (согласно упорядоченным индексам среди PE), оба в своем собственном гиперкубе.
- Алгоритм начинается с предположения, что каждый PE является единственным углом нульмерного гиперкуба и, следовательно, и равны локальной префиксной сумме собственных элементов.
- Алгоритм продолжается путем объединения гиперкубов, смежных по одному измерению. Во время каждого объединения обменивается и агрегируется между двумя гиперкубами, что сохраняет неизменным тот факт, что все PE в углах этого нового гиперкуба хранят общую сумму префиксов этого нового унифицированного гиперкуба в своей переменной . Однако только гиперкуб, содержащий PE с более высоким индексом, также добавляет это к их локальной переменной , сохраняя инвариант, что сохраняет только значение суммы префиксов всех элементов в PE с индексами, меньшими или равными их собственному индексу.
В -мерный гиперкуб с PE по углам, алгоритм нужно повторить раз иметь нульмерные гиперкубы объединяются в один -мерный гиперкуб. дуплексная связь модель, где двух соседних PE в разных гиперкубах можно обмениваться в обоих направлениях за один шаг связи, это означает коммуникационные стартапы.
я := Индекс из собственный процессор элемент (PE)м := префикс сумма из местный элементы из это PEd := номер из размеры из в гипер кубИкс = м; // Неизменяемый: сумма префикса до этого PE в текущем субкубеσ = м; // Неизменяемый: сумма префиксов всех элементов в текущем субкубеза (k=0; k <= d-1; k++) { у = σ @ PE(я xor 2^k) // Получаем общую сумму префиксов противоположного подкуба по измерению k σ = σ + у // Агрегировать сумму префиксов обоих субкубов если (я & 2^k) { Икс = Икс + у // Агрегировать только префиксную сумму из другого субкуба, если этот PE имеет более высокий индекс. }}Сообщения большого размера: конвейерное двоичное дерево
Конвейерный алгоритм двоичного дерева[16] - еще один алгоритм для платформ с распределенной памятью, который особенно хорошо подходит для сообщений большого размера.
Как и алгоритм гиперкуба, он предполагает особую коммуникационную структуру. Элементы обработки (ПЭ) гипотетически расположены в двоичное дерево (например, дерево Фибоначчи) с инфиксная нумерация в соответствии с их индексом в ПЭ. Связь в таком дереве всегда происходит между родительскими и дочерними узлами.
В инфиксная нумерация гарантирует, что для любого данного PEj, индексы всех узлов, достижимых его левым поддеревом меньше чем и индексы всех узлов в правом поддереве больше, чем . Индекс родителя больше любого из индексов в PEjподдерево, если PEj левый ребенок и меньше, если PEj правильный ребенок. Это позволяет рассуждать следующим образом:

- Сумма местного префикса левого поддерева необходимо агрегировать для расчета PEjсумма местного префикса .
- Сумма местного префикса правого поддерева необходимо агрегировать, чтобы вычислить сумму локальных префиксов PE более высокого уровнячас которые достигаются на пути, содержащем левое дочернее соединение (что означает ).
- Общая сумма префикса ЧПj необходимо для вычисления общих сумм префиксов в правом поддереве (например, для узла с наивысшим индексом в поддереве).
- PEj необходимо включить общую сумму префикса первого узла более высокого порядка, который достигается восходящим путем, включая правое дочернее соединение, для вычисления его общей суммы префиксов.
Обратите внимание на различие между суммой локального поддерева и общей суммы префиксов. Точки два, три и четыре могут наводить на мысль, что они образуют круговую зависимость, но это не так. PE более низкого уровня могут потребовать общую сумму префиксов PE более высокого уровня для вычисления их общей суммы префиксов, но PE более высокого уровня требуют только суммы локальных префиксов поддерева для вычисления их общей суммы префиксов. Корневому узлу как узлу самого высокого уровня требуется только локальная сумма префиксов его левого поддерева для вычисления своей собственной суммы префиксов. Каждый PE на пути от PE0 к корневому PE требуется только локальная сумма префиксов его левого поддерева для вычисления своей собственной суммы префиксов, тогда как каждый узел на пути от PEп-1 (последний PE) в PEкорень требует, чтобы общая сумма префиксов своего родителя вычисляла свою собственную общую сумму префиксов.
Это приводит к двухфазному алгоритму:
Восходящая фаза
Распространение суммы локального префикса поддерева своему родителю для каждого PEj.
Нисходящая фаза
Распространение эксклюзивного (эксклюзивного PEj а также PE в его левом поддереве) общая сумма префиксов всех PE с более низким индексом, которые не включены в адресуемое поддерево PEj в PE нижнего уровня в левом дочернем поддереве PEj. Распространение включающей префиксной суммы к правому дочернему поддереву PEj.
Обратите внимание, что алгоритм выполняется параллельно на каждом PE, и PE будут блокироваться при получении, пока их дети / родители не предоставят им пакеты.
k := номер из пакеты в а сообщение м из а PEм @ {оставили, верно, родитель, это} := // Сообщения на разных PEИкс = м @ это// Фаза увеличения - вычисление суммы локальных префиксов поддереваза j=0 к k-1: // Конвейерная обработка: для каждого пакета сообщения если hasLeftChild: блокировка получить м[j] @ оставили // Это заменяет локальный m [j] полученным m [j] // Агрегировать включающую локальную сумму префикса из PE с более низким индексом Икс[j] = м[j] ⨁ Икс[j] если hasRightChild: блокировка получить м[j] @ верно // Мы не агрегируем m [j] в локальную префиксную сумму, поскольку правые дочерние элементы являются PE с более высоким индексом Отправить Икс[j] ⨁ м[j] к родитель еще: Отправить Икс[j] к родитель// Нисходящая фазаза j=0 к k-1: м[j] @ это = 0 если hasParent: блокировка получить м[j] @ родитель // Для левого потомка m [j] - это исключающая сумма префикса родителей, для правого дочернего элемента - включающая префиксная сумма Икс[j] = м[j] ⨁ Икс[j] Отправить м[j] к оставили // Общая сумма префиксов всех PE, меньших этого или любого PE в левом поддереве Отправить Икс[j] к верно // Общая сумма префиксов всех PE, меньших или равных этому PEКонвейерная обработка
Если сообщение длины можно разделить на пакеты и оператор ⨁ могут использоваться отдельно для каждого из соответствующих пакетов сообщений, конвейерная обработка возможно.[16]
Если алгоритм используется без конвейерной обработки, всегда работают только два уровня (отправляющие PE и принимающие PE) двоичного дерева, в то время как все остальные PE ожидают. Если есть элементы обработки и сбалансированное бинарное дерево, дерево имеет уровней, длина пути от к следовательно является который представляет максимальное количество непараллельных коммуникационных операций во время восходящей фазы, аналогично, связь по нисходящему пути также ограничена стартапы. Предполагая, что время запуска связи составляет и время побайтовой передачи , восходящая и нисходящая фазы ограничены в сценарии без конвейера.
После разделения на k пакетов, каждый размером и отправляя их по отдельности, первый пакет все еще нуждается в быть распространенным на как часть суммы локального префикса, и это будет повторяться для последнего пакета, если . Однако между ними все PE на пути могут работать параллельно, и каждая третья операция связи (прием слева, прием справа, отправка родительскому) отправляет пакет на следующий уровень, так что одна фаза может быть завершена за коммуникационные операции и обе фазы вместе требуют что подходит для сообщений большого размера .
Алгоритм можно дополнительно оптимизировать, используя полнодуплексная или телефонная модель общение и наложение восходящей и нисходящей фаз.[16]
Структуры данных
Когда набор данных может обновляться динамически, он может храниться в Фенвик дерево структура данных. Эта структура позволяет как искать любое индивидуальное значение суммы префикса, так и изменять любое значение массива за логарифмическое время за операцию.[17] Однако более ранняя статья 1982 г. [18] представляет структуру данных, называемую деревом частичных сумм (см. раздел 5.1), которая, кажется, перекрывает деревья Фенвика; в 1982 году термин «префикс-сумма» еще не был так распространен, как сегодня.
Для многомерных массивов таблица суммированных площадей предоставляет структуру данных, основанную на суммах префиксов для вычисления сумм произвольных прямоугольных подмассивов. Это может быть полезным примитивом в свертка изображения операции.[19]
Приложения
Счетная сортировка является целочисленная сортировка алгоритм, который использует префиксную сумму гистограмма частот клавиш для вычисления позиции каждого ключа в отсортированном выходном массиве. Он работает за линейное время для целочисленных ключей, которые меньше количества элементов, и часто используется как часть радиальная сортировка, быстрый алгоритм сортировки целых чисел, размер которых менее ограничен.[1]
Рейтинг списка, проблема преобразования связанный список в множество который представляет ту же последовательность элементов, можно рассматривать как вычисление суммы префикса для последовательности 1, 1, 1, ... и последующее отображение каждого элемента в позицию массива, заданную его значением суммы префикса; путем комбинирования рейтинга списков, сумм префиксов и Эйлер туры, много важных задач по деревья может быть решена с помощью эффективных параллельных алгоритмов.[4]
Раннее применение параллельных алгоритмов суммирования префиксов было в разработке двоичные сумматоры, Логические схемы, которые могут складывать два п-битовые двоичные числа. В этом приложении последовательность битов переноса сложения может быть представлена как операция сканирования последовательности пар входных битов с использованием функция большинства чтобы объединить предыдущий перенос с этими двумя битами. Каждый бит выходного числа затем можно найти как Эксклюзивный или двух входных битов с соответствующим битом переноса. Используя схему, которая выполняет операции параллельного алгоритма суммы префиксов, можно разработать сумматор, который использует О(п) логические ворота и О(бревно п) временные шаги.[3][9][10]
в параллельная машина с произвольным доступом В модели вычислений суммы префиксов могут использоваться для моделирования параллельных алгоритмов, которые предполагают возможность одновременного доступа нескольких процессоров к одной и той же ячейке памяти на параллельных машинах, которые запрещают одновременный доступ. С помощью сортировочная сеть, набор запросов параллельного доступа к памяти может быть упорядочен в последовательность, так что доступ к одной и той же ячейке будет непрерывным в пределах последовательности; Затем операции сканирования могут использоваться для определения того, какой из обращений успешно записывает в запрошенные ячейки, и для распределения результатов операций чтения из памяти на несколько процессоров, которые запрашивают тот же результат.[20]
В Гай Блеллох доктор философии Тезис,[21] параллельные операции с префиксом являются частью формализации Параллелизм данных модель, предоставляемая машинами, такими как Соединительная машина. Соединительная машина CM-1 и CM-2 обеспечивала гиперкубический сеть, в которой может быть реализован описанный выше алгоритм 1, тогда как CM-5 предоставил выделенную сеть для реализации алгоритма 2.[22]
В строительстве Коды Грея, последовательности двоичных значений со свойством, что значения последовательных последовательностей отличаются друг от друга одной битовой позицией, числом п может быть преобразовано в значение кода Грея в позиции п последовательности, просто взяв Эксклюзивный или из п и п/2 (число, образованное сдвигом п справа на одну битовую позицию). Обратная операция, декодирование значения, закодированного по Грею Икс в двоичное число, более сложный, но может быть выражен как префиксная сумма битовИкс, где каждая операция суммирования в префиксной сумме выполняется по модулю два. Сумма префиксов этого типа может быть эффективно выполнена с использованием побитовых логических операций, доступных на современных компьютерах, путем вычисления Эксклюзивный или из Икс с каждым из чисел, образованных сдвигом Икс слева на количество битов, равное степени двойки.[23]
Параллельный префикс (использующий умножение в качестве базовой ассоциативной операции) также может использоваться для построения быстрых алгоритмов параллельного полиномиальная интерполяция. В частности, его можно использовать для вычисления разделенная разница коэффициенты Форма Ньютона интерполяционного полинома.[24] Этот подход, основанный на префиксе, также можно использовать для получения обобщенных разделенных разностей для (конфлюэнтных) Эрмита интерполяция а также для параллельных алгоритмов для Vandermonde системы.[25]
Смотрите также
Рекомендации
- ^ а б Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2001), "8.2 Сортировка подсчета", Введение в алгоритмы (2-е изд.), MIT Press и Макгроу-Хилл, стр. 168–170, ISBN 0-262-03293-7.
- ^ Коул, Ричард; Вишкин, Узи (1986), "Детерминированное подбрасывание монеты с приложениями к оптимальному ранжированию в параллельном списке", Информация и контроль, 70 (1): 32–53, Дои:10.1016 / S0019-9958 (86) 80023-7
- ^ а б c d е Ladner, R.E .; Фишер, М. Дж. (1980), "Вычисление параллельного префикса", Журнал ACM, 27 (4): 831–838, CiteSeerX 10.1.1.106.6247, Дои:10.1145/322217.322232, МИСТЕР 0594702.
- ^ а б c Тарджан, Роберт Э.; Вишкин, Узи (1985), "Эффективный параллельный алгоритм двусвязности", SIAM Журнал по вычислениям, 14 (4): 862–874, Дои:10.1137/0214061.
- ^ Lakshmivarahan, S .; Дхалл, С. (1994), Параллелизм в проблеме префикса, Oxford University Press, ISBN 0-19508849-2.
- ^ Блеллох, парень (2011), Суммы префиксов и их применение (конспекты лекций) (PDF), Университет Карнеги Меллон.
- ^ Каллахан, Пол; Косараджу, С. Рао (1995), "Разложение многомерных наборов точек с приложениями к k-ближайшим соседям и n-частным потенциальным полям", Журнал ACM, 42 (1): 67–90, Дои:10.1145/200836.200853.
- ^ Хиллис, У. Дэниэл; Стил-младший, Гай Л. (декабрь 1986 г.). «Алгоритмы параллельных данных». Коммуникации ACM. 29 (12): 1170–1183. Дои:10.1145/7902.7903.
- ^ а б Офман, Ю. (1962), Об алгоритмической сложности дискретных функций, Доклады Академии Наук СССР (на русском), 145 (1): 48–51, МИСТЕР 0168423. Английский перевод "Об алгоритмической сложности дискретных функций", Советская физика. 7: 589–591 1963.
- ^ а б Храпченко, В. М. (1967), "Асимптотическая оценка времени сложения параллельного сумматора", Проблемы Кибернет. (на русском), 19: 107–122. Английский перевод в Syst. Теория Res. 19; 105–122, 1970.
- ^ Сенгупта, Шубхабрата; Харрис, Марк; Чжан, Яо; Оуэнс, Джон Д. (2007). Примитивы сканирования для вычислений на GPU. Proc. 22-й симпозиум ACM SIGGRAPH / EUROGRAPHICS по графическому оборудованию. С. 97–106. Архивировано из оригинал на 2014-09-03. Получено 2007-11-29.
- ^ Вишкин, Узи (2003). Суммы префиксов и их применение. Патент США 6542918.
- ^ Синглер, Йоханнес. «MCSTL: многоядерная стандартная библиотека шаблонов». Получено 2019-03-29.
- ^ Синглер, Йоханнес; Сандерс, Питер; Путце, Феликс (2007). «MCSTL: многоядерная стандартная библиотека шаблонов». Euro-Par 2007 Параллельная обработка. Конспект лекций по информатике. 4641. С. 682–694. Дои:10.1007/978-3-540-74466-5_72. ISBN 978-3-540-74465-8. ISSN 0302-9743.
- ^ Анант Грама; Випин Кумар; Аншул Гупта (2003). Введение в параллельные вычисления. Эддисон-Уэсли. С. 85, 86. ISBN 978-0-201-64865-2.
- ^ а б c Сандерс, Питер; Träff, Джеспер Ларссон (2006). «Алгоритмы параллельного префикса (сканирования) для MPI». Последние достижения в области параллельных виртуальных машин и интерфейса передачи сообщений. Конспект лекций по информатике. 4192. С. 49–57. Дои:10.1007/11846802_15. ISBN 978-3-540-39110-4. ISSN 0302-9743.
- ^ Фенвик, Питер М. (1994), «Новая структура данных для сводных таблиц частот», Программное обеспечение: практика и опыт, 24 (3): 327–336, Дои:10.1002 / spe.4380240306
- ^ Шилоах, Йосси; Вишкин, Узи (1982б), "Ан О(п2 бревноп) параллельный алгоритм максимального потока », Журнал алгоритмов, 3 (2): 128–146, Дои:10.1016 / 0196-6774 (82) 90013-X
- ^ Szeliski, Ричард (2010), "Суммарная таблица площадей (интегральное изображение)", Компьютерное зрение: алгоритмы и приложения, Texts in Computer Science, Springer, pp. 106–107, ISBN 9781848829350.
- ^ Вишкин, Узи (1983), "Реализация одновременного доступа к адресам памяти в моделях, которые это запрещают", Журнал алгоритмов, 4 (1): 45–50, Дои:10.1016/0196-6774(83)90033-0, МИСТЕР 0689265.
- ^ Блеллох, Гай Э. (1990). Векторные модели для параллельных вычислений с данными. Кембридж, Массачусетс: MIT Press. ISBN 026202313X. OCLC 21761743.
- ^ Лейзерсон, Чарльз Э.; Abuhamdeh, Zahi S .; Дуглас, Дэвид С.; Фейнман, Карл Р .; Ганмукхи, Махеш Н .; Хилл, Джеффри В .; Хиллис, В. Дэниэл; Kuszmaul, Bradley C .; Сен-Пьер, Маргарет А. (15 марта 1996 г.). «Сетевая архитектура соединительной машины CM-5». Журнал параллельных и распределенных вычислений. 33 (2): 145–158. Дои:10.1006 / jpdc.1996.0033. ISSN 0743-7315.
- ^ Уоррен, Генри С. (2003), Хакерское наслаждение, Эддисон-Уэсли, стр. 236, г. ISBN 978-0-201-91465-8.
- ^ Eğeciolu, O .; Gallopoulos, E .; Коч, К. (1990), "Параллельный метод быстрой и практичной интерполяции Ньютона высокого порядка", BIT Компьютерные науки и вычислительная математика, 30 (2): 268–288, Дои:10.1007 / BF02017348.
- ^ Eğeciolu, O .; Gallopoulos, E .; Коч, К. (1989), "Быстрое вычисление разделенных разностей и параллельная интерполяция Эрмита", Журнал сложности, 5 (4): 417–437, Дои:10.1016 / 0885-064X (89) 90018-6





















![{displaystyle mathbb {[l ... j-1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e42e648cab095972c89f5c3cdfd706a6d6542ab)

![{displaystyle mathbb {[j + 1 ... r]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bb02bd7fbd1f725326c3fcdeba81a5b64ea2192)
![{displaystyle mathbb {oplus [l..j-1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/111c0326733e32d7fff1d2436c8f91bd93c2f911)
![{displaystyle mathbb {oplus [l..j]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8540c987feea78fa6b8c24881a0743b47567bf3)
![{displaystyle mathbb {oplus [j + 1..r]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaf861ae0ef24c4ce8902502b30eb173ccee27f9)

![{displaystyle mathbb {oplus [0..j]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce3a3c99c6216685a2b3ecebd478ab7cddd1a185)
![{displaystyle mathbb {oplus [0..j..r]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4a67fa871d710d36cb7e7db6f6202d1938211f8)
![{displaystyle mathbb {oplus [0..l-1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29c0eb618b27e5892fb370b0eb4fdf14a18ed333)
![{displaystyle mathbb {oplus [l..j..r]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77936279f8ecfbcde9d649eff659d5fc0acec03c)













