Стадион (геометрия) - Википедия - Stadium (geometry)

Параметры стадиона
В Бунимович стадион, а хаотичный динамическая система на основе формы стадиона
Дно из этого пластика корзина имеет форму стадиона.

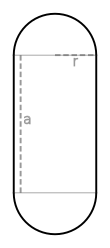
А стадион является двумерным геометрическая форма построен из прямоугольник с полукруги на паре противоположных сторон.[1]Такая же форма известна также как дискорегулятор,[2] окружать,[3][4] или же колбасное тело.[5]

Форма основана на стадион, место, используемое для легкая атлетика и скачки треки.

Стадион может быть построен как Сумма Минковского из диск и отрезок.[5] В качестве альтернативы это район точек на заданном расстоянии от отрезка линии. Стадион - это тип овал. Однако, в отличие от некоторых других овалов, таких как эллипсы, это не алгебраическая кривая потому что разные части его границы определяются разными уравнениями.

Формулы

В периметр площади стадиона рассчитывается по формуле куда а длина прямых сторон и р - радиус полукругов. При тех же параметрах площадь стадиона .[6]

Стадион Бунимовича

Когда эта форма используется при изучении динамический бильярд, это называется Бунимович стадион. Леонид Бунимович использовал эту форму, чтобы показать, что бильярдные дорожки могут демонстрировать хаотичное поведение (положительный Показатель Ляпунова и экспоненциальное расхождение путей) даже внутри выпуклого бильярдного стола.[7]

Связанные фигуры

А капсула производится путем вращения стадиона вокруг линия симметрии который делит пополам полукруги.

Рекомендации

  1. ^ «Стадион - от Wolfram MathWorld». Mathworld.wolfram.com. 2013-01-19. Получено 2013-01-31.
  2. ^ Дзубиэлла, Иоахим; Маттиас Шмидт; Хартмут Лёвен (2000). «Топологические дефекты в каплях нематика твердых сфероцилиндров». Физический обзор E. 62: 5081. arXiv:cond-mat / 9906388. Bibcode:2000PhRvE..62.5081D. Дои:10.1103 / PhysRevE.62.5081.
  3. ^ Аккерманн, Курт. "Obround - Пробивные инструменты - VIP, Inc". www.vista-industrial.com. Получено 2016-04-29.
  4. ^ «Округлое стекло уровнемера: L.J. Star Incorporated». L.J.Star Incorporated. Архивировано из оригинал на 2016-04-22. Получено 2016-04-29.
  5. ^ а б Хуанг, Пинлян; Пан, Шэнлян; Ян, Юньлун (2015). «Положительные центры множества выпуклых кривых». Дискретная и вычислительная геометрия. 54 (3): 728–740. Дои:10.1007 / s00454-015-9715-9. МИСТЕР  3392976.
  6. ^ «Калькулятор стадиона». Calculatorsoup.com. Получено 2013-01-31.
  7. ^ Бунимович, Л.А. (1974). «Эргодические свойства некоторых биллиардов». Функц. Анальный. и Приложен. 8 (3): 73–74. МИСТЕР  0357736.