Древо первобытных пифагорейских троек - Википедия - Tree of primitive Pythagorean triples

Дерево Берггрена примитивных троек Пифагора.

В математика, а дерево первобытных пифагоровых троек это дерево данных в котором каждый узел разветвляется на три последующих узла с бесконечным набором всех узлов, дающих все (и только) примитивы Пифагорейские тройки без дублирования.

Пифагорова тройка - это набор из трех положительных целые числа а, б, и c имея свойство, что они могут быть соответственно двумя ногами и гипотенуза из прямоугольный треугольник, таким образом удовлетворяя уравнению ${ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$; тройка называется примитивный если и только если то наибольший общий делитель из а, б, и c является одним. Примитивная тройка Пифагора а, б, и c также попарно совмещать. Множество всех примитивных пифагоровых троек имеет структуру корневого дерево, в частности тройное дерево, естественным образом. Впервые это было обнаружено Б. Берггреном в 1934 году.^[1]

Ф. Дж. М. Барнинг показал^[2] что когда любой из трех матрицы

${ displaystyle { begin {array} {lcr} A = { begin {bmatrix} 1 & -2 & 2 2 & -1 & 2 2 & -2 & 3 end {bmatrix}} & B = { begin {bmatrix} 1 & 2 & 2 2 & 1 & 2 2 & 2 & 3 end {bmatrix}} & C = { begin {bmatrix} -1 & 2 & 2 - 2 & 1 & 2 - 2 & 2 & 3 end {bmatrix}} end {array}}}$

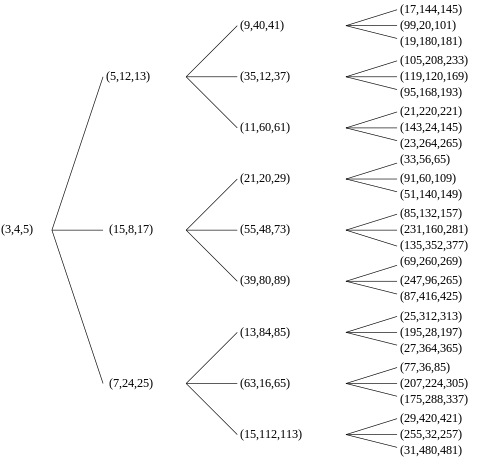
является умноженный справа от вектор столбца компоненты которого образуют пифагорову тройку, то результатом является другой вектор-столбец, компоненты которого являются другой пифагоровой тройкой. Если исходная тройка примитивна, то получится и та, которая получится. Таким образом, каждая примитивная пифагорейская тройка имеет трех «детей». Таким образом, все примитивные пифагорейские тройки произошли от тройки (3, 4, 5), и никакая примитивная тройка не появляется более одного раза. Результат может быть графически представлен в виде бесконечного тернарного дерева с (3, 4, 5) в корневом узле (см. Классическое дерево справа). Это дерево также появилось в работах А. Холла в 1970 г.^[3] и А. Р. Канга в 1990 г.^[4] В 2008 г. В. Е. Фирстов в целом показал, что существует только три таких дерева трихотомии и явно дает дерево, подобное дереву Берггрена, но начиная с начального узла (4, 3, 5).^[5]

Доказательства

Наличие исключительно примитивных пифагоровых троек

Это можно показать индуктивно что дерево содержит примитивные пифагоровы тройки и ничего больше, показывая, что, начиная с примитивной пифагорейской тройки, например, присутствующей в начальном узле с (3, 4, 5), каждая сгенерированная тройка является как пифагоровой, так и примитивной.

Сохранение пифагорейской собственности

Если какая-либо из вышеперечисленных матриц, скажем А, применяется к тройке (а, б, c)^Т обладающий пифагорейским свойством а²+б²=c² чтобы получить новую тройку (d, е, ж)^Т = А(а, б, c)^Т, эта новая тройка тоже пифагорейская. Это можно увидеть, выписав каждый из d, е, и ж как сумма трех слагаемых в а, б, и c, возводя каждый из них в квадрат и подставляя c²=а²+б² чтобы получить ж²=d²+е². Это справедливо для B и C а также для А.

Сохранение примитивности

Матрицы А, B, и C все унимодулярный - то есть они имеют только целые элементы и их определители равны ± 1. Таким образом, их инверсии также унимодулярны и, в частности, имеют только целые элементы. Так что если кто-то из них, например А, применяется к примитивной пифагоровой тройке (а, б, c)^Т чтобы получить еще одну тройку (d, е, ж)^Т, у нас есть (d, е, ж)^Т = А(а, б, c)^Т и поэтому (а, б, c)^Т = А⁻¹(d, е, ж)^Т. Если бы какой-либо простой фактор был разделен между любыми двумя (и, следовательно, всеми тремя) d, е, и ж то по этому последнему уравнению это простое число также делит каждый из а, б, и c. Так что если а, б, и c на самом деле попарно взаимно просты, то d, е, и ж также должны быть попарно взаимно просты. Это справедливо для B и C а также для А.

Наличие каждой примитивной пифагорейской тройки ровно один раз

Чтобы показать, что дерево содержит каждую примитивную тройку Пифагора, но не более одного раза, достаточно показать, что для любой такой тройки существует ровно один путь назад через дерево к начальному узлу (3, 4, 5). В этом можно убедиться, применив по очереди каждую из унимодулярных обратных матриц А⁻¹, B⁻¹, и C⁻¹ произвольной примитивной пифагоровой тройке (d, е, ж), отмечая, что по приведенным выше рассуждениям примитивность и свойство Пифагора сохраняются, и отмечая, что для любой тройки, большей, чем (3, 4, 5), ровно одна из матриц обратных переходов дает новую тройку со всеми положительными элементами (и меньшими гипотенуза). По индукции эта новая действительная тройка сама по себе приводит ровно к одной действительной тройке меньшего размера и т. Д. По конечности числа все меньших и меньших потенциальных гипотенуз в конце концов достигается (3, 4, 5). Это доказывает, что (d, е, ж) действительно встречается в дереве, так как до него можно добраться из (3, 4, 5), изменив шаги; и это происходит однозначно, потому что был только один путь из (d, е, ж) на (3, 4, 5).

Характеристики

Преобразование с использованием матрицы А, если выполняется повторно из (а, б, c) = (3, 4, 5), сохраняет особенность б + 1 = c; матрица B сохраняет а – б = ± 1, начиная с (3, 4, 5); и матрица C сохраняет особенность а + 2 = c начиная с (3, 4, 5).

Геометрическая интерпретация этого дерева включает в себя вне окружности присутствует на каждом узле. Три дочерних элемента любого родительского треугольника «наследуют» свои inradii от родителя: радиусы вневписанной окружности родителя становятся внутренними радиусами для следующего поколения.^[6]:стр.7 Например, родительский элемент (3, 4, 5) имеет радиусы вневписанной окружности, равные 2, 3 и 6. Это в точности внутренние радиусы трех дочерних элементов (5, 12, 13), (15, 8, 17) и (21, 20, 29) соответственно.

Если любой из А или же C применяется многократно из любой тройки Пифагора, используемой в качестве начального условия, тогда динамика любого из а, б, и c можно выразить как динамику Икс в

${ displaystyle x_ {n + 3} -3x_ {n + 2} + 3x_ {n + 1} -x_ {n} = 0 ,}$

который формируется на общих характеристическое уравнение

${ displaystyle lambda ^ {3} -3 lambda ^ {2} +3 lambda -1 = 0. ,}$

Если B применяется многократно, то динамика любого из а, б, и c можно выразить как динамику Икс в

${ displaystyle x_ {n + 3} -5x_ {n + 2} -5x_ {n + 1} + x_ {n} = 0, ,}$

которое построено на характеристическом уравнении B.^[7]

Более того, бесконечное количество других одномерных третьего порядка разностные уравнения можно найти, умножив любую из трех матриц вместе произвольное количество раз в произвольной последовательности. Например, матрица D = CB перемещает один узел из дерева на два узла (поперек, затем вниз) за один шаг; характеристическое уравнение D дает образец для динамики третьего порядка любого из а, б, или же c в неполный дерево, образованноеD.

Альтернативные методы построения дерева

Дерево Прайса примитивных троек Пифагора.

Другой подход к динамике этого дерева^[8] полагается на стандартную формулу для генерации всех примитивных пифагоровых троек:

${ Displaystyle а = м ^ {2} -n ^ {2}, ,}$

${ displaystyle b = 2mn, ,}$

${ Displaystyle с = м ^ {2} + п ^ {2}, ,}$

с м > п > 0 и м и п взаимно простой и противоположной четности. Пары (м, п) можно повторять путем предварительного умножения их (выраженного как вектор-столбец) на любой из

${ displaystyle { begin {array} {lcr} { begin {bmatrix} 2 & -1 1 & 0 end {bmatrix}}, & { begin {bmatrix} 2 & 1 1 & 0 end {bmatrix}}, & { begin {bmatrix} 1 & 2 0 & 1 end {bmatrix}}, end {array}}}$

каждое из которых сохраняет неравенства, взаимную простоту и противоположную четность. Результирующее тернарное дерево, начиная с (2,1), содержит все такие (м, п) пара ровно один раз, а при преобразовании в (а, б, c) троек, оно становится идентичным описанному выше дереву.

Другой способ использования двух базовых параметров для создания дерева троек^[9] использует альтернативную формулу для всех примитивных троек:

${ Displaystyle а = уф, ,}$

${ displaystyle b = { frac {u ^ {2} -v ^ {2}} {2}},}$

${ displaystyle c = { frac {u ^ {2} + v ^ {2}} {2}},}$

с ты > v > 0 и ты и v coprime и оба странные. Пары (ты, v) можно повторить путем предварительного умножения их (выраженного как вектор-столбец) на любую из указанных выше матриц 2 × 2, все три из которых сохраняют неравенства, взаимную простоту и нечетную четность обоих элементов. Когда этот процесс начинается в (3, 1), результирующее троичное дерево содержит все такие (ты, v) пара ровно один раз, а при преобразовании в (а, б, c) троек, оно становится идентичным описанному выше дереву.

Другое дерево

В качестве альтернативы, можно также использовать 3 разные матрицы, найденные Прайсом.^[6] Эти матрицы А ', Б', В ' и соответствующие им линейные преобразования показаны ниже.

${ Displaystyle { overset {{A} '} { mathop { left [{ begin {matrix} 2 & 1 & -1 - 2 & 2 & 2 - 2 & 1 & 3 end {matrix}} right]}}} left [{ begin {matrix} a b c end {matrix}} right] = left [{ begin {matrix} a_ {1} b_ {1} c_ {1} end {matrix}} right], quad { text {}} { overset {{B} '} { mathop { left [{ begin {matrix}} 2 & 1 & 1 2 & -2 & 2 2 & -1 & 3 end {matrix}} right]}}} left [{ begin {matrix} a b c end {matrix}} right] = left [{ begin {matrix} a_ {2} b_ {2} c_ {2} end {matrix}} right], quad { text {}} { overset {{C} '} { mathop { left [{ begin {matrix} 2 & -1 & 1 2 & 2 & 2 2 & 1 & 3 end {matrix}} right]}}} left [{ begin {matrix} a b c end {матрица }} right] = left [{ begin {matrix} a_ {3} b_ {3} c_ {3} end {matrix}} right]}$

Три линейных преобразования цены:

${ displaystyle { begin {align} & { begin {matrix} + 2a + bc = a_ {1} quad & -2a + 2b + 2c = b_ {1} quad & -2a + b + 3c = c_ {1} & quad to left [{ text {}} a_ {1}, { text {}} b_ {1}, { text {}} c_ {1} right] end {матрица }} & { begin {matrix} + 2a + b + c = a_ {2} quad & + 2a-2b + 2c = b_ {2} quad & + 2a-b + 3c = c_ {2} & quad to left [{ text {}} a_ {2}, { text {}} b_ {2}, { text {}} c_ {2} right] end {matrix}} & { begin {matrix} + 2a-b + c = a_ {3} quad & + 2a + 2b + 2c = b_ {3} quad & + 2a + b + 3c = c_ {3} & quad to left [{ text {}} a_ {3}, { text {}} b_ {3}, { text {}} c_ {3} right] end {matrix}} & конец {выровнен}}}$

Три дочерних элемента, созданные каждым из двух наборов матриц, не совпадают, но каждый набор отдельно создает все примитивные тройки.

Например, используя [5, 12, 13] в качестве родителя, мы получаем два набора из трех дочерних элементов:

${ displaystyle { begin {array} {ccc} & left [5,12,13 right] & A & B & C left [45,28,53 right] & left [55,48,73 right] & left [7,24,25 right] end {array}} quad quad quad quad quad quad { begin {array} {ccc} {} & left [5, 12,13 right] & {} A '& B' & C ' left [9,40,41 right] & left [35,12,37 right] и left [11,60, 61 right] end {array}}}$

Примечания и ссылки

внешняя ссылка

• Тройное дерево (а), лежащее в основе примитивных троек Пифагора в завязать узел
• Франк Р. Бернхарт и Х. Ли Прайс, «Повторное посещение сада Пифагора», Австралийский журнал старших математиков, 01/2012; 26 (1): 29-40.[1]
• Вайсштейн, Эрик В. «Тройной Пифагора». MathWorld.