Допустимое правило - Admissible rule
В логика, а правило вывода является допустимый в формальная система если набор теоремы системы не изменяется, когда это правило добавляется к существующим правилам системы. Другими словами, каждый формула это может быть полученный использование этого правила уже можно вывести без этого правила, поэтому в некотором смысле оно избыточно. Понятие допустимого правила было введено Пол Лоренцен (1955).
Определения
Допустимость систематически изучалась только в случае структурных правил в пропозициональный неклассическая логика, о котором мы расскажем далее.
Пусть набор основных пропозициональные связки быть фиксированным (например, в случае суперинтуиционистская логика, или же в случае мономодальные логики ). Правильные формулы строятся свободно, используя эти связки из счетно бесконечный набор из пропозициональные переменные п0, п1, .... А замена σ - это функция от формул к формулам, которая коммутирует со связками, т. е.
для каждого связующего ж, и формулы А1, ..., Ап. (Мы также можем применять замены к множествам формул Γ, делая σΓ = {σА: А ∈ Γ}.) В стиле Тарского отношение последствий[1] это отношение между наборами формул и формулами, такими, что
- если тогда
- если и тогда
для всех формул А, B, и множества формул Γ, ∆. Отношение следствия такое, что
- если тогда
для всех замен σ называется структурный. (Обратите внимание, что термин «структурный», используемый здесь и ниже, не имеет отношения к понятию структурные правила в последовательные исчисления.) Отношение структурного следствия называется логика высказываний. Формула А это теорема логики если .
Например, мы идентифицируем суперинтуиционистскую логику L со стандартным отношением следствия аксиоматизируемый modus ponens и аксиомы, и мы идентифицируем нормальная модальная логика с его отношением глобального следствия аксиоматизируется modus ponens, необходимостью и аксиомами.
А правило структурного вывода[2] (или просто правило для краткости) задается парой (Γ,B), обычно записываемый как
где Γ = {А1, ..., Ап} - конечный набор формул, а B это формула. An пример правила
для замены σ. Правило Γ /B является выводимый в , если . это допустимый если для каждого случая правила σB является теоремой, если все формулы из σΓ являются теоремами.[3] Другими словами, правило допустимо, если, будучи добавленным к логике, не приводит к новым теоремам.[4] Мы также пишем если Γ /B допустимо. (Обратите внимание, что является структурным отношением следствия само по себе.)
Любое выводимое правило допустимо, но не наоборот. Логика структурно завершенный если каждое допустимое правило выводимо, т. е. .[5]
По логике с хорошо себя соединение связка (например, суперинтуиционистская или модальная логика), правило эквивалентно относительно допустимости и выводимости. Поэтому принято иметь дело только с унарный правила А/B.
Примеры
- Классическое исчисление высказываний (Цена за клик) конструктивно завершена.[6] Действительно, предположим, что А/B невыводимое правило, и исправить присвоение v такой, что v(А) = 1 и v(B) = 0. Определим такую замену σ, чтобы для каждой переменной п, σп = если v(п) = 1 и σп = если v(п) = 0. Тогда σА это теорема, но σB не является (на самом деле ¬σB это теорема). Таким образом, правило А/B тоже не допускается. (Тот же аргумент применим к любому многозначная логика L завершена по отношению к логической матрице, все элементы которой имеют имя на языке L.)
- В Kreisel –Putnam правило (a.k.a. Харроп правило или независимость от правила посылок)
- допустимо в интуиционистское исчисление высказываний (МПК). Фактически, это допустимо в любой суперинтуиционистской логике.[7] С другой стороны, формула
- не является интуиционистской тавтологией, поэтому КПР не выводится в МПК. Особенно, МПК структурно не завершена.
- Правило
- допустимо во многих модальных логиках, таких как K, D, K4, S4, GL (видеть этот стол для имен модальных логик). Это выводится в S4, но не выводится в K, D, K4, или GL.
- Правило
- допустима в любой нормальной модальной логике.[8] Это выводится в GL и S4.1, но не выводится в K, D, K4, S4, S5.
- допустима (но не выводима) в основной модальной логике K, и он выводится в GL. Тем не мение, LR не допускается в K4. В частности, это нет правда в общем, что правило, допустимое в логике L должны быть допустимы в своих расширениях.
- В Логика Гёделя – Даммета (LC), а модальная логика Grz.3 конструктивно завершены.[9] В нечеткая логика продукта также конструктивно завершена.[10]
Разрешимость и сокращенные правила
Основной вопрос о допустимых правилах данной логики состоит в том, является ли набор всех допустимых правил разрешимый. Обратите внимание, что проблема нетривиальна, даже если сама логика (то есть ее набор теорем) разрешимый: определение допустимости правила А/B включает в себя неограниченный универсальный квантор по всем пропозициональным заменам, поэтому априори мы знаем только, что допустимость правила в разрешимой логике (т.е. его дополнение рекурсивно перечислимый ). Например, известно, что допустимость в бимодальной логике Kты и K4ты (расширение K или же K4 с универсальная модальность ) неразрешима.[11] Примечательно, что разрешимость допустимости в базовой модальной логике K это большая открытая проблема.
Тем не менее, как известно, допустимость правил разрешима во многих модальных и суперинтуиционистских логиках. Первые решающие процедуры для допустимых правил в основных транзитивных модальных логиках были построены Рыбаков, с использованием сокращенная форма правил.[12] Модальное правило в переменных п0, ..., пk называется приведенным, если он имеет вид
где каждый либо пусто, либо отрицание . Для каждого правила р, мы можем эффективно построить сокращенное правило s (называется сокращенной формой р) такая, что любая логика допускает (или выводит) р тогда и только тогда, когда он допускает (или выводит) s, введя переменные расширения для всех подформул в А, и выражая результат в полной дизъюнктивная нормальная форма. Таким образом, достаточно построить алгоритм принятия решения о допустимости редуцированных правил.
Позволять быть сокращенным правилом, как указано выше. Мы идентифицируем каждое соединение с набором его конъюнктов. Для любого подмножества W из набора всех союзов, определим Модель Крипке к
Далее приводится алгоритмический критерий допустимости в K4:[13]
Теорема. Правило является нет допустимый в K4 тогда и только тогда, когда существует множество такой, что
- для некоторых
- для каждого
- для каждого подмножества D из W есть элементы такие, что эквивалентности
- если и только если для каждого
- если и только если и для каждого
- держать для всех j.
Аналогичные критерии можно найти и для логики S4, GL, и Grz.[14] Более того, допустимость в интуиционистской логике может быть сведена к допустимости в Grz с использованием Перевод Геделя – МакКинси – Тарского:[15]
- если и только если
Рыбаков (1997) разработал гораздо более сложные методы для демонстрации разрешимости допустимости, которые применимы к робастному (бесконечному) классу транзитивных (т.е. K4 или МПК) модальные и суперинтуиционистские логики, включая, например, S4.1, S4.2, S4.3, KC, Тk (а также упомянутую выше логику МПК, K4, S4, GL, Grz).[16]
Несмотря на свою разрешимость, проблема допустимости имеет относительно высокий уровень вычислительная сложность, даже в простых логиках: допустимость правил в основных транзитивных логиках МПК, K4, S4, GL, Grz является coNEXP -полный.[17] Это должно контрастировать с проблемой выводимости (для правил или формул) в этих логиках, которая PSPACE -полный.[18]
Проективность и унификация
Допустимость в логике высказываний тесно связана с объединением в эквациональная теория из модальный или же Гейтинговые алгебры. Связь была разработана Ghilardi (1999, 2000). В логической настройке объединитель формулы А в логике L (ан L-unifier для краткости) - такая подстановка σ, что σА это теорема L. (Используя это понятие, мы можем перефразировать допустимость правила А/B в L как "каждый L-объединитель А является L-объединитель B".) L-унификатор σ является менее общий чем L-объединитель τ, записываемый как σ ≤ τ, если существует такая подстановка υ, что
для каждой переменной п. А полный комплект унификаторов формулы А это набор S из L-унификаторы А так что каждый L- объединитель А менее общий, чем некоторый объединитель из S. А самый общий объединитель (mgu) из А - объединитель σ такой, что {σ} - полный набор объединителей А. Отсюда следует, что если S полный набор унификаторов А, тогда правило А/B является L-допустимым тогда и только тогда, когда каждое σ из S является L-объединитель B. Таким образом, мы можем охарактеризовать допустимые правила, если сможем найти хорошо работающие полные наборы унификаторов.
Важным классом формул, имеющих самый общий объединитель, являются проективные формулы: это формулы А такой, что существует объединитель σ А такой, что
для каждой формулы B. Обратите внимание, что σ является mgu А. В транзитивных модальных и суперинтуиционистских логиках с конечное свойство модели (fmp), можно семантически характеризовать проективные формулы как те, у которых множество конечных L-модели имеют свойство расширения:[19] если M конечный Крипке L-модель с рутом р чей кластер одиночка, а формула А выполняется во всех точках M кроме р, то мы можем изменить оценку переменных в р чтобы сделать А правда в р также. Более того, доказательство дает явную конструкцию mgu для данной проективной формулы А.
В основных транзитивных логиках МПК, K4, S4, GL, Grz (и, в более общем смысле, в любой транзитивной логике с fmp, чей набор конечных фреймов удовлетворяет другому виду свойства расширения), мы можем эффективно построить для любой формулы А это проективное приближение Π (А):[20] конечный набор проективных формул таких, что
- для каждого
- каждый объединитель А является объединителем формулы из Π (А).
Отсюда следует, что множество элементов множества of (А) представляет собой полный набор объединителей А. Кроме того, если п - проективная формула, то
- если и только если
для любой формулы B. Таким образом, мы получаем следующую эффективную характеристику допустимых правил:[21]
- если и только если
Основы допустимых правил
Позволять L быть логикой. Множество р из L-допустимое правило называется основа[22] допустимых правил, если каждое допустимое правило Γ /B может быть получено из р и выводимые правила L, используя замещение, композицию и ослабление. Другими словами, р является базисом тогда и только тогда, когда наименьшее отношение структурных последствий, которое включает и р.
Обратите внимание, что разрешимость допустимых правил разрешимой логики эквивалентна существованию рекурсивного (или рекурсивно перечислимый ) баз: с одной стороны, набор все допустимое правило является рекурсивным основанием, если допустимость разрешима. С другой стороны, набор допустимых правил всегда сопряжен, и если в дальнейшем у нас есть случайный набор правил. базис, он также r.e., следовательно, разрешим. (Другими словами, мы можем решить допустимость А/B следующими алгоритм: запускаем параллельно два исчерпывающий поиск, один для замены σ, объединяющей А но нет B, и один для вывода А/B из р и . Один из поисков должен в конечном итоге дать ответ.) Помимо разрешимости, явные основы допустимых правил полезны для некоторых приложений, например в сложность доказательства.[23]
Для данной логики мы можем спросить, имеет ли она рекурсивную или конечный основы допустимых правил и предоставить явную основу. Если у логики нет конечной основы, она, тем не менее, может иметь независимая основа: основа р такой, что нет подходящего подмножества р это основа.
В общем, о существовании баз с желаемыми свойствами можно сказать очень мало. Например, пока табличная логика обычно хорошо себя ведут и всегда конечно аксиоматизируемы, существуют табличные модальные логики без конечного или независимого базиса правил.[24] Конечные базисы относительно редки: даже базовые транзитивные логики МПК, K4, S4, GL, Grz не имеют конечного базиса допустимых правил,[25] хотя у них есть независимые базы.[26]
Примеры баз
- Пустой набор - основа L-допустимые правила тогда и только тогда, когда L конструктивно завершена.
- Каждое расширение модальной логики S4.3 (включая, в частности, S5) имеет конечный базис, состоящий из единственного правила[27]
- Visser правила
- являются основой допустимых правил в МПК или же KC.[28]
- Правила
- являются основой допустимых правил GL.[29] (Обратите внимание, что пустая дизъюнкция определяется как .)
- Правила
- являются основой допустимых правил S4 или Grz.[30]
Семантика допустимых правил
Правило Γ /B является действительный в модальном или интуиционистском Рамка Крипке , если для каждой оценки верно следующее в F:
- если для всех , тогда .
(Определение легко обобщается на общие рамки, если нужно.)
Позволять Икс быть подмножеством W, и т точка в W. Мы говорим что т является
- а рефлексивный жесткий предшественник из Икс, если для каждого у в W: пытаться если и только если т = у или же Икс = у или же x R y для некоторых Икс в Икс,
- ан иррефлексивный жесткий предшественник из Икс, если для каждого у в W: пытаться если и только если Икс = у или же x R y для некоторых Икс в Икс.
Мы говорим, что рамка F имеет рефлексивных (иррефлексивных) тугих предшественников, если для каждого конечный подмножество Икс из W, существует рефлексивный (иррефлексивный) плотный предшественник Икс в W.
У нас есть:[31]
- правило допустимо в МПК тогда и только тогда, когда это верно во всех интуиционистских рамках, которые имеют рефлексивных плотных предшественников
- правило допустимо в K4 тогда и только тогда, когда оно действительно во всех переходный кадры, у которых есть возвратные и нерефлексивные плотные предшественники,
- правило допустимо в S4 тогда и только тогда, когда это верно во всех транзитивных рефлексивный рамы, у которых есть возвратные тугие предшественники,
- правило допустимо в GL тогда и только тогда, когда это верно во всех транзитивных обратных обоснованный кадры, у которых есть иррефлексивные жесткие предшественники.
Обратите внимание, что за исключением нескольких тривиальных случаев, фреймы с точными предшественниками должны быть бесконечными, следовательно, допустимые правила в базовой транзитивной логике не обладают свойством конечной модели.
Структурная завершенность
Хотя общая классификация структурно полных логик - непростая задача, мы хорошо разбираемся в некоторых частных случаях.
Сама интуиционистская логика структурно не завершена, но ее фрагменты может вести себя по-другому. А именно, любое правило без дизъюнкции или правило без импликации, допустимое в суперинтуиционистской логике, выводимо.[32] С другой стороны, правило монетного двора
допустима в интуиционистской логике, но не выводима и содержит только импликации и дизъюнкции.
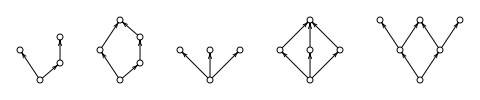
Мы знаем максимальный структурно неполная транзитивная логика. Логика называется наследственно структурно полный, если какое-либо пристройка завершена конструктивно. Например, классическая логика, а также логика LC и Grz.3, упомянутые выше, являются наследственно структурно законченными. Полное описание наследственно структурно полной суперинтуиционистской и транзитивной модальных логик было дано соответственно Циткиным и Рыбаковым. А именно, суперинтуиционистская логика наследственно структурно завершена тогда и только тогда, когда она не верна ни в одной из пяти фреймов Крипке.[9]
Точно так же расширение K4 является наследственно структурно завершенным тогда и только тогда, когда он не действителен ни в одной из определенных двадцати систем Крипке (включая пять интуиционистских рамок выше).[9]
Существуют структурно завершенные логики, которые не являются наследственно структурно завершенными: например, Логика Медведева конструктивно завершена,[33] но это входит в структурно неполную логику KC.
Варианты
А правило с параметрами это правило формы
переменные которого делятся на «обычные» переменные пя, а параметры sя. Правило L-допустимым, если каждые L-объединитель σ А такое, что σsя = sя для каждого я также объединяет B. Основные результаты разрешимости допустимых правил также относятся к правилам с параметрами.[34]
А правило множественного заключения представляет собой пару (Γ, Δ) двух конечных наборов формул, записанных как
Такое правило допустимо, если каждый объединитель Γ также является объединителем некоторой формулы из Δ.[35] Например, логика L является последовательный если и если он допускает правило
и суперинтуиционистская логика имеет дизъюнктивное свойство если и если он допускает правило
Опять же, основные результаты о допустимых правилах плавно обобщаются на правила с несколькими выводами.[36] В логиках с вариантом свойства дизъюнкции правила множественного заключения имеют такую же выразительную силу, что и правила одиночного заключения: например, в S4 приведенное выше правило эквивалентно
Тем не менее, правила множественного вывода часто можно использовать для упрощения аргументов.
В теория доказательств, приемлемость часто рассматривается в контексте последовательные исчисления, где базовыми объектами являются секвенции, а не формулы. Например, можно перефразировать теорема исключения сечения как утверждая, что исчисление секвенций допускает вырезать правило
(Злоупотребляя языком, также иногда говорят, что (полное) исчисление секвенций допускает отсечение, что означает, что его версия без отсечений допускает.) Однако допустимость в исчислениях секвенций обычно является лишь вариантом обозначения допустимости в соответствующей логике: любая полное исчисление (скажем) интуиционистской логики допускает правило секвенции тогда и только тогда, когда МПК допускает правило формулы, которое мы получаем, переводя каждую секвенцию к его характерной формуле .
Примечания
- ^ Блок и Пигоцци (1989), Крахт (2007)
- ^ Рыбаков (1997), Защ. 1.1.3
- ^ Рыбаков (1997), Защ. 1.7.2
- ^ От теоремы де Йонга к интуиционистской логике доказательств
- ^ Рыбаков (1997), Защ. 1.7.7
- ^ Чагров и Захарьящев (1997), Thm. 1,25
- ^ Prucnal (1979), ср. Имхофф (2006)
- ^ Рыбаков (1997), с. 439
- ^ а б c Рыбаков (1997), Thms. 5.4.4, 5.4.8
- ^ Синтула и Меткалф (2009)
- ^ Вольтер и Захарьящев (2008)
- ^ Рыбаков (1997), §3.9
- ^ Рыбаков (1997), Thm. 3.9.3
- ^ Рыбаков (1997), Thms. 3.9.6, 3.9.9, 3.9.12; ср. Чагров и Захарьящев (1997), §16.7
- ^ Рыбаков (1997), Thm. 3.2.2
- ^ Рыбаков (1997), §3.5
- ^ Ержабек (2007)
- ^ Чагров и Захарящев (1997), §18.5
- ^ Гиларди (2000), Thm. 2.2
- ^ Гиларди (2000), стр. 196
- ^ Гиларди (2000), Thm. 3,6
- ^ Рыбаков (1997), Защ. 1.4.13
- ^ Минц и Кожевников (2004)
- ^ Рыбаков (1997), Thm. 4.5.5
- ^ Рыбаков (1997), §4.2
- ^ Ержабек (2008)
- ^ Рыбаков (1997), Кор. 4.3.20
- ^ Иемхофф (2001, 2005), Розьер (1992)
- ^ Ержабек (2005)
- ^ Ержабек (2005,2008)
- ^ Иемхофф (2001), Ержабек (2005)
- ^ Рыбаков (1997), Thms. 5.5.6, 5.5.9
- ^ Прукнал (1976)
- ^ Рыбаков (1997), §6.1
- ^ Ержабек (2005); ср. Крахт (2007), §7
- ^ Ержабек (2005, 2007, 2008)
Рекомендации
- В. Блок, Д. Пигоцци, Алгебраизируемые логики, Мемуары Американского математического общества 77 (1989), вып. 396, 1989 г.
- А. Чагров и М. Захарящев, Модальная логика, Oxford Logic Guides, т. 35, Oxford University Press, 1997. ISBN 0-19-853779-4
- П. Синтула и Г. Меткалф, Структурная полнота в нечеткой логике, Notre Dame Journal of Formal Logic 50 (2009), нет. 2. С. 153–182. Дои:10.1215/00294527-2009-004
- Циткин А.И., О структурно полной суперинтуиционистской логике// Советская математика. - Докл. 19 (1978), стр. 816–819.
- С. Гиларди, Объединение в интуиционистской логике, Журнал символической логики 64 (1999), вып. 2. С. 859–880. Проект Евклид JSTOR
- С. Гиларди, Лучшее решение модальных уравнений, Анналы чистой и прикладной логики 102 (2000), вып. 3. С. 183–198. Дои:10.1016 / S0168-0072 (99) 00032-9
- Р. Иемхофф, О допустимых правилах интуиционистской логики высказываний, Журнал символической логики 66 (2001), нет. 1. С. 281–294. Проект Евклид JSTOR
- Р. Иемхофф, Промежуточная логика и правила Виссера, Журнал формальной логики Нотр-Дам 46 (2005), нет. 1. С. 65–81. Дои:10.1305 / ndjfl / 1107220674
- Р. Иемхофф, О правилах промежуточной логики, Архив математической логики, 45 (2006), вып. 5. С. 581–599. Дои:10.1007 / s00153-006-0320-8
- Э. Ержабек, Допустимые правила модальных логик, Журнал логики и вычислений 15 (2005), вып. 4. С. 411–431. Дои:10.1093 / logcom / exi029
- Э. Ержабек, Сложность допустимых правил, Архив математической логики 46 (2007), вып. 2. С. 73–92. Дои:10.1007 / s00153-006-0028-9
- Э. Ержабек, Независимые основы допустимых правил, Логический журнал IGPL 16 (2008), вып. 3. С. 249–267. Дои:10.1093 / jigpal / jzn004
- М. Крахт, Модальные отношения последствий, в: Справочник по модальной логике (П. Блэкберн, Дж. ван Бентем и Ф. Вольтер, ред.), Исследования логики и практического мышления, том. 3, Elsevier, 2007, стр. 492–545. ISBN 978-0-444-51690-9
- П. Лоренцен, Einführung в оперативной Logik und Mathematik, Grundlehren der Mathematischen Wissenschaften vol. 78, Springer – Verlag, 1955.
- Г. Минц и А. Кожевников, Интуиционистские системы Фреге полиномиально эквивалентны// Записки научных семинаров ПОМИ 316 (2004). С. 129–146. gzip PS
- Т. Прукнал, Структурная полнота исчисления высказываний Медведева, Reports on Mathematical Logic 6 (1976), pp. 103–105.
- Т. Прукнал, О двух проблемах Харви Фридмана, Studia Logica 38 (1979), нет. 3. С. 247–262. Дои:10.1007 / BF00405383
- П. Розьер, Règles допустимых en Calculate propositionnel intuitionniste, Кандидат наук. диссертация, Парижский университет VII, 1992. PDF
- Рыбаков В.В., Допустимость правил логического вывода, Исследования по логике и основам математики т. 136, Elsevier, 1997. ISBN 0-444-89505-1
- Ф. Вольтер, М. Захарящев, Неразрешимость проблем унификации и допустимости модальных и описательных логик, Транзакции ACM по вычислительной логике 9 (2008), вып. 4, статья № 25. Дои:10.1145/1380572.1380574 PDF