Дерево двоичных выражений - Binary expression tree

А дерево двоичных выражений это особый вид двоичное дерево используется для представления выражения. Двумя распространенными типами выражений, которые может представлять дерево двоичных выражений, являются: алгебраический^[1] и логический. Эти деревья могут представлять выражения, содержащие как унарный и двоичный операторы.^[1]

Каждый узел двоичного дерева и, следовательно, дерева двоичного выражения имеет ноль, одного или двух дочерних элементов. Эта ограниченная структура упрощает обработку деревьев выражений.

Обзор

Дерево выражений выражения (a + b) * c + 7

Листья дерева двоичных выражений - это операнды, такие как константы или имена переменных, а другие узлы содержат операторы. Эти конкретные деревья оказываются двоичными, потому что все операции являются двоичными, и, хотя это самый простой случай, у узлов может быть более двух дочерних элементов. Также возможно, что у узла будет только один дочерний элемент, как в случае с унарным оператором минус. Дерево выражений, Т, можно оценить, применив оператор в корне к значениям, полученным рекурсивным вычислением левого и правого поддеревьев.^[2]

Обход

Алгебраическое выражение может быть получено из дерева двоичных выражений путем рекурсивного создания заключенного в скобки левого выражения, затем распечатки оператора в корне и, наконец, рекурсивного создания заключенного в скобки правого выражения. Эта общая стратегия (слева, узел, справа) известна как обход по порядку Альтернативная стратегия обхода - рекурсивно распечатать левое поддерево, правое поддерево и затем оператор. Эта стратегия обхода обычно известна как обход после заказа. Третья стратегия - сначала распечатать оператор, а затем рекурсивно распечатать левое и правое поддерево, известное как обход предварительного заказа.^[2]

Эти три стандартных обхода в глубину представляют три разных формата выражений: инфиксный, постфиксный и префиксный. Инфиксное выражение создается обходом в порядке, постфиксное выражение создается обходом после порядка, а префиксное выражение создается обходом перед порядком.^[3]

Обход инфиксов

Когда печатается инфиксное выражение, открывающая и закрывающая круглые скобки должны быть добавлены в начале и в конце каждого выражения. Поскольку каждое поддерево представляет собой подвыражение, открывающая скобка печатается в его начале, а закрывающая скобка печатается после обработки всех его дочерних элементов.

Псевдокод:

Алгоритм инфикс (дерево)/ * Вывести инфиксное выражение для дерева выражения. Pre: tree - это указатель на дерево выражения Сообщение: напечатано инфиксное выражение * / если (дерево нет пустой)    если (дерево жетон является оператор)       Распечатать (открыто скобка)    конец если    инфикс (дерево оставили поддерево)    Распечатать (дерево жетон)    инфикс (дерево верно поддерево)    если (дерево жетон является оператор)       Распечатать (Закрыть скобка)    конец если конец есликонец инфикс

Постфиксный обход

В постфикс Выражение формируется в результате базового обхода любого двоичного дерева после упорядочения. Скобки не требуются.

Псевдокод:

Алгоритм постфикс (дерево)/ * Вывести постфиксное выражение для дерева выражения. Pre: tree - это указатель на дерево выражения Сообщение: напечатано постфиксное выражение * / если (дерево нет пустой)    постфикс (дерево оставили поддерево)    постфикс (дерево верно поддерево)    Распечатать (дерево жетон) конец есликонец постфикс

Префиксный обход

Псевдокод:

Алгоритм префикс (дерево)/ * Вывести префиксное выражение для дерева выражения. Pre: tree - это указатель на дерево выражения Сообщение: напечатано префиксное выражение * / если (дерево нет пустой)    Распечатать (дерево жетон)    префикс (дерево оставили поддерево)    префикс (дерево верно поддерево) конец есликонец префикс

Построение дерева выражений

Построение дерева происходит путем чтения постфиксного выражения по одному символу за раз. Если символ является операндом, создается одноузловое дерево, и его указатель помещается на куча. Если символ является оператором, указатели на два дерева Т1 и Т2 извлекаются из стека, и новое дерево, корнем которого является оператор, а левый и правый дочерние элементы которого указывают на Т2 и Т1 соответственно формируется. Затем указатель на это новое дерево помещается в стек.^[4]

Пример

Ввод в постфиксной нотации: a b + c d e + * * Поскольку первые два символа являются операндами, создаются одноузловые деревья и указатели на них помещаются в стек. Для удобства стек будет расти слева направо.

Стек растет слева направо

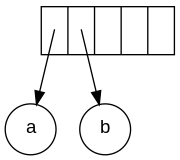
Следующий символ - "+". Он выталкивает два указателя на деревья, формируется новое дерево, и указатель на него помещается в стек.

Формирование нового дерева

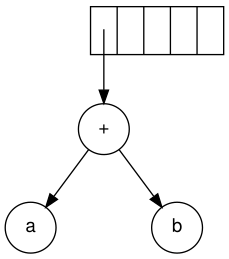
Затем считываются c, d и e. Для каждого создается одноузловое дерево, и указатель на соответствующее дерево помещается в стек.

Создание одноузлового дерева

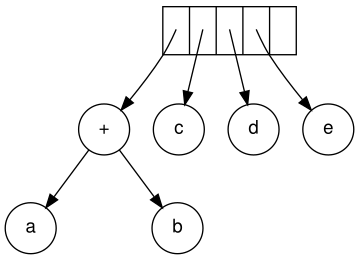
Далее читается знак «+», и последние два дерева объединяются.

Слияние двух деревьев

Теперь читается "*". Выскакивают два последних указателя на дерево, и формируется новое дерево со знаком «*» в качестве корня.

Формирование нового дерева с корнем

Наконец, читается последний символ. Два дерева объединяются, и указатель на последнее дерево остается в стеке.^[5]

Шаги по построению дерева выражений a b + c d e + * *

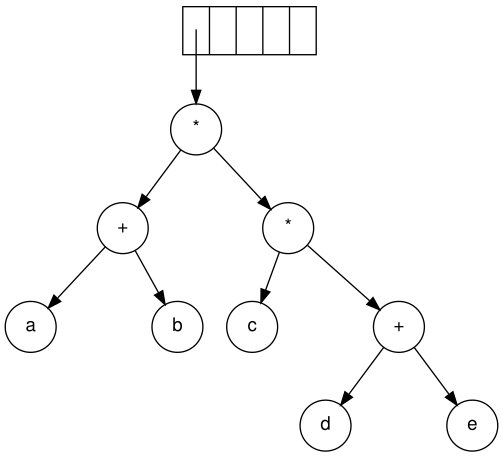
Алгебраические выражения

Дерево двоичных алгебраических выражений, эквивалентное ((5 + z) / -8) * (4 ^ 2)

Деревья алгебраических выражений представляют собой выражения, содержащие числа, переменные, а также унарные и бинарные операторы. Некоторые из общих операторов: × (умножение ), ÷ (разделение ), + (добавление ), − (вычитание ), ^ (возведение в степень ), и - (отрицание ). Операторы содержатся в внутренние узлы дерева, с числами и переменными в листовые узлы.^[1] Узлы бинарных операторов имеют два дочерние узлы, а у унарных операторов есть один дочерний узел.

Логические выражения

Дерево двоичного логического выражения, эквивалентное ((true ${ displaystyle lor}$ ложный) ${ displaystyle land}$ ${ displaystyle neg}$ложный) ${ displaystyle lor}$ (истинный ${ displaystyle lor}$ ложный))

Булевы выражения представлены очень аналогично алгебраическим выражениям, с той лишь разницей, что используются конкретные значения и операторы. Использование логических выражений истинный и ложный как постоянные значения, а операторы включают ${ displaystyle land}$ (И ), ${ displaystyle lor}$ (ИЛИ ЖЕ ), ${ displaystyle neg}$ (НЕТ ).

Смотрите также

• Выражение (математика)
• Срок (логика)
• Бесконтекстная грамматика
• Дерево синтаксического анализа
• Абстрактное синтаксическое дерево

Рекомендации