Пограничный слой - Boundary layer

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: "Пограничный слой"  – Новости  · газеты  · книги  · ученый  · JSTOR (Март 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

В физика и механика жидкости, а пограничный слой слой жидкость в непосредственной близости от ограничивающая поверхность где влияние вязкости значимо.

в Атмосфера Земли, то пограничный слой атмосферы воздушный слой у земли, подверженный влиянию дневная жара передача влаги или количества движения к поверхности или от поверхности. На самолет крыло пограничный слой - это часть потока, близкая к крылу, где вязкий силы искажать окружающий невязкий поток.

Типы пограничного слоя

Визуализация пограничного слоя, показывающая переход от ламинарного к турбулентному состоянию

Ламинарные пограничные слои можно условно классифицировать в соответствии с их структурой и условиями, в которых они созданы. Тонкий слой сдвига, который образуется на колеблющемся теле, является примером Пограничный слой Стокса, в то время как Пограничный слой Блазиуса относится к хорошо известным сходство раствор рядом с прикрепленной плоской пластиной, удерживаемый встречным однонаправленным потоком и Пограничный слой Фолкнера – Скан, обобщение профиля Блазиуса. Когда жидкость вращается и силы вязкости уравновешиваются Эффект Кориолиса (а не конвективная инерция), Слой Экмана формы. В теории теплопередачи возникает тепловой пограничный слой. Поверхность может иметь одновременно несколько типов пограничного слоя.

Вязкий характер воздушного потока снижает локальные скорости на поверхности и вызывает трение кожи. Слой воздуха над поверхностью крыла, который замедляется или останавливается из-за вязкости, является пограничным слоем. Существует два различных типа течения в пограничном слое: ламинарный и турбулентный.^[1]

Ламинарное течение в пограничном слое

Ламинарная граница представляет собой очень плавное течение, а турбулентный пограничный слой содержит завихрения или «водовороты». Ламинарный поток создает меньшее сопротивление поверхностного трения, чем турбулентный поток, но менее стабилен. Течение пограничного слоя по поверхности крыла начинается как плавное ламинарное течение. По мере того как поток продолжается обратно от передней кромки, толщина ламинарного пограничного слоя увеличивается.

Турбулентный поток в пограничном слое

На некотором удалении от передней кромки плавный ламинарный поток прерывается и переходит в турбулентный поток. С точки зрения лобового сопротивления, желательно иметь переход от ламинарного к турбулентному потоку как можно дальше от кормы крыла или иметь большую площадь поверхности крыла в ламинарной части пограничного слоя. Однако ламинарный поток с низкой энергией имеет тенденцию к более резкому разрушению, чем турбулентный слой.

Аэродинамика

Людвиг Прандтль

Профиль скорости ламинарного пограничного слоя

В аэродинамический пограничный слой был впервые определен Людвиг Прандтль в статье, представленной 12 августа 1904 г. на третьем Международный конгресс математиков в Гейдельберг, Германия. Он упрощает уравнения потока жидкости, разделяя поле потока на две области: одна внутри пограничного слоя, в которой преобладают вязкость и создание большинства тащить испытанный пограничным телом; и один за пределами пограничного слоя, где вязкостью можно пренебречь без значительного влияния на раствор. Это позволяет закрытое решение для потока в обеих областях, значительное упрощение полного Уравнения Навье – Стокса. Большинство теплопередача к телу и от тела также происходит внутри пограничного слоя, что снова позволяет упростить уравнения в поле потока за пределами пограничного слоя. Распределение давления в пограничном слое в направлении, нормальном к поверхности (например, профиль ) остается постоянным во всем пограничном слое и остается таким же, как и на самой поверхности.

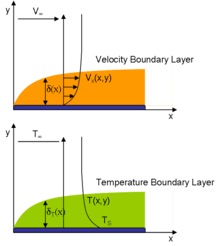
В толщина Граничный слой скорости обычно определяется как расстояние от твердого тела до точки, в которой скорость вязкого потока составляет 99% скорости набегающего потока (поверхностная скорость невязкого потока).^{[нужна цитата ]} Толщина смещения - альтернативное определение, в котором говорится, что пограничный слой представляет собой дефицит массового расхода по сравнению с невязким потоком со скольжением на стенке. Это расстояние, на которое стенка должна быть смещена в невязком случае, чтобы получить такой же общий массовый расход, как и в вязком случае. В условие противоскольжения требует, чтобы скорость потока на поверхности твердого объекта была равна нулю, а температура жидкости была равна температуре поверхности. Затем скорость потока в пограничном слое будет быстро увеличиваться в соответствии с приведенными ниже уравнениями пограничного слоя.

В толщина теплового пограничного слоя аналогично расстояние от тела, на котором температура составляет 99% от температуры набегающего потока. Соотношение двух толщин регулируется Число Прандтля. Если число Прандтля равно 1, два пограничных слоя имеют одинаковую толщину. Если число Прандтля больше 1, тепловой пограничный слой тоньше, чем скоростной пограничный слой. Если число Прандтля меньше 1, что имеет место для воздуха при стандартных условиях, тепловой пограничный слой толще, чем скоростной пограничный слой.

В высокопроизводительных конструкциях, таких как планеры и коммерческие самолеты, большое внимание уделяется управлению поведением пограничного слоя для минимизации сопротивления. Следует учитывать два эффекта. Во-первых, пограничный слой увеличивает эффективную толщину тела за счет толщина вытеснения, следовательно, увеличивая сопротивление давления. Во-вторых, срезать силы на поверхности крыла создают сопротивление трением кожи.

На высоком Числа Рейнольдса, характерных для полноразмерных самолетов, желательно иметь ламинарный пограничный слой. Это приводит к более низкому поверхностному трению из-за характерного профиля скорости ламинарного потока. Однако пограничный слой неизбежно утолщается и становится менее устойчивым по мере того, как поток развивается вдоль тела, и в конечном итоге становится бурный, процесс, известный как переход пограничного слоя. Один из способов решения этой проблемы - отсосать пограничный слой через пористый поверхность (см. Отсос пограничного слоя ). Это может уменьшить сопротивление, но обычно это непрактично из-за его механической сложности и мощности, необходимой для перемещения воздуха и его удаления. Естественный ламинарный поток (NLF) методы сдвигают переход пограничного слоя назад, изменяя форму аэродинамического профиля или фюзеляж так что его самая толстая часть находится ближе к корме и менее толстая. Это снижает скорости в ведущей части, и такое же число Рейнольдса достигается с большей длиной.

На более низком Числа Рейнольдса Как и в случае с моделями самолетов, относительно легко поддерживать ламинарный поток. Это дает низкое трение кожи, что желательно. Однако тот же профиль скорости, который придает ламинарному пограничному слою низкое поверхностное трение, также вызывает сильное влияние на него неблагоприятные градиенты давления. Когда давление в задней части хорды крыла начинает восстанавливаться, ламинарный пограничный слой будет стремиться отделиться от поверхности. Такой разделение потока вызывает большое увеличение сопротивление давления, поскольку значительно увеличивает эффективный размер сечения крыла. В этих случаях может быть выгодно преднамеренно вызвать турбулентность пограничного слоя в точке, предшествующей месту ламинарного разделения, с использованием турбулятор. Более полный профиль скорости турбулентного пограничного слоя позволяет ему выдерживать неблагоприятный градиент давления без разделения. Таким образом, хотя поверхностное трение увеличивается, общее сопротивление уменьшается. Это принцип, по которому ямочки на мячах для гольфа, а также генераторы вихрей на самолете. Также были разработаны специальные секции крыла, которые адаптируют восстановление давления, поэтому ламинарное разделение уменьшается или даже устраняется. Это представляет собой оптимальный компромисс между сопротивлением давления от разделения потока и поверхностным трением от индуцированной турбулентности.

При использовании полумоделей в аэродинамических трубах пениш иногда используется для уменьшения или устранения эффекта пограничного слоя.

Уравнения пограничного слоя

Вычет уравнения пограничного слоя был одним из самых важных достижений в гидродинамике. Используя анализ по порядку величины, известные правящие Уравнения Навье – Стокса из вязкий жидкость течение может быть значительно упрощено в пограничном слое. Примечательно, что характеристика из уравнения в частных производных (PDE) становится параболической, а не эллиптической формой полного уравнения Навье – Стокса. Это значительно упрощает решение уравнений. Используя приближение пограничного слоя, поток делится на невязкую часть (которую легко решить несколькими методами) и пограничный слой, который регулируется более простой задачей PDE. Уравнения неразрывности и Навье – Стокса для двумерной стационарной несжимаемый поток в Декартовы координаты даны

${ displaystyle { partial u over partial x} + { partial upsilon over partial y} = 0}$

${ displaystyle u { partial u over partial x} + upsilon { partial u over partial y} = - {1 over rho} { partial p over partial x} + { nu } left ({ partial ^ {2} u over partial x ^ {2}} + { partial ^ {2} u over partial y ^ {2}} right)}$

${ Displaystyle и { partial upsilon over partial x} + upsilon { partial upsilon over partial y} = - {1 over rho} { partial p over partial y} + { nu} left ({ partial ^ {2} upsilon over partial x ^ {2}} + { partial ^ {2} upsilon over partial y ^ {2}} right)}$

куда ${ displaystyle u}$ и ${ displaystyle upsilon}$ компоненты скорости, ${ displaystyle rho}$ это плотность, ${ displaystyle p}$ давление, а ${ displaystyle nu}$ это кинематическая вязкость жидкости в точке.

Приближение утверждает, что при достаточно высоком Число Рейнольдса течение по поверхности можно разделить на внешнюю область невязкого потока, на которую не влияет вязкость (большая часть потока), и область вблизи поверхности, где важна вязкость (пограничный слой). Позволять ${ displaystyle u}$ и ${ displaystyle upsilon}$ - продольная и поперечная (нормаль к стенке) скорости внутри пограничного слоя соответственно. С помощью масштабный анализ, можно показать, что приведенные выше уравнения движения сводятся в пограничном слое к

${ displaystyle u { partial u over partial x} + upsilon { partial u over partial y} = - {1 over rho} { partial p over partial x} + { nu } { partial ^ {2} u over partial y ^ {2}}}$

${ displaystyle {1 over rho} { partial p over partial y} = 0}$

и если жидкость несжимаема (как жидкости в стандартных условиях):

${ displaystyle { partial u over partial x} + { partial upsilon over partial y} = 0}$

Анализ порядка величины предполагает, что продольный масштаб длины значительно больше, чем поперечный масштаб длины внутри пограничного слоя. Отсюда следует, что изменения свойств в продольном направлении обычно намного ниже, чем в нормальном направлении стенки. Применение этого к уравнению неразрывности показывает, что ${ displaystyle upsilon}$, нормальная скорость стенки, мала по сравнению с ${ displaystyle u}$ продольная скорость.

Поскольку статическое давление ${ displaystyle p}$ не зависит от ${ displaystyle y}$, то давление на краю пограничного слоя - это давление во всем пограничном слое в данном продольном положении. Внешнее давление может быть получено путем применения Уравнение Бернулли. Позволять ${ displaystyle U}$ - скорость жидкости вне пограничного слоя, где ${ displaystyle u}$ и ${ displaystyle U}$ оба параллельны. Это дает при замене на ${ displaystyle p}$ следующий результат

${ displaystyle u { partial u over partial x} + upsilon { partial u over partial y} = U { frac {dU} {dx}} + { nu} { partial ^ {2 } u over partial y ^ {2}}}$

Для потока, в котором статическое давление ${ displaystyle p}$ также не меняет направление потока

${ displaystyle { frac {dp} {dx}} = 0}$

так ${ displaystyle U}$ остается постоянным.

Таким образом, уравнение движения упрощается и становится

${ displaystyle u { partial u over partial x} + upsilon { partial u over partial y} = { nu} { partial ^ {2} u over partial y ^ {2}} }$

Эти приближения используются в различных практических задачах, представляющих научный и технический интерес. Приведенный выше анализ предназначен для любого мгновенного ламинарный или же бурный пограничный слой, но используется в основном в исследованиях ламинарного потока, поскольку иметь в виду поток также является мгновенным потоком, потому что нет никаких колебаний скорости. Это упрощенное уравнение представляет собой параболическое уравнение в частных производных и может быть решено с использованием решения подобия, которое часто называют уравнением Пограничный слой Блазиуса.

Теорема транспозиции Прандтля

Прандтль^[2] заметил, что из любого решения ${ Displaystyle и (х, у, т), v (х, у, т)}$ которое удовлетворяет уравнениям пограничного слоя, дальнейшее решение ${ Displaystyle и ^ {*} (х, у, т), v ^ {*} (х, у, т)}$, который также удовлетворяет уравнениям пограничного слоя, можно построить, записав

${ displaystyle u ^ {*} (x, y, t) = u (x, y + f (x), t), quad v ^ {*} (x, y, t) = v (x, y + f (x), t) -f '(x) u (x, y + f (x), t)}$

куда ${ displaystyle f (x)}$ произвольно. Поскольку решение не является уникальным с математической точки зрения,^[3] к решению можно добавить любую из бесконечного набора собственных функций, как показано Стюартсон^[4] и Пол А. Либби.^[5][6]

Интеграл импульса фон Кармана

фон Карман^[7] вывел интегральное уравнение путем интегрирования уравнения пограничного слоя через пограничный слой в 1921 году. Уравнение имеет вид

${ displaystyle { frac { tau _ {w}} { rho U ^ {2}}} = { frac {1} {U ^ {2}}} { frac { partial} { partial t }} (U delta _ {1}) + { frac { partial delta _ {2}} { partial x}} + { frac {2 delta _ {2} + delta _ {1} } {U}} { frac { partial U} { partial x}} + { frac {v_ {w}} {U}}}$

куда

${ displaystyle tau _ {w} = mu left ({ frac { partial u} { partial y}} right) _ {y = 0}, quad v_ {w} = v (x, 0, t), quad delta _ {1} = int _ {0} ^ { infty} left (1 - { frac {u} {U}} right) , dy, quad delta _ {2} = int _ {0} ^ { infty} { frac {u} {U}} left (1 - { frac {u} {U}} right) , dy}$

${ Displaystyle тау _ {ш}}$ напряжение сдвига стенки, ${ displaystyle v_ {w}}$ - скорость всасывания / впрыска у стенки, ${ displaystyle delta _ {1}}$ - толщина вытеснения и ${ displaystyle delta _ {2}}$ - толщина импульса. Приближение Кармана – Польхаузена выводится из этого уравнения.

Интеграл энергии

Интеграл энергии был получен Wieghardt.^[8][9]

${ displaystyle { frac {2 varepsilon} { rho U ^ {3}}} = { frac {1} {U}} { frac { partial} { partial t}} ( delta _ { 1} + delta _ {2}) + { frac {2 delta _ {2}} {U ^ {2}}} { frac { partial U} { partial t}} + { frac { 1} {U ^ {3}}} { frac { partial} { partial x}} (U ^ {3} delta _ {3}) + { frac {v_ {w}} {U}} }$

куда

${ displaystyle varepsilon = int _ {0} ^ { infty} mu left ({ frac { partial u} { partial y}} right) ^ {2} dy, quad delta _ {3} = int _ {0} ^ { infty} { frac {u} {U}} left (1 - { frac {u ^ {2}} {U ^ {2}}} right ) , dy}$

${ displaystyle varepsilon}$ - скорость диссипации энергии из-за вязкости через пограничный слой и ${ displaystyle delta _ {3}}$ - энергетическая толщина.^[10]

Преобразование фон Мизеса

Для устойчивых двумерных пограничных слоев фон Мизес^[11] представил преобразование, которое требует ${ displaystyle x}$ и ${ displaystyle psi}$(функция потока ) как независимые переменные вместо ${ displaystyle x}$ и ${ displaystyle y}$ и использует зависимую переменную ${ displaystyle chi = U ^ {2} -u ^ {2}}$ вместо ${ displaystyle u}$. Тогда уравнение пограничного слоя станет

${ displaystyle { frac { partial chi} { partial x}} = nu { sqrt {U ^ {2} - chi}} , { frac { partial ^ {2} chi} { partial psi ^ {2}}}}$

Исходные переменные восстанавливаются из

${ displaystyle y = int { sqrt {U ^ {2} - chi}} , d psi, quad u = { sqrt {U ^ {2} - chi}}, quad v = u int { frac { partial} { partial x}} left ({ frac {1} {u}} right) , d psi.}$

Позднее это преобразование распространяется на сжимаемый пограничный слой с помощью фон Карман и HS Tsien.^[12]

Превращение Крокко

Для устойчивого двумерного сжимаемого пограничного слоя Луиджи Крокко^[13] представил преобразование, которое требует ${ displaystyle x}$ и ${ displaystyle u}$ как независимые переменные вместо ${ displaystyle x}$ и ${ displaystyle y}$ и использует зависимую переменную ${ Displaystyle тау = му частичное и / частичное у}$(напряжение сдвига) вместо ${ displaystyle u}$. Тогда уравнение пограничного слоя принимает вид

${ displaystyle { begin {align} & mu rho u { frac { partial} { partial x}} left ({ frac {1} { tau}} right) + { frac { partial ^ {2} tau} { partial u ^ {2}}} - mu { frac {dp} {dx}} { frac { partial} { partial u}} left ({ frac {1} { tau}} right) = 0, [5pt] & { text {if}} { frac {dp} {dx}} = 0, { text {then}} { frac { mu rho} { tau ^ {2}}} { frac { partial tau} { partial x}} = { frac {1} {u}} { frac { partial ^ { 2} tau} { partial u ^ {2}}}. End {выравнивается}}}$

Исходная координата восстанавливается из

${ displaystyle y = mu int { frac {du} { tau}}.}$

Турбулентные пограничные слои

Обработка турбулентных пограничных слоев намного сложнее из-за зависимого от времени изменения свойств потока. Одним из наиболее широко используемых методов борьбы с турбулентными потоками является применение Разложение Рейнольдса. Здесь мгновенные характеристики потока разлагаются на среднее значение и колеблющуюся составляющую. Применение этого метода к уравнениям пограничного слоя дает полные уравнения турбулентного пограничного слоя, которые не часто приводятся в литературе:

${ displaystyle { partial { overline {u}} over partial x} + { partial { overline {v}} over partial y} = 0}$

${ displaystyle { overline {u}} { partial { overline {u}} over partial x} + { overline {v}} { partial { overline {u}} over partial y} = - {1 over rho} { partial { overline {p}} over partial x} + nu left ({ partial ^ {2} { overline {u}} over partial x ^ {2}} + { partial ^ {2} { overline {u}} over partial y ^ {2}} right) - { frac { partial} { partial y}} ({ overline {u'v '}}) - { frac { partial} { partial x}} ({ overline {u' ^ {2}}})}$

${ displaystyle { overline {u}} { partial { overline {v}} over partial x} + { overline {v}} { partial { overline {v}} over partial y} = - {1 over rho} { partial { overline {p}} over partial y} + nu left ({ partial ^ {2} { overline {v}} over partial x ^ {2}} + { partial ^ {2} { overline {v}} over partial y ^ {2}} right) - { frac { partial} { partial x}} ({ overline {u'v '}}) - { frac { partial} { partial y}} ({ overline {v' ^ {2}}})}$

Используя аналогичный анализ по порядку величины, приведенные выше уравнения можно свести к членам высшего порядка. Выбирая шкалы длины ${ displaystyle delta}$ для изменений в поперечном направлении, и ${ displaystyle L}$ для изменений в продольном направлении, с ${ displaystyle delta << L}$, уравнение x-импульса упрощается до:

${ displaystyle { overline {u}} { partial { overline {u}} over partial x} + { overline {v}} { partial { overline {u}} over partial y} = - {1 over rho} { partial { overline {p}} over partial x} - { frac { partial} { partial y}} ({ overline {u'v '}} ).}$

Это уравнение не удовлетворяет условие противоскольжения у стены. Как Прандтль сделал для своих уравнений пограничного слоя, необходимо использовать новый, меньший масштаб длины, чтобы позволить вязкому члену стать ведущим порядком в уравнении импульса. Выбирая ${ displaystyle eta << delta}$ как у-масштаб, уравнение импульса ведущего порядка для этого "внутреннего пограничного слоя" задается следующим образом:

${ displaystyle 0 = - {1 over rho} { partial { overline {p}} over partial x} + { nu} { partial ^ {2} { overline {u}} over partial y ^ {2}} - { frac { partial} { partial y}} ({ overline {u'v '}}).}$

В пределе бесконечного числа Рейнольдса можно показать, что член градиента давления не влияет на внутреннюю область турбулентного пограничного слоя. Новая «внутренняя шкала длины» ${ displaystyle eta}$ представляет собой вязкую шкалу длины и имеет порядок ${ displaystyle { frac { nu} {и _ {*}}}}$, с ${ displaystyle u _ {*}}$ - масштаб скорости турбулентных пульсаций, в данном случае скорость трения.

В отличие от уравнений ламинарного пограничного слоя, наличие двух режимов, управляемых разными наборами масштабов потока (т.е.внутреннее и внешнее масштабирование) сделало поиск универсального решения подобия для турбулентного пограничного слоя трудным и противоречивым. Чтобы найти решение подобия, которое охватывает обе области потока, необходимо асимптотически согласовать решения из обеих областей потока. Такой анализ даст либо так называемый логарифм или же сила закона.

Дополнительный срок ${ displaystyle { overline {u'v '}}}$ в уравнениях турбулентного пограничного слоя известно как напряжение сдвига Рейнольдса и неизвестно априори. Поэтому решение уравнений турбулентного пограничного слоя требует использования модель турбулентности, цель которого - выразить напряжение сдвига Рейнольдса через известные переменные потока или производные. Отсутствие точности и универсальности таких моделей является основным препятствием на пути успешного прогнозирования свойств турбулентного потока в современной гидродинамике.

В пристеночной области существует слой постоянного напряжения. Из-за затухания флуктуаций вертикальной скорости у стенки член напряжения Рейнольдса станет незначительным, и мы обнаружим, что существует линейный профиль скорости. Это верно только для самых Пристенная область.

Тепломассообмен

В 1928 г. французский инженер Андре Левек наблюдал, что на конвективную теплопередачу в текущей жидкости влияют только значения скорости очень близко к поверхности.^[14][15] Для потоков с большим числом Прандтля изменение температуры / массы от температуры поверхности к температуре набегающего потока происходит в очень тонкой области, близкой к поверхности. Следовательно, наиболее важными являются скорости жидкости внутри этой очень тонкой области, в которой изменение скорости можно считать линейным с нормальным расстоянием от поверхности. Таким образом, для

${ displaystyle u (y) = U left [1 - { frac {(yh) ^ {2}} {h ^ {2}}} right] = U { frac {y} {h}} left [2 - { frac {y} {h}} right] ;,}$

когда ${ displaystyle y rightarrow 0}$, тогда

${ displaystyle u (y) приблизительно 2U { frac {y} {h}} = theta y,}$

куда θ является касательной параболы Пуазейля, пересекающей стену. Хотя решение Левека было специфическим для передачи тепла в поток Пуазейля, его идеи помогли другим ученым прийти к точному решению проблемы теплового пограничного слоя.^[16] Шу заметил, что в пограничном слое ты снова является линейной функцией у, но в этом случае касательная к стенке является функцией Икс.^[17] Он выразил это с помощью модифицированной версии профиля Левека:

${ Displaystyle и (у) = тета (х) у.}$

Это дает очень хорошее приближение даже для малых ${ displaystyle Pr}$ числа, так что только жидкие металлы с ${ displaystyle Pr}$ гораздо меньше единицы не может рассматриваться таким образом.^[16]В 1962 году Кестин и Персен опубликовали статью, описывающую решения для теплопередачи, когда тепловой пограничный слой полностью находится внутри импульсного слоя и для различных распределений температуры стенок.^[18] Для задачи о плоской пластине со скачком температуры при ${ displaystyle x = x_ {0}}$, они предлагают замену, которая сводит параболическое уравнение теплового пограничного слоя к обыкновенному дифференциальному уравнению. Решение этого уравнения, температура в любой точке жидкости, может быть выражено как неполное гамма-функция.^[15] Schlichting предложил эквивалентную замену, которая сводит уравнение теплового пограничного слоя к обыкновенному дифференциальному уравнению, решением которого является та же неполная гамма-функция.^[19]

Константы конвективного переноса из анализа пограничного слоя

Пол Рихард Генрих Блазиус получили точное решение вышеуказанного ламинарный пограничный слой уравнения.^[20] В толщина пограничного слоя ${ displaystyle delta}$ является функцией Число Рейнольдса для ламинарного потока.

${ displaystyle delta приблизительно 5,0 {x over { sqrt {Re}}}}$

${ displaystyle delta}$ = толщина пограничного слоя: область потока, где скорость меньше 99% скорости в дальней зоне ${ displaystyle v _ { infty}}$; ${ displaystyle x}$ находится вдоль полубесконечной пластины, а ${ displaystyle Re}$ это число Рейнольдса, определяемое ${ Displaystyle rho v _ { infty} х / му}$ (${ Displaystyle rho =}$ плотность и ${ Displaystyle mu =}$ динамическая вязкость).

В решении Блазиуса граничные условия используются в безразмерной форме:

${ displaystyle {v_ {x} -v_ {S} over v _ { infty} -v_ {S}} = {v_ {x} over v _ { infty}} = {v_ {y} over v_ { infty}} = 0}$     в     ${ displaystyle y = 0}$

${ displaystyle {v_ {x} -v_ {S} over v _ { infty} -v_ {S}} = {v_ {x} over v _ { infty}} = 1}$     в     ${ Displaystyle у = infty}$ и ${ displaystyle x = 0}$

Граничный слой скорости (верхний, оранжевый) и температурный пограничный слой (нижний, зеленый) имеют функциональную форму из-за сходства в балансах импульса / энергии и граничных условиях.

Обратите внимание, что во многих случаях граничное условие прилипания выполняется, что ${ displaystyle v_ {S}}$, скорость жидкости на поверхности пластины равна скорости пластины во всех точках. Если пластина не двигается, то ${ displaystyle v_ {S} = 0}$. Если допускается проскальзывание жидкости, требуется гораздо более сложный вывод.^[21]

Фактически, решение Блазиуса для ламинарного профиля скорости в пограничном слое над полубесконечной пластиной может быть легко расширено для описания пограничных слоев Thermal и Concentration для тепломассопереноса соответственно. Вместо дифференциального баланса x-импульса (уравнения движения) здесь используется аналогичный полученный баланс энергии и массы:

Энергия:         ${ displaystyle v_ {x} { partial T over partial x} + v_ {y} { partial T over partial y} = {k over rho C_ {p}} { partial ^ {2 } T over partial y ^ {2}}}$

Масса:           ${ displaystyle v_ {x} { partial c_ {A} over partial x} + v_ {y} { partial c_ {A} over partial y} = D_ {AB} { partial ^ {2} c_ {A} over partial y ^ {2}}}$

Для баланса количества движения кинематическая вязкость ${ displaystyle nu}$ можно считать коэффициент диффузии по импульсу. В энергетическом балансе это заменяется температуропроводностью ${ Displaystyle альфа = {к / ро C_ {P}}}$, а по массовой диффузии ${ displaystyle D_ {AB}}$ в балансе масс. По температуропроводности вещества ${ displaystyle k}$ его теплопроводность, ${ displaystyle rho}$ это его плотность и ${ displaystyle C_ {P}}$ его теплоемкость. Нижний индекс AB обозначает диффузность вида A, диффундирующего в вид B.

В предположении, что ${ Displaystyle альфа = D_ {AB} = nu}$, эти уравнения становятся эквивалентными балансу импульса. Таким образом, для числа Прандтля ${ Displaystyle Pr = nu / alpha = 1}$ и число Шмидта ${ Displaystyle Sc = nu / D_ {AB} = 1}$ решение Блазиуса применяется напрямую.

Соответственно, этот вывод использует родственную форму граничных условий, заменяя ${ displaystyle v}$ с ${ displaystyle T}$ или же ${ displaystyle c_ {A}}$ (абсолютная температура или концентрация вида A). Нижний индекс S обозначает состояние поверхности.

${ displaystyle {v_ {x} -v_ {S} over v _ { infty} -v_ {S}} = {T-T_ {S} over T _ { infty} -T_ {S}} = {c_ {A} -c_ {AS} over c_ {A infty} -c_ {AS}} = 0}$     в     ${ displaystyle y = 0}$

${ displaystyle {v_ {x} -v_ {S} over v _ { infty} -v_ {S}} = {T-T_ {S} over T _ { infty} -T_ {S}} = {c_ {A} -c_ {AS} over c_ {A infty} -c_ {AS}} = 1}$     в     ${ Displaystyle у = infty}$ и ${ displaystyle x = 0}$

С использованием функция оптимизации Блазиус получил следующее решение для напряжения сдвига на поверхности пластины.

${ displaystyle tau _ {0} = left ({ partial v_ {x} over partial y} right) _ {y = 0} = 0,332 {v _ { infty} over x} Re ^ { 1/2}}$

А через граничные условия известно, что

${ displaystyle {v_ {x} -v_ {S} over v _ { infty} -v_ {S}} = {T-T_ {S} over T _ { infty} -T_ {S}} = {c_ {A} -c_ {AS} over c_ {A infty} -c_ {AS}}}$

Нам даны следующие соотношения для потока тепла / массы от поверхности пластины

${ displaystyle left ({ partial T over partial y} right) _ {y = 0} = 0,332 {T _ { infty} -T_ {S} over x} Re ^ {1/2}}$

${ displaystyle left ({ partial c_ {A} over partial y} right) _ {y = 0} = 0,332 {c_ {A infty} -c_ {AS} over x} Re ^ {1 / 2}}$

Таким образом, для ${ Displaystyle Pr = Sc = 1}$

${ displaystyle delta = delta _ {T} = delta _ {c} = {5.0x over { sqrt {Re}}}}$

куда ${ displaystyle delta _ {T}, delta _ {c}}$ области течения, где ${ displaystyle T}$ и ${ displaystyle c_ {A}}$ меньше 99% их значений в дальней зоне.^[22]

Поскольку число Прандтля конкретной жидкости не всегда равно единице, немецкий инженер Э. Польхаузен, который работал с Людвиг Прандтль попытался эмпирически расширить эти уравнения, чтобы применить ${ displaystyle Pr neq 1}$. Его результаты могут быть применены к ${ displaystyle Sc}$ также.^[23] Он обнаружил, что для числа Прандтля больше 0,6 толщина теплового пограничного слоя было приблизительно дано:

График, показывающий относительную толщину пограничного слоя Thermal в зависимости от пограничного слоя Velocity (красный) для различных чисел Прандтля. За ${ displaystyle Pr = 1}$, эти двое равны.

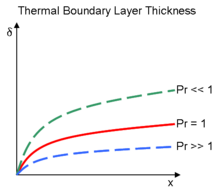
${ displaystyle { delta over delta _ {T}} = Pr ^ {1/3}}$          и поэтому          ${ displaystyle { delta over delta _ {c}} = Sc ^ {1/3}}$

Из этого решения можно охарактеризовать константы конвективного тепломассопереноса на основе области течения в пограничном слое. Закон проводимости Фурье и Закон охлаждения Ньютона суммируются с полученным выше термином потока и толщиной пограничного слоя.

${ displaystyle {q over A} = - k left ({ partial T over partial y} right) _ {y = 0} = h_ {x} (T_ {S} -T _ { infty} )}$

${ displaystyle h_ {x} = 0,332 {k over x} Re_ {x} ^ {1/2} Pr ^ {1/3}}$

Это дает локальную конвективную постоянную ${ displaystyle h_ {x}}$ в одной точке на полубесконечной плоскости. Интегрирование по длине пластины дает среднее значение

${ displaystyle h_ {L} = 0,664 {k over x} Re_ {L} ^ {1/2} Pr ^ {1/3}}$

После вывода с условиями массообмена (${ displaystyle k}$ = константа конвективного массопереноса, ${ displaystyle D_ {AB}}$ = диффузность вида A в разновидность B, ${ Displaystyle Sc = nu / D_ {AB}}$ ) получаются следующие решения:

${ displaystyle k '_ {x} = 0,332 {D_ {AB} over x} Re_ {x} ^ {1/2} Sc ^ {1/3}}$

${ displaystyle k '_ {L} = 0,664 {D_ {AB} over x} Re_ {L} ^ {1/2} Sc ^ {1/3}}$

Эти решения применимы для ламинарного потока с числом Прандтля / Шмидта более 0,6.^[22]

Военно-морская архитектура

Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Апрель 2009 г.)

Многие принципы, применимые к самолетам, также применимы к кораблям, подводным лодкам и морским платформам.

На кораблях, в отличие от самолетов, речь идет о несжимаемых потоках, где изменение плотности воды незначительно (повышение давления, близкое к 1000 кПа, приводит к изменению всего на 2–3 кг / м3.³). Эта область гидродинамики называется гидродинамикой. Корабельный инженер сначала занимается гидродинамикой, а уже потом - силой. Развитие, разрушение и разделение пограничного слоя становятся критическими, поскольку высокая вязкость воды создает высокие напряжения сдвига. Еще одним следствием высокой вязкости является эффект скользящего потока, при котором корабль движется, как копье, пронзающее губку с большой скоростью.^{[нужна цитата ]}

Турбина пограничного слоя

Этот эффект был использован в Турбина тесла, запатентовано Никола Тесла в 1913 году. Называется безлопастным турбина потому что он использует эффект пограничного слоя, а не жидкость, попадающую на лопасти, как в обычной турбине. Турбины пограничного слоя также известны как турбина когезионного типа, безлопастная турбина и турбина со слоем Прандтля (после Людвиг Прандтль ).

Прогнозирование толщины переходного пограничного слоя в цилиндре с помощью анализа размеров

Используя уравнения нестационарной и вязкой силы для цилиндрического потока, вы можете предсказать толщину переходного пограничного слоя, найдя число Уомерсли (${ displaystyle N_ {w}}$).

Переходная сила = ${ displaystyle rho vw}$

Вязкая сила = ${ displaystyle { mu v over delta _ {1} ^ {2}}}$

Уравнивание их друг другу дает:

${ displaystyle rho vw = { mu v over delta _ {1} ^ {2}}}$

Решение для дельты дает:

${ displaystyle delta _ {1} = { sqrt { mu over rho w}} = { sqrt { v over w}}}$

В безразмерном виде:

${ displaystyle {L over delta _ {1}} = {L { sqrt {w over v}}} = N_ {w}}$

куда ${ displaystyle N_ {w}}$ = Число Уомерсли; ${ displaystyle rho}$ = плотность; ${ displaystyle v}$ = скорость; ${ displaystyle w =}$ ?; ${ displaystyle delta _ {1}}$ = длина переходного пограничного слоя; ${ displaystyle mu}$ = вязкость; ${ displaystyle L}$ = характерная длина.

Прогнозирование условий конвективного течения в пограничном слое в цилиндре с использованием анализа размеров

Используя уравнения конвективной и вязкой силы в пограничном слое для цилиндрического потока, вы можете предсказать условия конвективного потока в пограничном слое, найдя безразмерное число Рейнольдса (${ displaystyle Re}$).

Конвективная сила: ${ displaystyle rho v ^ {2} over L}$

Вязкая сила: ${ displaystyle { mu v over delta _ {2} ^ {2}}}$

Уравнивание их друг другу дает:

${ displaystyle { rho v ^ {2} over L} = { mu v over delta _ {2} ^ {2}}}$

Решение для дельты дает:

${ displaystyle delta _ {2} = { sqrt { mu L over rho v}}}$

В безразмерном виде:

${ displaystyle {L over delta _ {2}} = { sqrt { rho vL over mu}} = { sqrt {Re}}}$

куда ${ displaystyle Re}$ = Число Рейнольдса; ${ displaystyle rho}$ = плотность; ${ displaystyle v}$ = скорость; ${ displaystyle delta _ {2}}$ = длина конвективного пограничного слоя; ${ displaystyle mu}$ = вязкость; ${ displaystyle L}$ = характерная длина.

Поглощение пограничного слоя

Поглощение пограничного слоя обещает увеличение топливная экономичность самолета с кормовым движитель глотая медленный фюзеляж пограничный слой и повторное включение будить уменьшить сопротивление и улучшить тяговая эффективность.Для работы в условиях искаженного воздушного потока вентилятор тяжелее, а его эффективность снижается, а его интеграция затруднена. Он используется в таких концепциях, как Аврора D8 или французское исследовательское агентство Онера Nova, экономия 5% в крейсерском режиме за счет поглощения 40% пограничного слоя фюзеляжа.^[24]

Airbus представил концепт Наутилиус на ICAS конгресс в сентябре 2018 г .: поглотить весь пограничный слой фюзеляжа при минимизации азимутальный искажение потока, фюзеляж разделяется на две оси с соотношением 13-18: 1 коэффициент байпаса Вентиляторы. КПД до 90% аналогичен вращающимся в противоположных направлениях. открытые роторы с меньшими, более легкими, менее сложными и шумными двигателями. Он может снизить расход топлива более чем на 10% по сравнению с обычным подкрыльевым двигателем с байпасным соотношением 15: 1.^[24]

Смотрите также

• Разделение пограничного слоя
• Толщина пограничного слоя
• Толщина и форма теплового пограничного слоя
• Отсос пограничного слоя
• Контроль пограничного слоя
• Пограничный слой Блазиуса
• Пограничный слой Фолкнера – Скан
• Слой Экмана
• Планетарный пограничный слой
• Логарифмический закон стены
• Коэффициент формы (поток в пограничном слое)
• Напряжение сдвига
• Поверхностный слой

Рекомендации

• Шансон, Х. (2009). Прикладная гидродинамика: введение в идеальные и реальные потоки жидкости. CRC Press, Taylor & Francis Group, Лейден, Нидерланды, 478 страниц. ISBN  978-0-415-49271-3.
• Полянин А. Зайцев, Справочник по нелинейным уравнениям с частными производными, Chapman & Hall / CRC Press, Бока-Ратон - Лондон, 2004. ISBN  1-58488-355-3
• Полянин А. Кутепов, А. Вязьмин, Д.А. Казенин, Гидродинамика, массо- и теплопередача в химической инженерии, Тейлор и Фрэнсис, Лондон, 2002. ISBN  0-415-27237-8
• Герман Шлихтинг, Клаус Герстен, Э. Краузе, Х. Младший Эртель, К. Мэйс "Теория пограничного слоя" 8-е издание Springer 2004 г. ISBN  3-540-66270-7
• Джон Д. Андерсон младший, "Пограничный слой Людвига Прандтля", Физика сегодня, Декабрь 2005 г.
• Андерсон, Джон (1992). Основы аэродинамики (2-е изд.). Торонто: S.S.CHAND. С. 711–714. ISBN  0-07-001679-8.
• Х. Теннекес и Дж. Л. Ламли, "Первый курс турбулентности", MIT Press, (1972).
• Лекции Уильяма К. Джорджа "Турбулентность для 21 века"

внешняя ссылка

• Национальная научная цифровая библиотека - пограничный слой
• Мур, Франклин К. "Эффект смещения трехмерного пограничного слоя "Отчет NACA 1124, 1953 г."
• Бенсон, Том "Пограничный слой ". НАСА Glenn Learning Technologies.
• Разделение пограничного слоя
• Уравнения пограничного слоя: точные решения - из EqWorld
• Джонс, Т. Пограничный теплообмен