Коробка Эджворта - Википедия - Edgeworth box

Рис. 1. Коробка Эджворта.

В экономика, Коробка Эджворта представляет собой графическое представление рынка всего с двумя товарами, Икс и Y, и два потребителя. Размеры ящика - это общие величины Ω_Икс и Ω_у из двух товаров.

Пусть потребителями будут Октавио и Эбби. Верхний правый угол поля представляет собой распределение, в котором Октавио держит все товары, а нижний левый соответствует полному владению Эбби. Точки в рамке представляют способы распределения товаров между двумя потребителями.

Рыночное поведение будет определяться потребителями. кривые безразличия. Синие кривые на диаграмме представляют кривые безразличия для Октавио и показаны выпуклыми с его точки зрения (то есть, если смотреть снизу слева). Оранжевые кривые относятся к Эбби и являются выпуклыми, если смотреть сверху справа. Перемещение вверх и вправо увеличивает распределение Октавио и помещает его на более желательную кривую безразличия, а Эбби - на менее желательную.

Обычным случаем считаются выпуклые кривые безразличия. Они соответствуют убывающей доходности каждого товара по отношению к другому.

Обмен на рынке начинается с первоначального распределения, известного как дар.

Поле Эджворта используется в основном для введения тем в теория общего равновесия в форме, в которой свойства могут быть визуализированы графически. Это также может показать сложность перехода к эффективному результату при наличии двусторонняя монополия.^[1] В последнем случае он служит предшественником проблема торга из теория игры что позволяет получить уникальное численное решение.^[2][3]

История

Разработка коробки Эджворта

Коробка Эджворта названа в честь Фрэнсис Исидро Эджворт,^[4] кто представил это в своей книге Математическая психика: эссе о применении математики в моральных науках, 1881.^[5]Первоначальное двухосное изображение Эджворта было преобразовано в уже знакомую прямоугольную диаграмму. Парето в его 1906 Руководство по политической экономии и был популяризирован в более поздней экспозиции Боули. Современную версию схемы обычно называют Коробка Эджворта-Боули.^[6]

Математическая теория экономического равновесия

Концептуальные основы равновесия в рыночной экономике были разработаны Леон Вальрас^[7] и далее расширен Вильфредо Парето.^[8] Он был исследован экономистами-математиками двадцатого века с пристальным вниманием к общности и строгости, включая Авраам Вальд,^[9] Пол Самуэльсон,^[10] Кеннет Эрроу и Жерар Дебре.^[11] Это было частью более широкого движения, в котором Уолд также стремился внести большую строгость в теория принятия решений и многие математики сосредоточились на минимизации зависимости от аксиома выбора.

Теория вальрасовских рынков постаралась найти самые общие предпосылки, из которых можно сделать данный вывод. Области, в которых можно усилить или ослабить помещения, включают:

• Являются ли функции дифференцируемыми;
• Являются ли кривые безразличия примитивными или производными от служебные функции; и
• Выпуклые ли кривые безразличия.

Предположения также носят более технический характер, например: необратимость, насыщенность, так далее.

Стремление к строгости не всегда способствует разборчивости речи. В этой статье кривые безразличия будут рассматриваться как примитивные. Сначала мы будем рассматривать их как выпуклые и дифференцируемые и сосредоточимся на внутренних равновесиях, но впоследствии мы ослабим эти предположения.

Рыночное равновесие

Рис. 2. Рынок коробок Эджворта.

Поскольку существует только два товара, эффективная цена - это обменный курс между ними. Наша цель состоит в том, чтобы найти цену, при которой может быть достигнуто рыночное равновесие, которая будет точкой, при которой дальнейшие операции не желательны, начиная с данного запаса. Эти количества будут определяться кривыми безразличия двух потребителей, как показано на рисунке 2.

Предположим, что каждый день Октавио и Эбби ходят на рынок с пожертвованиями. (ω_Икс, ω_у) и (Ω_Икс–Ω_Икс, Ω_у–Ω_у) двух товаров, соответствующих позиции ω на диаграмме. Два потребителя будут обмениваться между собой в условиях конкуренции на рынке. Это предположение требует некоторой приостановки недоверия, поскольку условия для идеальное соревнование - которые включают бесконечное количество потребителей - не удовлетворены.

Если два Икс'обмен на сингл Y, то транзакция Октавио и Эбби приведет их к некоторой точке вдоль сплошной серой линии, которая известна как бюджетная линия. (Чтобы быть более точным, бюджетную линию можно определить как прямую линию, проходящую через точку накопления, представляющую ассигнования, которые можно получить путем обмена по определенной цене.) Бюджетные линии для нескольких других цен также показаны пунктирными и пунктирными линиями на рис. 2.

Рис. 3. Равновесие в ящике Эджворта.

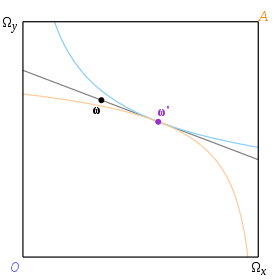
Равновесие, соответствующее данному наделению ω определяется парой кривых безразличия, которые имеют общую касательную, так что эта касательная проходит через ω. Мы будем использовать термин «ценовая линия» для обозначения общей касательной к двум кривым безразличия. Таким образом, равновесие соответствует бюджетной линии, которая также является ценовой линией, а цена в равновесии - это градиент этой линии. Рис. 3 ω это дар и ω' - это равновесное распределение.

Причина этого заключается в следующем.

Рис. 4. Деление квартала пересечением кривых безразличия.

Во-первых, любая точка в коробке должна лежать ровно на одной из кривых безразличия Эбби и ровно на одной из кривых Октавио. Если кривые пересекаются (как показано на рис. 4), они делят непосредственное соседство на четыре области, одна из которых (показана бледно-зеленой) предпочтительнее для обоих потребителей; поэтому точка, в которой пересекаются кривые безразличия, не может быть равновесием, а равновесие должно быть точкой касания.

Во-вторых, единственная цена, которая может удерживаться на рынке в точке касания, - это цена, заданная градиентом касательной, поскольку только по этой цене потребители будут готовы согласиться на ограниченно небольшие обмены.

И в-третьих (самый сложный момент) все биржи, ведущие потребителей по пути от ω чтобы равновесие происходило по той же цене. Если это принято, тогда эта цена должна быть единственной действующей в точке касания, и результат следует из этого.

В экономике с двумя людьми нет гарантии, что все обмены будут происходить по одинаковой цене. Но цель рамки Эджворта не в том, чтобы проиллюстрировать установление цен, которое может иметь место при отсутствии конкуренции, а в том, чтобы проиллюстрировать конкурентоспособную экономику в минимальном случае. Таким образом, мы можем представить себе, что вместо одной Эбби и одного Октавио у нас есть бесконечное количество клонов каждого, все они выходят на рынок с одинаковыми запасами в разное время и постепенно продвигаются к равновесию. Только что прибывший Октавио может обменяться по рыночной цене с Эбби, которая близка к равновесию, и пока только что прибывшая Эбби обменивается с почти довольным Октавио, цифры уравновешиваются. Чтобы обмен работал в условиях большой конкурентной экономики, для всех должна царить одна цена. Таким образом, биржа должна перемещать распределение по линии цены, как мы ее определили.^[12]

Соответственно, задача нахождения конкурентного равновесия сводится к задаче нахождения точки касания между двумя кривыми безразличия, касательная для которых проходит через данную точку. Использование предложения кривые (описанный ниже) предоставляет систематическую процедуру для этого.

Множество Парето

Рис. 5. Разделение бокса двумя касательными кривыми безразличия.

Распределение товаров называется «преобладанием по Парето» над другим, если это предпочтительно для одного потребителя и не хуже для другого. Распределение называется 'Оптимальный по Парето '(или «эффективное по Парето»), если никакое другое распределение не доминирует над ним. Набор оптимальных по Парето распределений известен как Множество Парето (или «эффективный локус»).

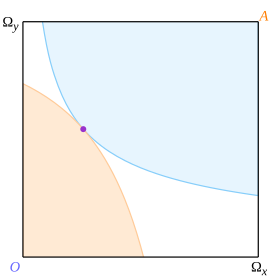
Рассмотрим пару касательных кривых, по одной для каждого потребителя, как показано на рис. 5, где точка касания показана фиолетовой точкой. Тогда выпуклость гарантирует, что кривые не могут пересекаться, кроме как в точке касания, и прямоугольник соответственно разделен на 3 области. Бледно-голубая область предпочтительнее для Октавио, но хуже для Эбби; бледно-оранжевая область предпочтительнее для Эбби, но хуже для Октавио; и белая область хуже для обоих. Аналогичные соображения применимы к границам. Отсюда следует, что точка касания оптимальна по Парето.

Рис. 6. Набор Парето (фиолетовая линия) для ящика Эджворта.

Таким образом, множество Парето - это геометрическое место точек касания кривых. Это линия, соединяющая происхождение Октавио (O) с местом происхождения Эбби (A). Пример показан на рис. 6, где фиолетовая линия - это множество Парето, соответствующее кривым безразличия для двух потребителей.

Словарь, используемый для описания различных объектов, входящих в блок Эджворта, расходится. Все множество Парето иногда называют кривая контракта, в то время как Mas-Colell et al. ограничьте определение контрактной кривой только теми точками на множестве Парето, которые обеспечивают как Эбби, так и Октавио, по крайней мере, такое же благополучие, как и при их первоначальном состоянии. Другие авторы, у которых есть больше теоретическая игра согнутые, такие как Мартин Осборн и Ариэль Рубинштейн,^[13] использовать термин основной для части набора Парето, которая по крайней мере так же хороша для каждого потребителя, как и первоначальный вклад.

Поскольку набор Парето - это набор точек, в которых кривые безразличия потребителей являются касательными, это также набор точек, в которых предельная норма замещения каждого потребителя равна таковой для другого человека.^[14]

Первая фундаментальная теорема экономики благосостояния

Мы видели, что точки касания кривых безразличия являются оптимумами Парето, но мы также видели ранее, что экономическое равновесие - это те точки, в которых кривые безразличия касаются общей линии цен. Отсюда следует, что равновесия - это в точности оптимумы Парето.

Этот аргумент применим с одним ограничением, даже если кривые недифференцируемы или если равновесие находится на границе. Условием равновесия является то, что никакого дальнейшего обмена не будет, а условием прекращения дальнейшего обмена является отсутствие направления движения, которое приносит пользу одному потребителю, не причиняя вреда другому; и это эквивалентно определению оптимума Парето.^[15]

Ограничение состоит в том, что из равновесия следует, что нет местный можно добиться улучшения - другими словами, точка будет оптимальной по Парето «локально». Но оптимальность по Парето в настоящее время считается глобальной по определению.^[16] Таким образом, если природа кривых безразличия допускает возникновение неглобальных оптимумов (чего не может произойти, если они выпуклые), тогда возможно, что равновесия не будут оптимальными по Парето.

Идеальное соревнование не является предварительным условием теоремы. До тех пор, пока потребители могут свободно обмениваться и будут продолжать делать это до тех пор, пока взаимоприемлемый обмен не станет доступным, равновесие будет достигнуто и будет (по крайней мере, «локально») оптимальным по Парето.^[17]

Вторая фундаментальная теорема экономики благосостояния

Рис. 7. Вторая теорема благосостояния.

Теперь рассмотрим экономику, в которой у потребителей есть пожертвования. ω как показано на рис. 7. Свободный рынок, предоставленный самим себе, приведет их к ω '. Но предположим, что какая-то другая позиция в коробке - скажем α ' - считается социально предпочтительным. Можно предположить, что социально желаемое положение является оптимальным по Парето.

Мы можем думать о ценовых линиях (показанных пунктирной линией на диаграмме) как о соответствующих различных распределениях реального дохода, а движение по ним - как о перераспределении ресурсов при неизменном доходе.

Затем, чтобы переместить общество в желаемую точку α ' правительству не обязательно перераспределять ресурсы таким образом, чтобы Октавио удерживал (α '_Икс, а '_у), а у Эбби есть дополнение: достаточно перераспределить ресурсы, чтобы экономика любой точка (скажем α) на ценовой линии через α ', а затем покинуть рынок, чтобы найти собственное равновесие. В самом деле, до тех пор, пока правительство признает желаемое распределение доходов, ему не нужно иметь никакого представления об оптимальном распределении ресурсов.

В утверждении для более общей экономики теорема будет восприниматься как утверждающая, что α ' может быть достигнута денежным переводом с последующей свободной рыночной игрой; но денег в ящике Эджворта нет.

Вторая фундаментальная теорема не дает плана избавления от болезней общества. Правительство может принять решение о перераспределении ресурсов между Октавио и Эбби, переместив их из ω к α перед дневной торговлей; и, как следствие, тот, кто проиграет, может решить на следующий день вывести на рынок меньше. Вторая фундаментальная теорема не учитывает искажения, вносимые перераспределением.^[18]

Кривые предложения

Рис. 8. Предпочтительные баллы по разным статьям бюджета.

Кривые предложения предоставляют средства нахождения точек равновесия, а также полезны для исследования их существования и уникальности.

В коробке можно нарисовать две такие кривые, по одной для каждого потребителя и обе в зависимости от обеспеченности. Мы меняем строку бюджета на ω и проследите точки, наиболее благоприятствующие двум потребителям, вдоль линии, как показано цветными точками на рис. 8. Это точки, в которых линия касается их собственных кривых безразличия.

Рис. 9. Кривые предложения

Место расположения точек наибольшего благоприятствования потребителя - это его кривая предложения. На рис. 9 кривая предложения Октавио показана темно-синей, а кривая Эбби - коричневой. Они встречаются в точке ω' и линия равновесного бюджета (нарисованная серым цветом) проходит через эту точку. Безразличие изгибается ω' для двух потребителей показаны более светлыми цветами.

Кривая предложения обязательно проходит через точку эндаумента ω. Если мы возьмем Эбби в качестве примера, мы заметим, что одна из ее кривых безразличия должна проходить через ω и что линия бюджета может быть выбрана так, чтобы иметь тот же градиент, что и кривая безразличия здесь, делая ω наиболее удачная точка для этой линии.

Вследствие этого кривые предложения двух потребителей обязательно пересекаются в ω; но свойство, которое делает это возможным, заключается в том, что ω это единственная возможная точка пересечения, соответствующая бюджетным линиям с различным градиентом, и поэтому она не обязательно составляет равновесие.

Любое пересечение кривых предложения в точке, отличной от ω определяет устойчивое равновесие. Если две кривые предложения касаются точки накопления, тогда эта точка действительно является равновесием, а их общая касательная - это соответствующая бюджетная линия.^[19]

Терминология для кривых предложения

Кривые предложения были впервые использованы Вильфредо Парето - увидеть его Мануале/Мануэль Глава. III, §97. Он назвал их «кривыми обмена» (Linee Dei Baratti/lignes des échanges), и его имя для предпочтительного распределения Октавио по строке бюджета было его «точкой равновесия».

Это предпочтительное распределение в наши дни иногда называют «требованием» Октавио, которое представляет собой асимметричное описание симметричного факта. Распределение определяет владение Эбби в такой же степени, как и у Октавио, и, следовательно, в такой же степени является предложением, как и спросом.

Offre по-французски означает «предложение», поэтому называть кривую предложения локусом спроса равносильно называть кривой предложения локусом спроса.

Уникальность равновесий

Рис. 10. Ящик Эджворта с множественными равновесиями.

Рис. 11. Ящик Эджворта с множественными положениями равновесия (деталь)

Из экономических соображений можно было бы предположить, что если существует общая касательная через данное наделение и если кривые безразличия не являются патологическими по своей форме, то точка касания будет уникальной. Это оказалось неправдой. Условия единственности равновесия были предметом обширных исследований: см. Теория общего равновесия.

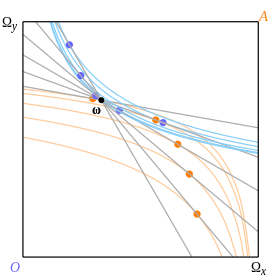
Рис. 9 и 10 иллюстрируют пример от Mas-Colell et al. в котором три различных состояния равновесия соответствуют точке наделения ω. Кривые безразличия:

${ displaystyle quad x - { tfrac {1} {8}} y ^ {- 8} = u}$ (Октавио)

${ displaystyle quad y - { tfrac {1} {8}} x ^ {- 8} = u}$ (Эбби).

Кривые безразличия заполняют поле, но отображаются только по касательной к некоторым репрезентативным статьям бюджета. Кривые предложения, нарисованные на рис. 11, пересекаются в трех точках, показанных большими серыми точками и соответствующих обменным курсам¹⁄₂, 1 и 2.

Обобщения

Ранние исследования свойств равновесия основывались на неявном определении касания, а выпуклость, по-видимому, предполагалась неявно.^[20] Не было сомнений, что равновесие будет достигнуто: градиентный подъем приведет к этому. Но результатам не хватало общности.

Граничные положения равновесия и недифференцируемые кривые

Рис. 12. Линии цен для бокса с граничными положениями равновесия.

Кеннет Эрроу и Жерар Дебре независимо друг от друга опубликовали статьи в 1951 году, обратив внимание на ограничения в исчислении доказательств теорем о равновесии.^[21] Эрроу особо упомянул трудность, вызванную равновесием на границе, а Дебрё - проблему недифференцируемых кривых безразличия.

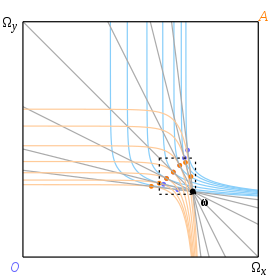
Не стремясь к исчерпывающему охвату, легко увидеть в интуитивно понятных терминах, как расширить наши методы для применения в этих случаях. Нам необходимо расширить понятие касательной, включив в нее любую линию, которая касается кривой: касательную в этимологическом смысле, а не в дифференциальном исчислении. В примере на рис. 12 есть дуга законных ценовых линий через точку соприкосновения, каждая из которых касается кривых безразличия, не разрезая их внутри рамки, и, соответственно, существует диапазон возможных равновесий для данного фонда.

Конкурентное равновесие

Равновесия на рис. 12 не являются точками, в которых кривые касаются друг друга. Однако у них есть свойство, которое обобщает определение в терминах касательных, а именно, что две кривые могут быть локально разделены прямой линией.

Эрроу и Дебре определили равновесие так же, как и друг друга, в своих (независимых) статьях 1951 года, не предоставив никаких источников или обоснований для их определения. Они сохранили свое определение в своей совместной статье (о существовании равновесия) 1954 года.^[22] Новое определение потребовало изменения математической техники с дифференциального исчисления на выпуклый набор теория.

Фактически их определение было таким: равновесие, достижимое за счет пожертвований. ω состоит из распределения Икс и бюджетную строку через Икс и ω так что на линии нет точки, которую потребитель (строго) предпочитает Икс. Пара, состоящая из размещения и линии, удовлетворяющей этому свойству, известна как «вальрасианская» или 'конкурентное равновесие.

Рис. 13. «Локальное» равновесие.

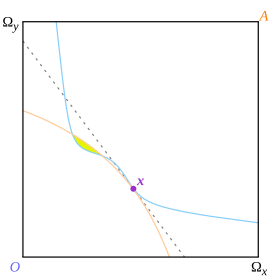
Бюджетная линия этого определения - это линия, которая разделяет кривые безразличия двух потребителей, но делает это. глобально а не локально. Эрроу и Дебре не объясняют, почему они требуют глобального разделения, которое, возможно, облегчило их доказательства, но, как можно видеть, имеет неожиданные последствия. На рис.13 точка Икс - точка касания, которая также является точкой, в которой кривые безразличия локально разделены пунктирной линией цен; но поскольку они не разделены глобально, точка не является равновесием согласно определению Эрроу и Дебре.

Рис. 14. Оптимум Парето, не являющийся «конкурентным равновесием».

На рис.14 точка Икс является оптимумом Парето, который не удовлетворяет определению конкурентного равновесия. Вопрос о том, будет ли экономика селиться в такой момент совершенно не зависит от того, удовлетворяет ли он данному определению равновесия; видимо, в этом случае он действительно поселился бы там.

Эрроу и Дебре всегда включали выпуклость кривых безразличия в свои «предположения». Термин «допущения» является расплывчатым, он может относиться как к предпосылкам, лежащим в основе определений, так и к теоремам, или к посылке, необходимой только для последних. Учитывая, что их определение не включает все положения равновесия, которые могут существовать, когда кривые могут быть невыпуклыми, возможно, что они имели в виду предположение о выпуклости в первом смысле. Независимо от того, так это или нет, определение было широко принято без каких-либо ограничений домена.

Иногда было обнаружено, что результаты могут быть получены в соответствии с их определением, не предполагая выпуклости в доказательстве (примером является первая фундаментальная теорема экономики благосостояния).

Наличие конкурентного равновесия

В некоторых странах не будет точки покоя, достижимой для данного вклада путем обмена по единым ценам; следовательно, не существует точки покоя, удовлетворяющей определению конкурентного равновесия. Семейства кривых рисунка на рис. 14 являются примером этого.

Основные теоремы экономики благосостояния

Когда равновесие определяется как «конкурентное равновесие», первая фундаментальная теорема может быть доказана, даже если кривые безразличия не обязательно должны быть выпуклыми: любое конкурентное равновесие является (глобально) оптимальным по Парето. Однако доказательство уже не очевидно, и читатель отсылается к статье о Основные теоремы экономики благосостояния.

Тот же самый результат не считался бы справедливым (с невыпуклыми кривыми безразличия) при определении равновесия касанием. Смысл Икс на рис. 13 можно было бы считать равновесием, которое нет (в глобальном масштабе) оптимально, так как в нем преобладает желтый регион по Парето.

Из этого не следует, что результат был усилен, поскольку достижимость равновесия была поставлена ​​под сомнение. На рис.13 точка Икс может и не быть «конкурентным равновесием», но экономика может застрять в нем, не позволяя ей достичь «истинного» (и оптимального по Парето) равновесия в желтой области.

Для первой теоремы о благосостоянии всегда считалось важным достижение равновесия. Лернер интерпретировал эту теорему следующим образом: «К счастью, оптимальное распределение товаров может быть достигнуто автоматически».^[23] Однако ничто не может гарантировать, что глобальный оптимум будет достигнут при наличии локальных оптимумов. Если концепция равновесия включает локальные оптимумы, такие как Икс, тогда равновесие может быть достигнуто, но неоптимально; если такие точки исключить, то равновесие может быть оптимальным, но недостижимым.

Различия, вызванные невыпуклостью, становятся более глубокими, если мы посмотрим на вторую фундаментальную теорему. Не каждый оптимум Парето является конкурентным равновесием (хотя он все еще может быть местом отдыха для экономики). Следовательно, в теореме необходимо либо дать выпуклость предпочтений как предпосылку, либо сформулировать так, чтобы «равновесие» не понималось как «конкурентное равновесие», как определено выше.

Примечания

Рекомендации

• Мас-Колелл, Андреу; Whinston, Michael D .; Джерри Р. Грин (1995). Микроэкономическая теория. Нью-Йорк: Издательство Оксфордского университета. ISBN  0-19-507340-1.
• Вильфредо Парето, Manuale di Economia Politica con una Introduzione alla Scienza Sociale (1906) / Мануэль д'Экономи Политик (1909) (фактически второе издание итальянской версии), англ. тр. (французов) как «Руководство по политической экономии» (1971). Текст на итальянском языке доступен на сайте https://archive.org/details/manualedieconomi00pareuoft.

внешняя ссылка

• Моделирование на Wolfram.com
• Объяснение коробки Эджворта на сайте Economic-True
• Объяснение коробки Эджворта в Digital Economist