Гомеоморфизм (теория графов) - Википедия - Homeomorphism (graph theory)

В теория графов, два графика ${ displaystyle G}$ и ${ displaystyle G '}$ находятся гомеоморфный если есть изоморфизм графов от некоторых подразделение из ${ displaystyle G}$ некоторым подразделение из ${ displaystyle G '}$ . Если ребра графа рассматриваются как линии, соединяющие одну вершину с другой (как они обычно изображаются на иллюстрациях), то два графа гомеоморфны друг другу в теоретико-графическом смысле именно в том случае, если они гомеоморфный в том смысле, в котором этот термин используется в топология.^[1]

Подразделение и сглаживание

В целом подразделение графа грамм (иногда известный как расширение^[2]) - граф, полученный в результате разбиения ребер в грамм. Подразделение некоторого края е with endpoints {ты,v} дает граф, содержащий одну новую вершину ш, и с набором кромок, заменяющим е двумя новыми ребрами, {ты,ш} и {ш,v}.

Например, край е, с конечными точками {ты,v}:

можно разделить на два ребра, е₁ и е₂, соединяясь с новой вершиной ш:

Обратная операция, сглаживание или же сглаживание вершина ш что касаемо пары ребер (е₁, е₂) инцидент на ш, удаляет оба ребра, содержащие ш и заменяет (е₁, е₂) с новым ребром, которое соединяет другие конечные точки пары. Здесь подчеркивается, что сглаживать можно только 2-валентные вершины.

Например, простой связаны граф с двумя ребрами, е₁ {ты,ш} и е₂ {ш,v}:

имеет вершину (а именно ш), которые можно сгладить, что приведет к:

Определение того, нужны ли графики грамм и ЧАС, ЧАС гомеоморфен подграфу из грамм, является НП-полный проблема.^[3]

Барицентрические подразделения

В барицентрическое подразделение подразделяет каждое ребро графа. Это особое подразделение, так как оно всегда приводит к двудольный граф. Эту процедуру можно повторить, чтобы п^th барицентрическое подразделение - это барицентрическое подразделение п−1^th барицентрическое подразделение графа. Второе такое подразделение всегда простой график.

Встраивание на поверхность

Очевидно, что разбиение графа сохраняет планарность. Теорема Куратовского утверждает, что

а конечный граф является планарный если и только если он не содержит подграф гомеоморфный к K₅ (полный график на пять вершины ) или же K_3,3 (полный двудольный граф на шести вершинах, три из которых соединяются с каждой из трех других).

Фактически, граф, гомеоморфный K₅ или же K_3,3 называется Подграф Куратовского.

Обобщение, вытекающее из Теорема Робертсона – Сеймура, утверждает, что для каждого целого числа грамм, существует конечная набор препятствий графиков ${ Displaystyle L (г) = влево {G_ {я} ^ {(г)} вправо }}$ такой, что граф ЧАС встраивается на поверхность род грамм если и только если ЧАС не содержит гомеоморфных копий любого из ${ Displaystyle G_ {я} ^ {(г)}}$ . Например, ${ Displaystyle L (0) = влево {K_ {5}, K_ {3,3} right }}$ состоит из подграфов Куратовского.

Пример

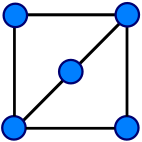
В следующем примере график грамм и график ЧАС гомеоморфны.

График грамм

График ЧАС

Если ГРАММ' - граф, созданный путем разбиения внешних ребер грамм и ЧАС' - это граф, созданный путем разбиения внутреннего края ЧАС, тогда ГРАММ' и ЧАС' есть аналогичный рисунок графика:

График ГРАММ', ЧАС'

Следовательно, существует изоморфизм между ГРАММ' и ЧАС', смысл грамм и ЧАС гомеоморфны.

Смотрите также

Рекомендации

^ Архидьякон, Дэн (1996), "Топологическая теория графов: обзор", Обзоры по теории графов (Сан-Франциско, Калифорния, 1995), Congressus Numerantium, 115, стр. 5–54, МИСТЕР 1411236, Название возникает потому, что ${ displaystyle G}$ и ${ displaystyle H}$ гомеоморфны как графы тогда и только тогда, когда они гомеоморфны как топологические пространства
^ Трюдо, Ричард Дж. (1993). Введение в теорию графов (Исправленное, расширенное переиздание. Ред.). Нью-Йорк: Dover Pub. п. 76. ISBN 978-0-486-67870-2. Получено 8 августа 2012. Определение 20. Если к некоторым ребрам графа добавить несколько новых вершин степени 2 грамм, получившийся граф ЧАС называется расширение из грамм.
^ Наиболее часто изучаемая проблема в литературе под названием проблема гомеоморфизма подграфов заключается в том, является ли подразделение ЧАС изоморфен подграфу грамм. Случай, когда ЧАС является п-вершинный цикл эквивалентен Гамильтонов цикл проблема и, следовательно, NP-полная. Однако эта формулировка эквивалентна только вопросу о том, ЧАС гомеоморфен подграфу из грамм когда ЧАС не имеет вершин степени два, так как не допускает сглаживания в ЧАС. NP-полную поставленную задачу можно показать с помощью небольшой модификации редукции гамильтонова цикла: добавить по одной вершине в каждую из ЧАС и грамм, смежная со всеми остальными вершинами. Таким образом, одновершинное увеличение графа грамм содержит подграф, гомеоморфный (п + 1) -вертекс колесо графа, если и только если грамм гамильтоново. Относительно трудностей проблемы гомеоморфизма подграфов см., Например, LaPaugh, Andrea S .; Ривест, Рональд Л. (1980), "Проблема гомеоморфизма подграфа", Журнал компьютерных и системных наук, 20 (2): 133–149, Дои:10.1016/0022-0000(80)90057-4, МИСТЕР 0574589.

Йеллен, Джей; Гросс, Джонатан Л. (2005), Теория графов и ее приложения, Дискретная математика и ее приложения (2-е изд.), Бока-Ратон: Chapman & Hall / CRC, ISBN 978-1-58488-505-4

[1] Архидьякон, Дэн (1996), "Топологическая теория графов: обзор", Обзоры по теории графов (Сан-Франциско, Калифорния, 1995), Congressus Numerantium, 115, стр. 5–54, МИСТЕР 1411236, Название возникает потому, что ${ displaystyle G}$ и ${ displaystyle H}$ гомеоморфны как графы тогда и только тогда, когда они гомеоморфны как топологические пространства

[2] Трюдо, Ричард Дж. (1993). Введение в теорию графов (Исправленное, расширенное переиздание. Ред.). Нью-Йорк: Dover Pub. п. 76. ISBN 978-0-486-67870-2. Получено 8 августа 2012. Определение 20. Если к некоторым ребрам графа добавить несколько новых вершин степени 2 грамм, получившийся граф ЧАС называется расширение из грамм.

[3] Наиболее часто изучаемая проблема в литературе под названием проблема гомеоморфизма подграфов заключается в том, является ли подразделение ЧАС изоморфен подграфу грамм. Случай, когда ЧАС является п-вершинный цикл эквивалентен Гамильтонов цикл проблема и, следовательно, NP-полная. Однако эта формулировка эквивалентна только вопросу о том, ЧАС гомеоморфен подграфу из грамм когда ЧАС не имеет вершин степени два, так как не допускает сглаживания в ЧАС. NP-полную поставленную задачу можно показать с помощью небольшой модификации редукции гамильтонова цикла: добавить по одной вершине в каждую из ЧАС и грамм, смежная со всеми остальными вершинами. Таким образом, одновершинное увеличение графа грамм содержит подграф, гомеоморфный (п + 1) -вертекс колесо графа, если и только если грамм гамильтоново. Относительно трудностей проблемы гомеоморфизма подграфов см., Например, LaPaugh, Andrea S .; Ривест, Рональд Л. (1980), "Проблема гомеоморфизма подграфа", Журнал компьютерных и системных наук, 20 (2): 133–149, Дои:10.1016/0022-0000(80)90057-4, МИСТЕР 0574589.

[1]

[2]

[3]