График Лавеса - Википедия - Laves graph

График Лавеса

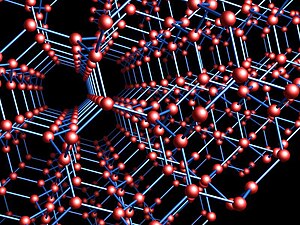
В геометрия и кристаллография, то График Лавеса бесконечный кубический симметричный граф. Его можно встроить в трехмерное пространство, с целочисленными координатами, чтобы сформировать структуру с киральная симметрия^[1] в котором три ребра в каждой вершине образуют углы 120 ° друг к другу. Его также можно определить более абстрактно как покрывающий граф из полный график на четырех вершинах.^[1]^[2]

Х. С. М. Коксетер (1955 ) назвал этот граф в честь Фриц Лавес, который первым написал об этом как Кристальная структура в 1932 г.^[3]^[4] Его также называли K₄ кристалл,^[5] (10,3) -сеть,^[6]^[7] алмазный близнец,^[8] триамонд,^[9]^[10] и srs net.^[11]

Конструкции

Из целочисленной сетки

В правильный косой многогранник на которую можно вписать граф Лавеса

В качестве Кокстер (1955) описывает, вершины графа Лавеса могут быть определены путем выбора одной из каждых восьми точек в трехмерном целочисленная решетка, и формируя их граф ближайшего соседа. В частности, выбираются точки

{ Displaystyle (0,0,0), quad (1,2,3), quad (2,3,1), quad (3,1,2),}

{ displaystyle (2,2,2), quad (3,0,1), quad (0,1,3), quad (1,3,0),}

и все другие точки, которые могут быть образованы добавлением к этим координатам числа, кратного четырем. Ребра графа Лавеса соединяют пары точек, Евклидово расстояние друг от друга квадратный корень из двух, ${ displaystyle { sqrt {2}}}$ (эти пары отличаются на одну единицу в двух координатах и одинаковы в третьей координате). Остальные несмежные пары вершин находятся дальше друг от друга, на расстоянии не менее ${ displaystyle { sqrt {6}}}$ друг от друга. Края получившегося геометрический график находятся диагонали подмножества граней правильный косой многогранник с шестью квадратными гранями на вершину, поэтому граф Лавеса встроенный в этом косом многограннике.^[3]

Можно чередовать две копии структуры, заполняя одну четверть точек целочисленной решетки, сохраняя при этом тот факт, что соседние вершины - это в точности пары точек, которые ${ displaystyle { sqrt {2}}}$ единиц, а все остальные пары точек - дальше друг от друга. Две копии являются зеркальным отображением друг друга.^[6]^[11]

Как покрывающий граф

Как абстрактный граф, граф Лавеса может быть построен как максимальный абелевский покрывающий граф из полный график ${ displaystyle K_ {4}}$ . Будучи покрывающим графом ${ displaystyle K_ {4}}$ означает, что есть математическая подгруппа из симметрии графа Лавеса такая, что когда вершины, симметричные друг другу в этой подгруппе, собираются вместе в орбиты подгруппы имеется четыре орбиты, и каждая пара орбит соединена ребрами графа друг с другом. То есть граф, вершины которого являются орбитами, а ребра - смежными парами орбит, точно равен ${ displaystyle K_ {4}}$ . Абелев накрывающий граф означает, что эта подгруппа симметрий является абелева группа (в этом случае группа ${ Displaystyle mathbb {Z} ^ {3}}$ образованный сложением трехмерного целого числа векторов ), и быть максимальным абелевым графом покрытия означает, что нет другого графа покрытия ${ displaystyle K_ {4}}$ с многомерной абелевой группой. Эта конструкция оправдывает одно из альтернативных названий графа Лавеса - ${ displaystyle K_ {4}}$ кристалл.^[1]

Один из способов построить максимальный абелев накрывающий граф из меньшего графа ${ displaystyle G}$ (в этом случае ${ displaystyle K_ {4}}$ ) заключается в выборе остовное дерево из ${ displaystyle G}$ , позволять ${ displaystyle d}$ быть количеством ребер, не входящих в остовное дерево (в данном случае, трех ребер, не являющихся деревьями), и для выбора отдельного единичный вектор в ${ Displaystyle mathbb {Z} ^ {d}}$ для каждого из этих недревесных ребер. Затем зафиксируем множество вершин графа покрытия как упорядоченные пары ${ displaystyle (v, w)}$ куда ${ displaystyle v}$ является вершиной ${ displaystyle G}$ и ${ displaystyle w}$ вектор в ${ Displaystyle mathbb {Z} ^ {d}}$ . Для каждой такой пары и каждого ребра ${ displaystyle uv}$ рядом с ${ displaystyle v}$ в ${ displaystyle G}$ , получить преимущество от ${ displaystyle (v, w)}$ к ${ Displaystyle (и, ш п эпсилон)}$ куда ${ displaystyle epsilon}$ равно нулю, если ${ displaystyle uv}$ принадлежит остовному дереву и в противном случае является базисным вектором, связанным с ${ displaystyle uv}$ , а где знак плюс или минус выбирается в соответствии с направлением, в котором проходит кромка. Полученный граф не зависит от выбора остовного дерева, и ту же конструкцию можно интерпретировать более абстрактно, используя теорию гомология.^[2]

Используя ту же конструкцию, шестиугольная черепица плоскости является графом максимального абелевого накрытия трехреберного дипольный график, а алмаз кубический - максимальный абелев накрывающий граф четырехреберного диполя. В ${ displaystyle d}$ -мерная целочисленная решетка (с ребрами единичной длины) - это максимальный абелев накрывающий граф графа с одной вершиной и ${ displaystyle d}$ петли.^[1]

Характеристики

График Лавеса - это кубический граф (в каждой вершине ровно по три ребра) и симметричный граф (каждая инцидентная пара вершины и ребра может быть преобразована в любую другую такую пару с помощью симметрии графа). В обхват этой структуры 10 - кратчайшие циклы в графе имеют 10 вершин - и 15 из этих циклов проходят через каждую вершину.^[1]^[3]^[11]

Ячейки Диаграмма Вороного этой структуры гептадекаэдры по 17 лиц. Они есть плезиоэдры, многогранники, что пространство плитки изоэдрально. Эксперименты со структурами, образованными этими многогранниками, привели Алана Шона к открытию гироид минимальная поверхность.^[12]

Один из четырех кубических индуцированные подграфы из график единичного расстояния на трехмерной целочисленной решетке с обхватом 10 изоморфный графу Лавеса.^[13]

Физические примеры

Молекулярные кристаллы

Расчеты показывают, что граф Лавеса может служить образцом для метастабильный или, возможно, нестабильный аллотроп углерода.^[5]^[8] Нравиться графит, каждый атом в структуре связан с тремя другими атомами, но в графите смежные атомы имеют те же плоскости связи, что и друг друга, тогда как в этой структуре плоскости связи соседних атомов скручены относительно друг друга вокруг линии, образованной связью, с углом закручивания примерно 70,5 °.

График Лавеса также может дать кристаллическая структура для бора; расчеты предсказывают, что это должно быть стабильно.^[14] Другие химические вещества, которые могут образовывать эту структуру, включают SrSi.₂, и элементаль азот.^[11]^[14]

Другой

Структура графа Лавеса и гироид поверхности, полученные из него, также наблюдались экспериментально в системах мыльная вода и в хитин сети бабочка крыловые чешуи.^[11]

внешняя ссылка

Баэз, Джон (14 октября 2016 г.), "График Лавеса", Визуальное понимание, Американское математическое общество

[sunada-1] а ^б ^c ^d ^е Сунада, Тошиказу (2008), «Кристаллы, которые природа может упустить» (PDF), Уведомления Американского математического общества, 55 (2): 208–215, МИСТЕР 2375022. Сунада, Тошиказу (2008), «Исправление: кристаллы, которые природа может пропустить» (PDF), Уведомления Американского математического общества, 55 (3): 343.

[biggs-2] а ^б Биггс, Н. (1984), "Гомологические накрытия графов", Журнал Лондонского математического общества, Вторая серия, 30 (1): 1–14, Дои:10.1112 / jlms / s2-30.1.1, МИСТЕР 0760867.

[coxeter-3] а ^б ^c Кокстер, Х. С. М. (1955), «О графике Лавеса обхвата десять», Канадский математический журнал, 7: 18–23, Дои:10.4153 / CJM-1955-003-7, МИСТЕР 0067508.

[4] Лавес, Ф. (1932), "Zur Klassifikation der Silikate. Geometrische Untersuchungen möglicher Silicium-Sauerstoff-Verbände als Verknüpfungsmöglichkeiten Regärer Tetraeder", Zeitschrift für Kristallographie, 82 (1): 1–14, Дои:10.1524 / zkri.1932.82.1.1.

[prl09-5] а ^б Ито, Масахиро; Котани, Мотоко; Найто, Хисаши; Сунада, Тошиказу; Кавазоэ, Ёсиюки; Адсчири, Тадафуми (2009), «Новый металлический кристалл углерода», Письма с физическими проверками, 102 (5): 055703, Bibcode:2009PhRvL.102e5703I, Дои:10.1103 / PhysRevLett.102.055703, PMID 19257523.

[hart-6] а ^б Харт, Джордж У., Сеть (10, 3) -a, получено 2014-11-30.

[7] Уэллс, А. Ф. (1940), "X. Конечные комплексы в кристаллах: классификация и обзор", Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал, Серия 7, 30 (199): 103–134, Дои:10.1080/14786444008520702.

[tlnkk-8] а ^б Тагами, Макото; Лян, Юнье; Найто, Хисаши; Кавазоэ, Ёсиюки; Котани, Мотоко (2014), "Отрицательно изогнутые кубические кристаллы углерода с октаэдрической симметрией", Углерод, 76: 266–274, Дои:10.1016 / j.carbon.2014.04.077.

[9] Ланье, Джарон (2009), «От плоских моделей к многогранникам», Американский ученый.

[10] Секин, Карло Х. (2008), «Сложные изоэдральные мозаики трехмерного евклидова пространства» в Сарханги, Реза; Секин, Карло Х. (ред.), Мосты Леуварден: математика, музыка, искусство, архитектура, культура, Лондон: Tarquin Publications, стр. 139–148, ISBN 9780966520194.

[srs-11] а ^б ^c ^d ^е Хайд, Стивен Т.; О'Киф, Майкл; Просерпио, Давид М. (2008), «Краткая история неуловимой, но вездесущей структуры в химии, материалах и математике» (PDF), Angewandte Chemie International Edition, 47 (42): 7996–8000, Дои:10.1002 / anie.200801519, PMID 18767088.

[12] Шен, Алан Х. (июнь – июль 2008 г.), «На графике (10,3) -а» (PDF), Уведомления Американского математического общества, 55 (6): 663.

[haugland-13] Хаугланд, Ян Кристиан (2003), "Классификация некоторых подграфов трехмерной сетки", Журнал теории графов, 42: 34–60, Дои:10.1002 / jgt.10071.

[boron-14] а ^б Дай, Джун; Ли, Чжэньюй; Ян, Цзиньлун (2010), «Борон» K₄ кристалл: стабильный хиральный трехмерный sp² сеть", Физическая химия Химическая физика, 12 (39): 12420–12422, Bibcode:2010PCCP ... 1212420D, Дои:10.1039 / C0CP00735H, PMID 20820588.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]