Лунный узел - Lunar node
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Январь 2018) (Узнайте, как и когда удалить этот шаблон сообщения) |
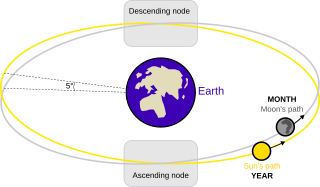
А лунный узел один из двух орбитальные узлы из Луна, то есть две точки, в которых орбита Луны пересекает в эклиптика. В Восходящий (или же север) узел, где Луна движется в северную эклиптическое полушарие, в то время как нисходящий (или же юг) узел находится там, где Луна входит в южное полушарие эклиптики.
А лунное затмение может произойти только тогда, когда полнолуние находится близко (в пределах 11 ° 38 'эклиптической долготы) к любому лунному узлу, а солнечное затмение может произойти только тогда, когда Новолуние находится вблизи (в пределах 17 ° 25 ') любого лунного узла.
Поскольку орбитальный самолет Луны прецессы в космосе лунные узлы также прецессия вокруг эклиптики, совершив один оборот (называемый драконий или же узловой период ) через 18,612958 лет (6798,383 дней). (Это не такая же длина, как у сарос.) Тот же самый цикл, измеренный относительно инерциальной системы отсчета, такой как Международная небесная справочная система (ICRS), а система координат относительно фиксированные звезды, составляет 18,599525 лет.
Оба солнечных затмения июля 2000 г. (на 1-й и 31-е дней) произошло примерно в то время, когда Луна находилась в восходящем узле. Затмения восходящего узла повторяются после одного драконий год в среднем, что составляет около 0,94901 Григорианский год, как и затмения с нисходящим узлом.
Имена и символы

В разных регионах мира узлы называются разными именами.
В средневековых текстах узлы упоминаются как рас ва дханав ат-тиннин в арабский. Рош Хатели У-Зенаво в иврит, и caput draconis (голова дракона) или cauda draconis (хвост дракона) в латинский.[1] Восходящий узел называется голова дракона с астрономический или же астрологический символ ☊ и нисходящий узел известен как хвост дракона с символом ☋.
В Индуистская астрономия, узлы рассматриваются с семь планет среди девяти Наваграхас; восходящий узел ☊ называется Раху а нисходящий узел ☋ называется Кету.[2] В Тибетская астрология (частично на основе Калачакра Тантра ) нисходящий узел называется Kalagni.[нужна цитата ]
Крайности склонения
Орбита Луны наклонена примерно на 5,14 ° к эклиптика; следовательно, Луна может быть примерно на 5 ° севернее или южнее эклиптики. Эклиптика наклонена примерно на 23,44 ° к небесный экватор, чей самолет перпендикуляр к оси вращения Земли. В результате один раз за 18,6-летний узловой период (когда восходящий узел орбиты Луны совпадает с весеннее равноденствие ), Луна склонение достигает максимума и минимума (северная и южная крайние точки): около 28,6 ° от небесного экватора. Следовательно, восход или закат луны азимут имеет свои северные и южные точки на горизонте; Луна в кульминация имеет свои самые низкие и самые высокие высота (когда тело проходит через меридиан ); и первые наблюдения Новолуние потенциально имеют свои последние времена. Более того, затмения Луной Плеяды звездное скопление, которое находится более чем на 4 ° к северу от эклиптики, происходит в течение сравнительно короткого периода один раз в каждый узловой период.
Влияние на приливы
В прецессия лунных узлов имеет небольшое влияние на Землю приливы – атмосферный, океанический, или же корковый.[3][4]Соединенные штаты. Национальное управление океанических и атмосферных исследований (NOAA) определяет средняя нижняя межень (MLLW) в определенном месте путем усреднения высоты самого низкого прилива, зарегистрированного в этом месте каждый день в течение 19-летнего периода регистрации, известного как Национальная эпоха приливных данных.[5] 19-летний период регистрации - это ближайший полный год к 18,6-летнему циклу лунных узлов.[6]
Смотрите также
Рекомендации
- ^ Села, Шломо (2003), Авраам ибн Эзра и рост средневековой древнееврейской науки, Серия Брилла по иудаике, 32, Лейден / Бостон: Brill, стр. 124–126, 244–245, ISBN 9789004129733
- ^ Хартнер, Вилли (1938), «Псевдопланетные узлы орбиты Луны в индуистской и исламской иконографии: вклад в историю древней и средневековой астрологии», Ars Islamica, 5 (2): 112–154, JSTOR 4520926
- ^ Годин, Г. (2015). Использование узловых поправок при вычислении гармонических констант. Международный гидрографический обзор, 63 (2). Извлекаются из https://journals.lib.unb.ca/index.php/ihr/article/view/23428
- ^ Kaye, Clifford A .; Стаки, Гэри В. (1973). «Узловой приливный цикл 18,6 года: его значение для кривых уровня моря на восточном побережье Соединенных Штатов и его значение для объяснения долгосрочных изменений уровня моря». Геология. 1 (3): 141. Дои:10.1130 / 0091-7613 (1973) 1 <141: NTCOYI> 2.0.CO; 2. ISSN 0091-7613.
- ^ "Приливные датумы". Приливы и течения. NOAA.
- ^ "Приливные датумы и их применение" (PDF). Приливы и течения. Сильвер Спринг, Мэриленд: NOAA (Специальная публикация NOS CO-OPS 1). Июнь 2000 г.
внешняя ссылка
- Апплет "Солнце и Луна", показывающий азимуты восхода / захода луны
- Астрономия Ответы: Какие состояния покоя Луны? Проверено 26 августа 2016.
- Затмения, космический часовой механизм древних
- Лунный и солнечный периоды, об инерциальной системе отсчета для измерения движения небесных тел.
- Средние лунные и солнечные периоды
