Максимальная подгруппа - Maximal subgroup
Эта статья нужны дополнительные цитаты для проверка. (Декабрь 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В математика, период, термин максимальная подгруппа используется для обозначения немного разных вещей в разных областях алгебра.
В теория групп, а максимальная подгруппа ЧАС из группа грамм это собственная подгруппа, таких, что нет собственной подгруппы K содержит ЧАС строго. Другими словами, ЧАС это максимальный элемент из частично заказанный набор собственных подгрупп грамм. Максимальные подгруппы интересны тем, что имеют прямую связь с примитивные представления перестановок из грамм. Они также много изучаются с целью теория конечных групп: см. например Подгруппа Фраттини, пересечение максимальных подгрупп.
В теория полугрупп, а максимальная подгруппа полугруппы S является подгруппой (то есть подполугруппой, которая образует группу при полугрупповой операции) S который не содержится должным образом в другой подгруппе S. Обратите внимание, что здесь нет требования, чтобы максимальная подгруппа была правильной, поэтому, если S на самом деле группа, то ее единственная максимальная подгруппа (как полугруппа) есть S сам. Рассмотрение подгрупп и, в частности, максимальных подгрупп полугрупп часто позволяет применять теоретико-групповые методы в теории полугрупп.[нужна цитата ] Существует однозначное соответствие между идемпотентные элементы полугруппы и максимальных подгрупп полугруппы: каждый идемпотентный элемент является элемент идентичности единственной максимальной подгруппы.
Существование максимальной подгруппы
Любая собственная подгруппа конечной группы содержится в некоторой максимальной подгруппе, поскольку собственные подгруппы образуют конечную частично заказанный набор при включении. Однако есть бесконечные абелевы группы которые не содержат максимальных подгрупп, например Prüfer group.[1]
Максимальная нормальная подгруппа
Аналогично нормальная подгруппа N из грамм называется максимальной нормальной подгруппой (или максимальной собственной нормальной подгруппой) группы грамм если N < грамм и нет нормальной подгруппы K из грамм такой, что N < K < грамм. У нас есть следующая теорема:
- Теорема: Нормальная подгруппа N группы грамм является максимальной нормальной подгруппой тогда и только тогда, когда частное грамм/N является просто.
Диаграммы Хассе
Эти Диаграммы Хассе показать решетки подгрупп из S4, Ди4 и Z23.
Максимальные подгруппы связаны с самой группой (наверху диаграммы Хассе) ребром диаграммы Хассе.
 |  | 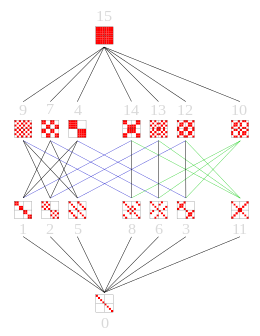 Z23 Максимальные подгруппы - семь Z22 |
