Нулевой вектор - Null vector
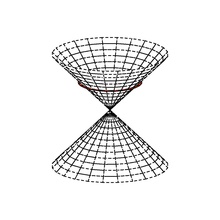
В математика, учитывая векторное пространство Икс с ассоциированным квадратичная форма q, написано (Икс, q), а нулевой вектор или же изотропный вектор ненулевой элемент Икс из Икс для которого q(Икс) = 0.
В теории настоящий билинейные формы, определенные квадратичные формы и изотропные квадратичные формы различны. Они отличаются тем, что только для последнего существует ненулевой нулевой вектор.
Квадратичное пространство (Икс, q) который имеет нулевой вектор, называется псевдоевклидово пространство.
Псевдоевклидово векторное пространство может быть разложено (неоднозначно) на ортогональные подпространства А и B, Икс = А + B, куда q положительно определен на А и отрицательно-определенный на B. В нулевой конус, или же изотропный конус, из Икс состоит из союза сбалансированных сфер:
Нулевой конус также является объединением изотропные линии через происхождение.
Примеры
В светоподобный векторов Пространство Минковского являются нулевыми векторами.
Четверка линейно независимый бикватернионы л = 1 + Здравствуй, п = 1 + гдж, м = 1 + гонконгский, и м∗ = 1 – гонконгский являются нулевыми векторами и { л, п, м, м∗ } может служить основа для подпространства, используемого для представления пространство-время. Нулевые векторы также используются в Формализм Ньюмана – Пенроуза подход к пространственно-временным многообразиям.[1]
А композиционная алгебра раскол когда он имеет нулевой вектор; в противном случае это алгебра с делением.
в Модуль Верма из Алгебра Ли есть нулевые векторы.
Рекомендации
- ^ Патрик Долан (1968) Решение уравнений Максвелла-Эйнштейна без сингулярностей, Коммуникации по математической физике 9 (2): 161–8, особенно 166, ссылка с Проект Евклид
- Дубровин, Б. А .; Фоменко, А.; Новиков, С. (1984). Современная геометрия: методы и приложения. Перевод Бернса, Роберт Г. Спрингер. п.50. ISBN 0-387-90872-2.
- Шоу, Рональд (1982). Линейная алгебра и представления групп. 1. Академическая пресса. п. 151. ISBN 0-12-639201-3.
- Невилл, Э. Х. (Эрик Гарольд) (1922). Пролегомены к аналитической геометрии в анизотропном евклидовом пространстве трех измерений. Издательство Кембриджского университета. п.204.


