Ортоцентрическая система - Orthocentric system

Ортоцентрическая система. Любая точка является ортоцентром треугольника, образованного тремя другими.

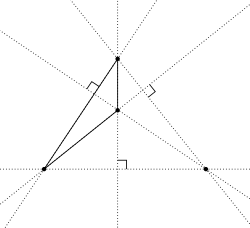
В геометрия, ортоцентрическая система это набор четырех точки на самолет, одним из которых является ортоцентр из треугольник образованный тремя другими.

Если четыре точки образуют ортоцентрическую систему, то каждый из четырех точек является ортоцентром трех других. Эти четыре возможных треугольника будут иметь одинаковые круг из девяти точек. Следовательно, все эти четыре возможных треугольника должны иметь окружности с тем же по окружности.

Обычный девятиточечный круг

Обычный девятиточечный круг, где O, O₄ и А₄ являются центром из девяти точек, центром описанной окружности и ортоцентром треугольника, образованного из трех других ортоцентрических точек A₁, А₂ и А₃.

Центр этого общего девятиконечного круга находится в точке центроид четырех ортоцентрических точек. Радиус общего круга из девяти точек - это расстояние от центра из девяти точек до середины любого из шести соединителей, которые соединяют любую пару ортоцентрических точек, через которые проходит общий круг из девяти точек. Круг из девяти точек также проходит через три ортогональных пересечения у основания высот четырех возможных треугольников.

Этот общий центр из девяти точек находится в средней точке соединителя, который соединяет любую ортоцентрическую точку с центром описанной окружности треугольника, образованного из трех других ортоцентрических точек.

Общая окружность из девяти точек касается всех 16 вписанных и вневписанных окружностей четырех треугольников, вершины которых образуют ортоцентрическую систему.^[1]

Обычный ортический треугольник, его центр и конец

Если шесть соединителей, соединяющих любую пару ортоцентрических точек, продлить до шести пересекающихся друг с другом прямых, они образуют семь точек пересечения. Четыре из этих точек являются исходными ортоцентрическими точками, а дополнительные три точки являются ортогональный перекрестки у подножия высоты. Соединение этих трех ортогональных точек в треугольник дает ортический треугольник это общее для всех четырех возможных треугольников, образованных из четырех ортоцентрических точек, взятых по три за раз.

В стимулятор этого общего ортического треугольника должна быть одна из четырех исходных ортоцентрических точек. Кроме того, три оставшихся точки становятся превосходители этого общего ортического треугольника. Ортоцентрическая точка, которая становится центром ортогонального треугольника, - это ортоцентрическая точка, ближайшая к общему центру из девяти точек. Это соотношение между orthic треугольником и четыре исходными orthocentric точек непосредственно приводят к тому, что вписанные и центрам вневписанных окружностей опорного треугольника образуют orthocentric системы.^{[2]:стр.182}

Нормально различать одну из ортоцентрических точек от других, особенно ту, которая является центром ортогонального треугольника; это обозначено ЧАС как ортоцентр наружных три orthocentric точек, которые выбраны в качестве опорного треугольника ABC. В этой нормализованной конфигурации точка ЧАС всегда будет лежать в треугольнике ABC, и все углы треугольника ABC будет остро. Четыре возможных треугольника, упомянутых выше, тогда называются треугольниками. ABC, ABH, ACH, и BCH. Шесть упомянутых выше разъемов AB, AC, до н.э, AH, BH, и CH. Семь пересечений, упомянутых выше, А, B, C, ЧАС (исходные ортоцентрические точки) и ЧАС_А, ЧАС_B, ЧАС_C (основания высот треугольника ABC и вершины ортогонального треугольника).

Ортоцентрическая система и ее ортические оси

Ортическая ось, связанная с нормализованной ортоцентрической системой А, B, C, и ЧАС, где ABC является ссылка треугольника, является линией, которая проходит через три точки пересечения, образованная, когда каждая сторона треугольника orthic встречает каждую сторону опорного треугольника. Теперь рассмотрим три других возможных треугольника, ABH, ACH, и BCH. У каждого из них своя ортическая ось.

Линии Эйлера и гомотетические ортоцентрические системы

Ортоцентрическая система. Где O₁, O₂, O₃ и O₄ являются центрами описанной окружности четырех возможных треугольников, образованных ортоцентрическими точками A₁, А₂, А₃ и А₄.

Позволять векторов а, б, c и час определить положение каждой из четырех ортоцентрических точек и позволить п = (а + б + c + час) / 4 - вектор положения N, общего девятиточечного центра. Соедините каждую из четырех ортоцентрических точек с их общим центром из девяти точек и вытяните их на четыре линии. Эти четыре линии теперь представляют собой линии Эйлера четырех возможных треугольников, где расширенная линия HN линия Эйлера треугольника ABC и расширенная линия AN это Линия Эйлера треугольника BCH и т.д. Если точка п выбирается на прямой Эйлера HN справочного треугольника ABC с вектором положения п такой, что п = п + α (час − п), где α - чистая постоянная, не зависящая от положения четырех ортоцентрических точек и еще трех точек п_А, п_B, п_C такой, что п_а = п + α (а − п) и т. д., то п, п_А, п_B, п_C образуют ортоцентрическую систему. Эта сгенерированная ортоцентрическая система всегда гомотетичный к исходной системе из четырех точек с общим девятиточечным центром в качестве центра гомотетики, а α - отношением подобие.

Когда п выбран как центроид г, то α = −1/3. Когда п выбран в качестве центр окружности O, то α = −1 и порожденная ортоцентрическая система имеет вид конгруэнтный к исходной системе, а также является ее отражением относительно девятиточечного центра. В этой конфигурации п_А, п_B, п_C сформировать Треугольник Джонсона исходного контрольного треугольника ABC. Следовательно, окружности из четырех треугольников ABC, ABH, ACH, BCH все равны и образуют набор Джонсон круги как показано на схеме рядом.

Другие свойства

Четыре линии Эйлера ортоцентрической системы ортогональны четырем ортогональным осям ортоцентрической системы.

Шесть соединителей, которые соединяют любую пару из исходных четырех ортоцентрических точек, образуют пары соединителей, которые ортогональны друг другу, так что они удовлетворяют уравнениям расстояния

${ displaystyle AB ^ {2} + CH ^ {2} = AC ^ {2} + BH ^ {2} = BC ^ {2} + AH ^ {2} = 4R ^ {2}}$

где р это общий радиус описанной окружности четырех возможных треугольников. Эти уравнения вместе с закон синуса привести к идентичности

${ displaystyle { frac {BC} { sin {A}}} = { frac {AC} { sin {B}}} = { frac {AB} { sin {C}}} = { frac {HA} {| cos {A} |}} = { frac {HB} {| cos {B} |}} = { frac {HC} {| cos {C} |}} = 2R .}$

Теорема Фейербаха утверждает, что окружность из девяти точек касается вписанной и трех вневписанных окружностей контрольного треугольника. Поскольку окружность с девятью точками является общей для всех четырех возможных треугольников в ортоцентрической системе, она касается 16 окружностей, содержащих вписанные и вневписанные окружности четырех возможных треугольников.

Любая коника, проходящая через четыре ортоцентрические точки, может быть только прямоугольной. гипербола.Это является результатом конического теоремы Фейербаха о том, что говорится, что для всех circumconics эталонного треугольника, который также проходит через ортоцентр, то локус Из центра таких циркумкоников образует окружность с девятью точками, и что окружные коники могут быть только прямоугольными гиперболами. Географическое место перспективы этого семейства прямоугольных гипербол всегда будет лежать на четырех ортических осях. Таким образом, если прямоугольная гипербола проведена через четыре ортоцентрических точки, у нее будет один фиксированный центр на общей окружности из девяти точек, но у нее будет четыре перспективы, по одному на каждой из ортоцентрических осей четырех возможных треугольников. Одна точки на девять точек окружности, которая является центром этой прямоугольной гиперболы будет иметь четыре различных определений, зависящие от каких из четырех возможных треугольников используются в качестве опорного треугольника.

Хорошо задокументированные прямоугольные гиперболы, проходящие через четыре ортоцентрические точки, - это гиперболы Фейербаха, Jeřábek и Киперт circumhyperbolas опорного треугольника ABC в нормализованной системе с H в качестве ортоцентра.

У четырех возможных треугольников есть набор из четырех инконикс известные как ортодонтические инконики, обладающие определенными свойствами. Контакты этих инкоников с четырьмя возможными треугольниками происходят в вершинах их общего ортического треугольника. В нормализованной ортоцентрической системе ортогонический инконик, касающийся сторон треугольника ABC, является эллипсом, а ортический инконик трех других возможных треугольников - гиперболами. Эти четыре ортодонтических инконика также имеют одно и то же Брианшон точка H, ортоцентрическая точка, ближайшая к общему центру из девяти точек. Центрами этих ортодонтических инкоников являются симедианные точки, K из четырех возможных треугольников.

Есть много задокументированных кубиков, которые проходят через опорный треугольник и его ортоцентр. Окружная кубика, известная как ортокубическая - K006, интересна тем, что она проходит через три ортоцентрические системы, а также через три вершины ортического треугольника (но не ортоцентр ортического треугольника). Три orthocentric системы вписанная и эксцентрики, опорный треугольник и его ортоцентр и, наконец, ортоцентр опорного треугольник вместе с тремя другими точками пересечения, что это имеет кубическое с окружностью опорного треугольника.

Любые два полярные круги двух треугольников ортоцентрической системы равны ортогональный.^{[2]:п. 177}

использованная литература

внешние ссылки

• Вайсштейн, Эрик В. «Ортоцентр». MathWorld.
• Вайсштейн, Эрик В. «Теорема Фейербаха». MathWorld.
• Вайсштейн, Эрик В. "Теорема Фейербаха о кониках". MathWorld.
• Вайсштейн, Эрик В. "Гипербола Фейербаха". MathWorld.
• Вайсштейн, Эрик В. «Джерабек Гипербола». MathWorld.
• Вайсштейн, Эрик В. «Кипертская гипербола». MathWorld.
• Вайсштейн, Эрик В. "Ортический инконик". MathWorld.
• Вайсштейн, Эрик В. "Ортическая ось". MathWorld.
• Вайсштейн, Эрик В. "Перспектор". MathWorld.
• Бернар Гиберт Окружно-кубический K006
• Кларк Кимберлинг "Энциклопедия треугольных центров ". (Перечисляет около 5000 интересных моментов, связанных с любым треугольником.)