Поверхность потенциальной энергии - Potential energy surface

А поверхность потенциальной энергии (PES) описывает энергию системы, особенно совокупности атомов, с точки зрения определенных параметров, обычно положения атомов. Поверхность может определять энергию как функцию одной или нескольких координат; если есть только одна координата, поверхность называется кривая потенциальной энергии или же энергетический профиль. Примером может служить Морзе / дальний потенциал.

Полезно использовать аналогию с ландшафтом: для системы с двумя степенями свободы (например, двумя длинами связей) значение энергии (аналогия: высота земли) является функцией двух длин связей (аналогия: координаты положения на местности).[1]

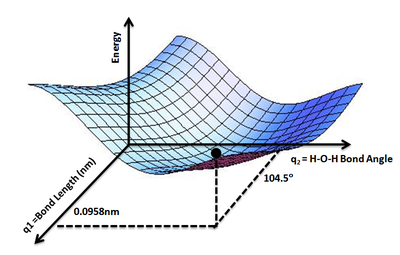
PES для молекулы воды: показывает минимум энергии, соответствующий оптимизированной молекулярной структуре для длины связи вода-O-H 0,0958 нм и угла связи H-O-H 104,5 °.

Концепция PES находит применение в таких областях, как химия и физика, особенно в теоретических разделах этих предметов. Его можно использовать для теоретического исследования свойств структур, состоящих из атомов, например, для нахождения минимальной энергетической формы молекулы или расчета скорости химической реакции.

Математическое определение и вычисление

Геометрия набора атомов может быть описана вектором, р, элементы которого представляют позиции атомов. Вектор р может быть набор Декартовы координаты атомов, или также может быть набором межатомных расстояний и углов.

Данный р, энергия как функция позиций, E(р), - значение E(р) для всех р представляет интерес. Используя аналогию с ландшафтом из введения, E дает высоту "энергетического ландшафта", так что концепция потенциальной энергии поверхность возникает.

Чтобы изучить химическую реакцию с использованием ППЭ в зависимости от положения атомов, необходимо рассчитать энергию для каждого интересующего расположения атомов. Методы расчета энергии конкретного атомного расположения атомов хорошо описаны в вычислительная химия статьи, и упор здесь будет на поиске приближений E(р) для получения детальной информации о энергетическом положении.

Для очень простых химических систем или когда делаются упрощающие приближения относительно межатомных взаимодействий, иногда можно использовать аналитически полученное выражение для энергии как функции положения атомов. Примером может служить Лондон -Айринг -Поланьи -Сато потенциал[2][3][4] для системы H + H2 как функция трех расстояний H-H.

Для более сложных систем расчет энергии определенного расположения атомов часто требует слишком больших вычислительных ресурсов, чтобы можно было представить крупномасштабные представления поверхности. Для этих систем возможный подход состоит в том, чтобы вычислить только сокращенный набор точек на PES, а затем использовать более дешевый метод интерполяции, например Интерполяция Шепарда, чтобы заполнить пробелы.[5]

Заявление

PES - это концептуальный инструмент для помощи в анализе молекулярная геометрия и химический динамика реакции. После того, как необходимые точки оценены на PES, точки можно классифицировать в соответствии с первой и второй производными энергии относительно положения, которые соответственно являются градиент и кривизна. Стационарные точки (или точки с нулевым градиентом) имеют физический смысл: минимумы энергии соответствуют физически стабильным химическим веществам и седловые точки соответствуют переходные состояния, самая высокая энергетическая точка на координата реакции (который представляет собой путь с наименьшей энергией, соединяющий химический реагент с химическим продуктом).

Привлекательные и отталкивающие поверхности

Поверхности потенциальной энергии для химических реакций можно классифицировать как привлекательный или же отталкивающий путем сравнения удлинений длин связей в активированном комплексе с таковыми у реагентов и продуктов.[6][7] Для реакции типа A + B-C → A-B + C удлинение длины связи для вновь образованной связи A-B определяется как R *AB = RAB - R0AB, где RAB - длина связи A — B в переходном состоянии, а R0AB в молекуле продукта. Аналогично для связи, которая разрывается в реакции, R *до н.э = Rдо н.э - R0до н.э, где R0до н.э относится к молекуле реагента.[8]

За экзотермические реакции, PES классифицируется как привлекательный (или же ранний спуск) если R *AB > R *до н.э, так что переходное состояние достигается при сближении реагентов. После переходного состояния длина связи A — B продолжает уменьшаться, так что большая часть выделяемой энергии реакции превращается в колебательный энергия связи A — B.[8][9] Примером может служить гарпунная реакция K + Br2 → K — Br + Br, в котором начальное дальнее притяжение реагентов приводит к активированному комплексу, напоминающему K+••• Br−••• Br.[8] Колебательно-возбужденные популяции молекул продукта могут быть обнаружены с помощью инфракрасного излучения. хемилюминесценция.[10][11]

В отличие от ППЭ для реакции H + Cl2 → HCl + Cl - это отталкивающий (или же поздний спуск) потому что R *HCl ClCl и переходное состояние достигается, когда продукты разделяются.[8][9] Для этой реакции, в которой атом A (здесь H) легче, чем B и C, энергия реакции выделяется в основном в виде поступательного кинетическая энергия продуктов.[8] Для реакции типа F + H2 → HF + H, в котором атом A тяжелее B и C, существует смешанный высвобождение энергии, как вибрационного, так и поступательного, даже несмотря на то, что ППЭ отталкивает.[8]

За эндотермические реакции, тип поверхности определяет тип энергии, который наиболее эффективно вызывает реакцию. Поступательная энергия реагентов наиболее эффективна для инициирования реакций с притягивающей поверхностью, в то время как колебательное возбуждение более эффективно для реакций с отталкивающей поверхностью.[8] Как пример последнего случая, реакция F + HCl (v = 1)[12] → Cl + HF примерно в пять раз быстрее, чем F + HCl (v = 0) → Cl + HF для той же полной энергии HCl.[13]

История

Концепция поверхности потенциальной энергии для химических реакций была впервые предложена французским физиком. Рене Марселин в 1913 г.[14] Первый полуэмпирический расчет поверхности потенциальной энергии был предложен для H + H2 реакция со стороны Генри Айринг и Майкл Поланьи в 1931 году. Эйринг использовал поверхности потенциальной энергии для расчета константы скорости реакции в теория переходного состояния в 1935 г.

Смотрите также

Рекомендации

  1. ^ Поверхность потенциальной энергии (реакции) в Сборнике химической терминологии, 2-е изд. («Золотая книга»). Составлено А. Д. Макнотом и А. Уилкинсоном. Научные публикации Блэквелла, Оксфорд (1997)
  2. ^ Сато, С. (1955). «Новый метод рисования поверхности потенциальной энергии». Бюллетень химического общества Японии. 28 (7): 450–453. Дои:10.1246 / bcsj.28.450.Сато, Шин (1955). «О новом методе рисования поверхности потенциальной энергии». Журнал химической физики. 23 (3): 592–593. Bibcode:1955ЖЧФ..23..592С. Дои:10.1063/1.1742043.
  3. ^ Кейт Дж. Лэйдлер, Химическая кинетика (3-е изд., Harper & Row, 1987) с. 68-70. ISBN  0-06-043862-2
  4. ^ Стейнфельд Дж. И., Франсиско Дж. С. и Hase W.L. Химическая кинетика и динамика (2-е изд., Prentice-Hall 1998) с.201-2. ISBN  0-13-737123-3
  5. ^ Подвижный метод наименьших квадратов улучшил интерполяцию Шепарда для быстрых маршевых и струнных методов, Burger SK1, Liu Y, Sarkar U, Ayers PW, J Chem Phys. 2009 130 (2) 024103. DOI: 10.1063 / 1.2996579.
  6. ^ Привлекательная поверхность потенциальной энергии в Сборнике химической терминологии, 2-е изд. («Золотая книга»). Составлено А. Д. Макнотом и А. Уилкинсоном. Научные публикации Блэквелла, Оксфорд (1997)
  7. ^ Отталкивающая поверхность потенциальной энергии в Сборнике химической терминологии, 2-е изд. («Золотая книга»). Составлено А. Д. Макнотом и А. Уилкинсоном. Научные публикации Блэквелла, Оксфорд (1997)
  8. ^ а б c d е ж грамм Кейт Дж. Лэйдлер, Химическая кинетика (3-е изд., Harper & Row, 1987) с.461-8. ISBN  0-06-043862-2
  9. ^ а б Стейнфельд Дж. И., Франсиско Дж. С. и Hase W.L. Химическая кинетика и динамика (2-е изд., Прентис-Холл 1998) с.272-4 ISBN  0-13-737123-3
  10. ^ Стейнфельд Дж. И., Франсиско Дж. С. и Hase W.L. Химическая кинетика и динамика (2-е изд., Прентис-Холл 1998) с.263. ISBN  0-13-737123-3
  11. ^ Аткинс П. и де Паула Дж. Физическая химия (8-е изд., У. Х. Фриман, 2006) с.886 ISBN  0-7167-8759-8
  12. ^ Здесь v - вибратонное квантовое число.
  13. ^ Аткинс П. и де Паула Дж. Физическая химия (8-е изд., У. Х. Фриман, 2006) с. 889-890. ISBN  0-7167-8759-8
  14. ^ Вычислительная химия: введение в теорию и приложения молекулярной и квантовой механики Эррол Г. Льюарс, 2-е изд. (Springer 2011) стр.21 ISBN  978-9048138616