Масштаб (карта) - Scale (map)

Графическая или линейчатая шкала. На карте также обычно указывается масштаб в числовом виде (например, «1: 50 000» означает, что один см на карте представляет 50 000 см реального пространства, что составляет 500 метров).

Штриховая шкала с номинальной шкалой, выраженной как «1 см = 6 км» и «1: 600 000» (эквивалентно, поскольку 6 км = 600 000 см).

В масштаб из карта это соотношение расстояния на карте до соответствующего расстояния на земле. Эта простая концепция осложняется кривизной Земля поверхность, которая заставляет масштаб изменяться на карте. Из-за этого различия понятие масштаба приобретает смысл двумя разными способами.

Первый способ - это соотношение размера создание глобуса размером с Землю. Генерирующий глобус - это концептуальная модель, в соответствии с которой Земля уменьшена и из которой строится карта. прогнозируемый. Отношение размера Земли к размеру генерирующего шара называется номинальная шкала (= основная шкала = представительная фракция). На многих картах указан номинальный масштаб и даже может отображаться гистограмма (иногда просто «шкала»), чтобы представить это.

Вторая особая концепция масштаба относится к вариациям масштаба на карте. Это отношение шкалы нанесенной точки к номинальной шкале. В данном случае «масштаб» означает масштаб (= шкала баллов = конкретный масштаб).

Если область карты достаточно мала, чтобы игнорировать кривизну Земли, например, на плане города, то в качестве масштаба можно использовать одно значение, не вызывая ошибок измерения. На картах, покрывающих большие площади или всю Землю, масштаб карты может быть менее полезным или даже бесполезным для измерения расстояний. Проекция карты становится критически важной для понимания того, как масштаб меняется по всей карте.^[1]^[2] Когда масштаб заметно меняется, это можно учитывать как масштабный коэффициент. Индикатриса Тиссо часто используется для иллюстрации изменения шкалы точек на карте.

История

Основы количественного масштабирования карты восходят к древний Китай с текстовыми свидетельствами того, что идея масштабирования карты была понята во втором веке до нашей эры. Древние китайские геодезисты и картографы обладали обширными техническими ресурсами, которые использовались для создания таких карт, как счетные стержни, плотницкая площадь s, отвес, компасы для рисования кругов и визирных тубусов для измерения наклона. Системы отсчета, постулирующие зарождающуюся систему координат для определения местоположения, были намекают древние китайские астрономы, которые делили небо на различные секторы или лунные ложи.^[3]

Китайский картограф и географ Пей Сю периода Троецарствия создал набор карт большой площади, которые были нарисованы в масштабе. Он разработал набор принципов, в которых подчеркивалась важность согласованного масштабирования, направленных измерений и корректировок в измерениях земли на местности, которая была нанесена на карту.^[3]

Терминология весов

Представление масштаба

Масштаб карты может быть выражен словами (лексический масштаб), в виде отношения или дроби. Примеры:

"от одного сантиметра до ста метров" или 1: 10 000 или 1/10 000

«один дюйм на одну милю» или 1: 63 360 или 1/63 360

«один сантиметр на тысячу километров», или 1: 100000000, или 1/100000000. (Соотношение обычно сокращается до 1: 100M)

Барная шкала против лексической шкалы

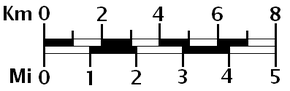
В дополнение к вышеперечисленному на многих картах есть один или несколько (графический) барные весы. Например, на некоторых современных британских картах есть три шкалы шкалы, по одной для километров, миль и морских миль.

Лексическую шкалу на языке, известном пользователю, может быть легче визуализировать, чем соотношение: если шкала является дюйм до двух миль и пользователь карты может видеть на карте две деревни, которые находятся на расстоянии около двух дюймов друг от друга, тогда легко вычислить, что деревни находятся на расстоянии около четырех миль друг от друга.

А лексический scale может вызвать проблемы, если оно выражено на языке, который пользователь не понимает, или в устаревших или плохо определенных единицах измерения. Например, масштаб от одного дюйма до фарлонг (1: 7920) будут понятны многим пожилым людям в странах, где Имперские единицы раньше преподавали в школах. Но масштаб одного мешок к одному лига может быть около 1: 144 000, в зависимости от картограф выбор из множества возможных определений лиги, и только меньшинство современных пользователей будут знакомы с используемыми единицами.

Большой, средний, маленький

Контрастировать с пространственный масштаб.

Карта классифицируется как малый масштаб или крупномасштабный или иногда средний масштаб. Малый масштаб относится к карты мира или карты больших регионов, таких как континенты или большие страны. Другими словами, они показывают большие участки земли на небольшом пространстве. Их называют мелкими, потому что представительная фракция относительно невелик.

На крупномасштабных картах мелкие области показаны более подробно, например на картах округов или городских планах. Такие карты называются крупномасштабными, потому что репрезентативная доля относительно велика. Например, план города, представляющий собой крупномасштабную карту, может иметь масштаб 1: 10 000, тогда как карта мира, которая представляет собой карту малого масштаба, может иметь масштаб 1: 100 000 000.

В следующей таблице описаны типичные диапазоны для этих шкал, но ее не следует рассматривать как авторитетную, поскольку нет стандарта:

Классификация	Ассортимент	Примеры
крупномасштабный	1:0 – 1:600,000	1: 0.00001 для карты вируса; 1: 5,000 для пешеходной карты города
средний масштаб	1:600,000 – 1:2,000,000	Карта страны
малый масштаб	1:2,000,000 – 1:∞	1: 50 000 000 для карты мира; 1:10²¹ для карты галактики

Иногда эти термины используются в абсолютном смысле таблицы, но иногда в относительном смысле. Например, картограф, чья работа относится исключительно к крупномасштабным картам (как указано в таблице выше), может называть карту размером 1: 500 000 мелкомасштабной.

В английском языке слово крупномасштабный часто используется в значении «обширный». Однако, как объяснялось выше, картографы используют термин «крупномасштабный» для обозначения Меньше обширные карты - те, которые показывают меньшую площадь. Карты, показывающие обширную территорию, являются картами «малого масштаба». Это может стать причиной недоумения.

Изменение масштаба

Нанесение на карту больших площадей вызывает заметные искажения, поскольку значительно сглаживает искривленную поверхность земли. Распространение искажений зависит от картографическая проекция. Масштаб варьируется в зависимости от карта, и указанный масштаб карты является только приблизительным. Это подробно обсуждается ниже.

Крупномасштабные карты без учета кривизны

Область, в которой Землю можно считать плоской, зависит от точности опрос измерения. Если измерять только с точностью до метра, то кривизна земли не обнаруживается на меридиональном расстоянии около 100 километров (62 миль) и на линии восток-запад около 80 км (на широта 45 градусов). При съемке с точностью до 1 миллиметра (0,039 дюйма) кривизна не обнаруживается на меридиан расстояние около 10 км и по линии восток-запад около 8 км.^[4] Таким образом, план Нью-Йорк с точностью до одного метра или план строительной площадки с точностью до одного миллиметра удовлетворяли бы указанным выше условиям без учета кривизны. Их можно рассматривать с помощью съемки на плоскости и наносить на карту с помощью масштабных чертежей, на которых любые две точки на одинаковом расстоянии на чертеже находятся на одинаковом расстоянии от земли. Истинные расстояния до земли рассчитываются путем измерения расстояния на карте и последующего умножения на обратный масштабной дроби или, что то же самое, просто использовать разделители для переноса расстояния между точками на карте в гистограмма на карте.

Снижение высоты

Изменение высоты от уровня земли до поверхности сферы или эллипсоида также изменяет масштаб измерения расстояния.^[5]

Балльная шкала (или конкретная шкала)

Как доказано Гаусс С Теорема Egregium, сферу (или эллипсоид) нельзя спроецировать на самолет без искажений. Обычно это иллюстрируется невозможностью разглаживать апельсиновую корку на плоской поверхности, не порвав и не деформируя ее. Единственное верное представление сферы в постоянном масштабе - это другая сфера, такая как глобус.

Учитывая ограниченный практический размер глобусов, мы должны использовать карты для детального картирования. Карты требуют проекций. Проекция подразумевает искажение: постоянное разделение на карте не соответствует постоянному разделению на земле. Хотя карта может отображать графическую шкалу, ее следует использовать с пониманием того, что она будет точной только на некоторых линиях карты. (Это обсуждается далее в примерах в следующих разделах.)

Позволять п быть точкой на широте ${ displaystyle varphi}$ и долгота ${ displaystyle lambda}$ на сфере (или эллипсоид ). Пусть Q - соседняя точка и пусть ${ displaystyle alpha}$ - угол между элементом PQ и меридианом в точке P: этот угол азимут угол элемента PQ. Пусть P 'и Q' - соответствующие точки на проекции. Угол между направлением P'Q и проекцией меридиана равен подшипник ${ displaystyle beta}$ . В общем ${ displaystyle alpha neq beta}$ . Комментарий: это точное различие между азимутом (на поверхности Земли) и пеленгом (на карте) наблюдается не повсеместно, многие авторы используют эти термины почти как синонимы.

Определение: то шкала баллов в P - это отношение двух расстояний P'Q 'и PQ в пределе, когда Q приближается к P. Мы запишем это как

{ displaystyle mu ( lambda, , varphi, , alpha) = lim _ {Q to P} { frac {P'Q '} {PQ}},}

где обозначение указывает, что шкала точек является функцией положения P, а также направления элемента PQ.

Определение: если P и Q лежат на одном меридиане ${ Displaystyle ( альфа = 0)}$ , то меридианная шкала обозначается ${ Displaystyle ч ( лямбда, , varphi)}$ .

Определение: если P и Q лежат на одной параллели ${ Displaystyle ( альфа = пи / 2)}$ , то параллельная шкала обозначается ${ Displaystyle к ( лямбда, , varphi)}$ .

Определение: если шкала зависит только от положения, а не от направления, мы говорим, что это изотропный и условно обозначим его значение в любом направлении параллельным масштабным коэффициентом ${ Displaystyle к ( лямбда, varphi)}$ .

Определение: Картографическая проекция называется конформный если угол между парой прямых, пересекающихся в точке P, такой же, как угол между проектируемыми линиями в спроецированной точке P ', для всех пар линий, пересекающихся в точке P. Конформная карта имеет изотропный масштабный коэффициент. И наоборот, изотропные масштабные коэффициенты на карте подразумевают конформную проекцию.

Изотропия масштаба означает, что маленький элементы растягиваются равномерно во всех направлениях, то есть форма небольшого элемента сохраняется. Это собственность ортоморфизм (от греч. «правильная форма»). Квалификация «малая» означает, что при некоторой заданной точности измерения не может быть обнаружено никаких изменений масштабного коэффициента по элементу. Поскольку конформные проекции имеют изотропный масштабный фактор, их также называют ортоморфные проекции. Например, проекция Меркатора является конформной, поскольку она построена так, чтобы сохранять углы, а ее масштабный коэффициент является изотопическим, только функцией широты: Меркатор делает сохранять форму на небольших участках.

Определение: на конформной проекции с изотропным масштабом точки с одинаковым масштабом могут быть объединены, чтобы сформировать изомасштабные линии. Они не отображаются на картах для конечных пользователей, но присутствуют во многих стандартных текстах. (См. Снайдер^[1] страницы 203–206.)

Репрезентативная фракция (RF) или основная шкала

При составлении уравнений любой проекции используются два соглашения. Например, равнопрямоугольная цилиндрическая проекция может быть записана как

картографы:

{ Displaystyle х = а лямбда}

{ Displaystyle у = а varphi}

математики:

{ Displaystyle х = лямбда}

{ displaystyle y = varphi}

Здесь мы примем первое из этих соглашений (следуя использованию Снайдера в обзорах). Очевидно, что приведенные выше уравнения проекции определяют положение огромного цилиндра, обернутого вокруг Земли и затем развернутого. Мы говорим, что эти координаты определяют карта проекции которые следует логически отличать от реальных напечатанный (или просмотренные) карты. Если определение шкалы в предыдущем разделе дано в терминах карты проекции, то можно ожидать, что масштабные коэффициенты будут близки к единице. Для нормальных касательных цилиндрических проекций масштаб вдоль экватора равен k = 1, и в целом масштаб изменяется по мере удаления от экватора. Анализ масштаба на карте проекции - это исследование изменения k от его истинного значения единицы.

Фактический печатные карты производятся из карты проекции постоянный масштаб обозначается соотношением, например 1: 100M (для карт всего мира) или 1: 10000 (для таких как планы городов). Чтобы избежать путаницы в использовании слова «масштаб», эта постоянная масштабная дробь называется представительная фракция (RF) печатной карты, и он должен быть идентифицирован с соотношением, напечатанным на карте. Фактические координаты распечатанной карты для равнопрямоугольной цилиндрической проекции:

распечатанная карта:

{ Displaystyle х = (РФ) а лямбда}

{ Displaystyle у = (РФ) а varphi}

Это соглашение позволяет четко различать собственное масштабирование проекции и масштабирование уменьшения.

С этого момента мы игнорируем RF и работаем с картой проекции.

Визуализация балльной шкалы: индикатриса Tissot

Тройная проекция Винкеля с Индикатриса Тиссо деформации

Рассмотрим небольшой круг на поверхности Земли с центром в точке P на широте ${ displaystyle varphi}$ и долгота ${ displaystyle lambda}$ . Поскольку шкала точек меняется в зависимости от положения и направления, проекция круга на проекции будет искажена. Tissot доказал, что, пока искажение не слишком велико, круг на проекции превратится в эллипс. Обычно размер, форма и ориентация эллипса изменяются в зависимости от проекции. Наложение этих эллипсов искажения на проекцию карты передает способ изменения шкалы точек на карте. Эллипс искажения известен как Индикатриса Тиссо. Показанный здесь пример - Проекция винкеля трипеля, стандартная проекция для карт мира, сделанная Национальное географическое общество. Минимальные искажения наблюдаются на центральном меридиане на 30 градусах широты (северная и южная). (Другие примеры^[6]^[7]).

Балльная шкала для нормальных цилиндрических проекций сферы

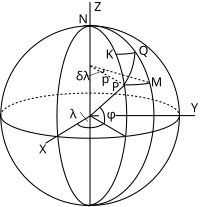
Ключ к количественный понимание масштаба заключается в рассмотрении бесконечно малого элемента на сфере. На рисунке показана точка P на широте ${ displaystyle varphi}$ и долгота ${ displaystyle lambda}$ на сфере. Точка Q находится на широте ${ displaystyle varphi + delta varphi}$ и долгота ${ displaystyle lambda + delta lambda}$ . Линии PK и MQ являются дуги меридианов длины ${ displaystyle a , delta varphi}$ где ${ displaystyle a}$ - радиус сферы и ${ displaystyle varphi}$ в радианах. Прямые PM и KQ представляют собой дуги параллельных окружностей длины ${ Displaystyle (а соз varphi) дельта лямбда}$ с участием ${ displaystyle lambda}$ в радианах. При выводе точка свойство проекции в P достаточно взять бесконечно малый элемент PMQK поверхности: в пределе Q, приближающемся к P, такой элемент стремится к бесконечно малому плоскому прямоугольнику.

Бесконечно малые элементы на сфере и нормальная цилиндрическая проекция

Нормальные цилиндрические выступы шара имеют ${ Displaystyle х = а лямбда}$ и ${ displaystyle y}$ равняется только функции широты. Следовательно, бесконечно малый элемент PMQK на сфере проецируется на бесконечно малый элемент P'M'Q'K ', который является точный прямоугольник с основанием ${ Displaystyle дельта х = а , дельта лямбда}$ и высота ${ displaystyle delta y}$ . Сравнивая элементы на сфере и проекции, мы можем сразу вывести выражения для масштабных коэффициентов на параллелях и меридианах. (Обращение с масштабом в общем направлении можно найти ниже.)

параллельный масштабный коэффициент

{ displaystyle quad k ; = ; { dfrac { delta x} {a cos varphi , delta lambda ,}} = , sec varphi qquad qquad {}}

масштабный коэффициент меридиана

{ displaystyle quad h ; = ; { dfrac { delta y} {a , delta varphi ,}} = { dfrac {y '( varphi)} {a}}}

Обратите внимание, что коэффициент параллельного масштабирования ${ Displaystyle к = сек varphi}$ не зависит от определения ${ Displaystyle у ( varphi)}$ так что это то же самое для всех нормальных цилиндрических выступов. Полезно отметить, что

на широте 30 градусов параллельная шкала

{ displaystyle k = sec 30 ^ { circ} = 2 / { sqrt {3}} = 1,15}

на широте 45 градусов параллельная шкала

{ Displaystyle к = сек 45 ^ { circ} = { sqrt {2}} = 1,414}

на широте 60 градусов параллельная шкала

{ Displaystyle к = сек 60 ^ { circ} = 2}

на широте 80 градусов параллельная шкала

{ Displaystyle к = сек 80 ^ { circ} = 5,76}

на широте 85 градусов параллельная шкала

{ Displaystyle к = сек 85 ^ { circ} = 11,5}

Следующие ниже примеры иллюстрируют три нормальных цилиндрических выступа, и в каждом случае изменение масштаба в зависимости от положения и направления иллюстрируется использованием Индикатриса Тиссо.

Три примера нормальной цилиндрической проекции

Равнопрямоугольная проекция

Эквидистантная проекция с Индикатриса Тиссо деформации

В равнопрямоугольная проекция,^[1]^[2]^[4] также известная как Plate Carrée (по-французски «плоский квадрат») или (несколько ошибочно) эквидистантная проекция, определяется как

{ Displaystyle х = а лямбда,}

{ displaystyle y = a varphi,}

где ${ displaystyle a}$ - радиус сферы, ${ displaystyle lambda}$ долгота от центрального меридиана проекции (здесь принимается за гринвичский меридиан на ${ displaystyle lambda = 0}$ ) и ${ displaystyle varphi}$ это широта. Обратите внимание, что ${ displaystyle lambda}$ и ${ displaystyle varphi}$ выражены в радианах (полученные путем умножения степени на коэффициент ${ displaystyle pi}$ / 180). Долгота ${ displaystyle lambda}$ находится в диапазоне ${ displaystyle [- pi, pi]}$ и широта ${ displaystyle varphi}$ находится в диапазоне ${ Displaystyle [- пи / 2, пи / 2]}$ .

поскольку ${ Displaystyle у '( varphi) = 1}$ предыдущий раздел дает

параллельная шкала,

{ displaystyle quad k ; = ; { dfrac { delta x} {a cos varphi , delta lambda ,}} = , sec varphi qquad qquad {}}

меридианная шкала

{ displaystyle quad h ; = ; { dfrac { delta y} {a , delta varphi ,}} = , 1}

Для расчета шкалы в произвольном направлении см. добавление.

Рисунок иллюстрирует Индикатриса Tissot для этой проекции. На экваторе h = k = 1 и круговые элементы неискажены на выступе. На более высоких широтах круги искажаются в эллипс, задаваемый вытягиванием только в параллельном направлении: в меридиональном направлении искажения нет. Отношение большой оси к малой оси равно ${ displaystyle sec varphi}$ . Ясно, что площадь эллипса увеличивается во столько же раз.

Поучительно рассмотреть возможность использования линейчатых шкал, которые могут появиться на печатной версии этой проекции. Масштаб истинный (k = 1) на экваторе, так что умножение его длины на печатной карте на обратную величину RF (или главный масштаб) дает фактическую длину окружности Земли. Шкала шкалы на карте также нарисована в истинном масштабе, поэтому перенос расстояния между двумя точками на экваторе на шкалу шкалы дает правильное расстояние между этими точками. То же самое и с меридианами. На параллели, отличной от экватора, масштаб ${ displaystyle sec varphi}$ поэтому, когда мы переносим разделение с параллели на линейную шкалу, мы должны разделить расстояние шкалы на этот коэффициент, чтобы получить расстояние между точками при измерении вдоль параллели (которое не является истинным расстоянием вдоль большого круга). На линии под углом, скажем, 45 градусов ( ${ displaystyle beta = 45 ^ { circ}}$ ) шкала непрерывно изменяется с широтой, и перенос разделения вдоль линии на шкалу столбцов не дает никакого простого отношения к истинному расстоянию. (Но см. добавление ). Даже если бы мы могли вычислить расстояние по этой линии константы, ее актуальность сомнительна, поскольку такая линия на проекции соответствует сложной кривой на сфере. По этим причинам линейчатую шкалу на мелкомасштабных картах следует использовать с особой осторожностью.

Проекция Меркатора

Проекция Меркатора с Индикатриса Тиссо деформации. (На более высоких широтах искажения неограниченно возрастают)

В Проекция Меркатора отображает сферу в прямоугольник (бесконечной протяженности в ${ displaystyle y}$ -направление) уравнениями^[1]^[2]^[4]

{ Displaystyle х = а лямбда ,}

{ displaystyle y = a ln left [ tan left ({ frac { pi} {4}} + { frac { varphi} {2}} right) right]}

где, ${ displaystyle lambda ,}$ и ${ displaystyle varphi ,}$ такие же, как в предыдущем примере. поскольку ${ Displaystyle у '( varphi) = а сек varphi}$ масштабные коэффициенты:

параллельная шкала

{ displaystyle k ; = ; { dfrac { delta x} {a cos varphi , delta lambda ,}} = , sec varphi.}

меридианная шкала

{ displaystyle h ; = ; { dfrac { delta y} {a , delta varphi ,}} = , sec varphi.}

В математической добавление показано, что шкала в произвольном направлении также равна ${ displaystyle sec varphi}$ поэтому масштаб изотропен (одинаков во всех направлениях), его величина увеличивается с широтой как ${ displaystyle sec varphi}$ . На диаграмме Тиссо каждый бесконечно малый круговой элемент сохраняет свою форму, но с увеличением широты увеличивается все больше и больше.

Проекция равной площади Ламберта

Нормальная цилиндрическая равновеликая проекция Ламберта с Индикатриса Тиссо деформации

Проекция равной площади Ламберта отображает сферу в конечный прямоугольник уравнениями^[1]^[2]^[4]

{ Displaystyle х = а лямбда qquad qquad у = а грех varphi}

где, ${ displaystyle lambda}$ и ${ displaystyle varphi}$ такие же, как в предыдущем примере. поскольку ${ Displaystyle у '( varphi) = соз varphi}$ масштабные коэффициенты

параллельная шкала

{ displaystyle quad k ; = ; { dfrac { delta x} {a cos varphi , delta lambda ,}} = , sec varphi qquad qquad {}}

меридианная шкала

{ displaystyle quad h ; = ; { dfrac { delta y} {a , delta varphi ,}} = , cos varphi}

Приведен расчет балльной шкалы в произвольном направлении. ниже.

Вертикальная и горизонтальная шкалы теперь компенсируют друг друга (hk = 1), и на диаграмме Тиссо каждый бесконечно малый круговой элемент искажен в виде эллипса. такой же площадь как неискаженные круги на экваторе.

Графики масштабных коэффициентов

График показывает изменение масштабных коэффициентов для трех приведенных выше примеров. На верхнем графике показана функция изотропной шкалы Меркатора: масштаб на параллели такой же, как и на шкале меридиана. На других графиках показан масштабный коэффициент меридиана для равнопрямоугольной проекции (h = 1) и для равновеликой проекции Ламберта. Эти последние две проекции имеют параллельный масштаб, идентичный масштабу графика Меркатора. Что касается Ламберта, обратите внимание, что параллельный масштаб (как Меркатор A) увеличивается с широтой, а масштаб меридиана (C) уменьшается с широтой таким образом, что hk = 1, что гарантирует сохранение площади.

Изменение масштаба проекции Меркатора

Шкала точек Меркатора равна единице на экваторе, потому что она такова, что вспомогательный цилиндр, используемый в ее конструкции, является касательной к Земле на экваторе. По этой причине обычную проекцию следует называть касательная проекция. Масштаб меняется в зависимости от широты как ${ Displaystyle к = сек varphi}$ . поскольку ${ displaystyle sec varphi}$ стремится к бесконечности, когда мы приближаемся к полюсам, карта Меркатора сильно искажается на высоких широтах, и по этой причине проекция совершенно не подходит для карт мира (если мы не обсуждаем навигацию и румба ). Однако на широте около 25 градусов значение ${ displaystyle sec varphi}$ около 1,1, поэтому Меркатор является с точностью до 10% в полосе шириной 50 градусов с центром по экватору.Лучше использовать более узкие полоски: полоса шириной 16 градусов (с центром на экваторе) имеет точность в пределах 1% или 1 часть из 100.

Стандартным критерием для хороших крупномасштабных карт является то, что точность должна быть в пределах 4 частей на 10 000, или 0,04%, что соответствует ${ displaystyle k = 1.0004}$ . поскольку ${ displaystyle sec varphi}$ достигает этого значения в ${ displaystyle varphi = 1,62}$ градусов (см. рисунок ниже, красная линия). Поэтому касательная проекция Меркатора очень точна в пределах полосы шириной 3,24 градуса с центром на экваторе. Это соответствует расстоянию с севера на юг около 360 км (220 миль). Внутри этой полосы Меркатор находится очень хороший, очень точный и сохраняет форму, потому что он конформный (сохраняет угол). Эти наблюдения побудили к разработке поперечных проекций Меркатора, в которых меридиан рассматривается «как экватор» проекции, так что мы получаем точную карту в пределах небольшого расстояния от этого меридиана. Такие карты подходят для стран, ориентированных почти с севера на юг (например, Великобритания ) и набор из 60 таких карт используется для Универсальная поперечная проекция Меркатора (UTM). Обратите внимание, что в обеих этих проекциях (которые основаны на различных эллипсоидах) уравнения преобразования для x и y и выражение для масштабного коэффициента являются сложными функциями как широты, так и долготы.

Изменение масштаба около экватора для касательной (красная) и секущей (зеленая) проекций Меркатора.

Секущие или модифицированные проекции

Основная идея секущей проекции состоит в том, что сфера проецируется на цилиндр, который пересекает сферу по двум параллелям, например ${ displaystyle varphi _ {1}}$ север и юг. Ясно, что масштаб теперь верен на этих широтах, тогда как параллели ниже этих широт сужаются проекцией, и их (параллельный) масштабный коэффициент должен быть меньше единицы. В результате отклонение шкалы от единицы уменьшается в более широком диапазоне широт.

Например, одна возможная секущая проекция Меркатора определяется следующим образом:

{ displaystyle x = 0,9996a lambda qquad qquad y = 0,9996a ln left ( tan left ({ frac { pi} {4}} + { frac { varphi} {2}}) верно-верно).}

Числовые множители не изменяют форму проекции, но это означает, что изменяются масштабные коэффициенты:

секущая шкала Меркатора,

{ displaystyle quad k ; = 0,9996 сек varphi.}

Таким образом

масштаб на экваторе 0,9996,
масштаб k = 1 на широте, заданной формулой ${ displaystyle varphi _ {1}}$ где ${ displaystyle sec varphi _ {1} = 1 / 0,9996 = 1,00004}$ так что ${ displaystyle varphi _ {1} = 1,62}$ градусы
k = 1.0004 на широте ${ displaystyle varphi _ {2}}$ данный ${ displaystyle sec varphi _ {2} = 1.0004 / 0.9996 = 1.0008}$ для которого ${ displaystyle varphi _ {2} = 2,29}$ градусов. Следовательно, проекция имеет ${ displaystyle 1$ , то есть точность 0,04% на более широкой полосе в 4,58 градуса (по сравнению с 3,24 градуса для касательной формы).

Это иллюстрируется нижней (зеленой) кривой на рисунке в предыдущем разделе.

Такие узкие зоны высокой точности используются в проекции UTM и британской OSGB, обе из которых являются секущими, поперечными по Меркатору на эллипсоиде со шкалой постоянной центрального меридиана на ${ displaystyle k_ {0} = 0,9996}$ . Изомасштабные линии с ${ displaystyle k = 1}$ представляют собой слегка изогнутые линии примерно в 180 км к востоку и западу от центрального меридиана. Максимальное значение масштабного коэффициента составляет 1,001 для UTM и 1 0007 для OSGB.

Линии единичной шкалы на широте ${ displaystyle varphi _ {1}}$ (север и юг), где цилиндрическая проекционная поверхность пересекает сферу, являются стандартные параллели секущей проекции.

Пока узкая полоса с ${ displaystyle | k-1 | <0,0004}$ Это важно для высокоточного картографирования в крупном масштабе, для карт мира используются более широко разнесенные стандартные параллели, чтобы контролировать изменение масштаба. Примеры

Behrmann со стандартными параллелями на 30N, 30S.
Галл равновеликий со стандартными параллелями на 45N, 45S.

Изменение масштаба для равновеликих проекций Ламберта (зеленый) и Галла (красный).

Графики масштаба для последнего показаны ниже в сравнении с масштабными коэффициентами равной площади Ламберта. В последнем случае экватор представляет собой единую стандартную параллель, и параллельный масштаб увеличивается с k = 1, чтобы компенсировать уменьшение масштаба меридиана. Для Галла параллельный масштаб уменьшается на экваторе (до k = 0,707), в то время как масштаб меридиана увеличивается (до k = 1,414). Это приводит к грубому искажению формы в проекции Галла-Петерса. (На земном шаре длина Африки равна ширине). Обратите внимание, что шкала меридиана и параллели равны единице на стандартных параллелях.

Математическое приложение

Бесконечно малые элементы на сфере и нормальная цилиндрическая проекция

Для нормальных цилиндрических проекций геометрия бесконечно малых элементов дает

{ displaystyle { text {(a)}} quad tan alpha = { frac {a cos varphi , delta lambda} {a , delta varphi}},}

{ displaystyle { text {(b)}} quad tan beta = { frac { delta x} { delta y}} = { frac {a , delta lambda} { delta y }}.}

Отношения между углами ${ displaystyle beta}$ и ${ displaystyle alpha}$ является

{ displaystyle { text {(c)}} quad tan beta = { frac {a sec varphi} {y '( varphi)}} tan alpha. ,}

Для проекции Меркатора ${ Displaystyle у '( varphi) = а сек varphi}$ давая ${ Displaystyle альфа = бета}$ : углы сохранены. (Это неудивительно, поскольку это отношение используется для вывода Меркатора). Для эквидистантной проекции и проекции Ламберта имеем ${ Displaystyle у '( varphi) = а}$ и ${ Displaystyle у '( varphi) = а соз varphi}$ соответственно так отношения между ${ displaystyle alpha}$ и ${ displaystyle beta}$ зависит от широты ${ displaystyle varphi}$ . Обозначим шкалу в точке P, когда бесконечно малый элемент PQ образует угол ${ Displaystyle альфа ,}$ с меридианом ${ displaystyle mu _ { alpha}.}$ Дается соотношением расстояний:

{ displaystyle mu _ { alpha} = lim _ {Q to P} { frac {P'Q '} {PQ}} = lim _ {Q to P} { frac { sqrt { delta x ^ {2} + delta y ^ {2}}} { sqrt {a ^ {2} , delta varphi ^ {2} + a ^ {2} cos ^ {2} varphi , delta lambda ^ {2}}}}.}

Настройка ${ Displaystyle дельта х = а , дельта лямбда}$ и заменяя ${ displaystyle delta varphi}$ и ${ displaystyle delta y}$ из уравнений (a) и (b) соответственно дает

{ displaystyle mu _ { alpha} ( varphi) = sec varphi left [{ frac { sin alpha} { sin beta}} right].}

Для проекций, отличных от проекций Меркатора, мы должны сначала вычислить ${ displaystyle beta}$ от ${ displaystyle alpha}$ и ${ displaystyle varphi}$ используя уравнение (c), прежде чем мы сможем найти ${ displaystyle mu _ { alpha}}$ . Например, равнопрямоугольная проекция имеет ${ Displaystyle у '= а}$ так что

{ Displaystyle загар бета = сек варфи загар альфа. ,}

Если рассматривать линию постоянного наклона ${ displaystyle beta}$ на проекции соответствующие значения ${ displaystyle alpha}$ и масштабный коэффициент вдоль линии являются сложными функциями ${ displaystyle varphi}$ . Не существует простого способа перенести общее конечное разделение на линейную шкалу и получить значимые результаты.

Символ отношения

В то время двоеточие часто используется для выражения соотношений, Unicode может выражать символ, характерный для соотношений, будучи слегка приподнятым: U + 2236 ∶ СООТНОШЕНИЕ (HTML∶ · & соотношение;).

Смотрите также

использованная литература

^ ^а ^б ^c ^d ^е Снайдер, Джон П. (1987). Картографические проекции - рабочее руководство. Профессиональный документ геологической службы США 1395. Типография правительства США, Вашингтон, округ КолумбияЭту статью можно скачать с Страницы USGS. Он дает полную информацию о большинстве прогнозов вместе с вводными разделами, но он не выводит какие-либо прогнозы из первых принципов. Вывод всех формул для проекции Меркатора можно найти в Проекции Меркатора.
^ ^а ^б ^c ^d Сглаживание Земли: две тысячи лет картографических проекций, Джон П. Снайдер, 1993, стр. 5-8, ISBN 0-226-76747-7. Это обзор практически всех известных прогнозов от древности до 1993 года.
^ ^а ^б Селин, Хелайн (2008). Энциклопедия истории науки, техники и медицины в незападных культурах. Springer (опубликовано 17 марта 2008 г.). п. 567. ISBN 978-1402049606.
^ ^а ^б ^c ^d Осборн, Питер (2013), Проекции Меркатора, Дои:10.5281 / zenodo.35392. (Дополнения: Файлы Maxima и Латексный код и цифры )
^ «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2014-08-27. Получено 2014-08-26.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)
^ Примеры индикатрисы Тиссо. Некоторые иллюстрации Tissot Indicatrix применяются к различным проекциям, кроме обычных цилиндрических.
^ Другие примеры индикатрисы Tissot в Wikimedia Commons.

[snyder-1] а ^б ^c ^d ^е Снайдер, Джон П. (1987). Картографические проекции - рабочее руководство. Профессиональный документ геологической службы США 1395. Типография правительства США, Вашингтон, округ КолумбияЭту статью можно скачать с Страницы USGS. Он дает полную информацию о большинстве прогнозов вместе с вводными разделами, но он не выводит какие-либо прогнозы из первых принципов. Вывод всех формул для проекции Меркатора можно найти в Проекции Меркатора.

[flattening-2] а ^б ^c ^d Сглаживание Земли: две тысячи лет картографических проекций, Джон П. Снайдер, 1993, стр. 5-8, ISBN 0-226-76747-7. Это обзор практически всех известных прогнозов от древности до 1993 года.

[Selin_2008_567-3] а ^б Селин, Хелайн (2008). Энциклопедия истории науки, техники и медицины в незападных культурах. Springer (опубликовано 17 марта 2008 г.). п. 567. ISBN 978-1402049606.

[merc-4] а ^б ^c ^d Осборн, Питер (2013), Проекции Меркатора, Дои:10.5281 / zenodo.35392. (Дополнения: Файлы Maxima и Латексный код и цифры )

[5] «Архивная копия» (PDF). Архивировано из оригинал (PDF) на 2014-08-27. Получено 2014-08-26.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)

[6] Примеры индикатрисы Тиссо. Некоторые иллюстрации Tissot Indicatrix применяются к различным проекциям, кроме обычных цилиндрических.

[7] Другие примеры индикатрисы Tissot в Wikimedia Commons.

[1]

[2]

[3]

[4]

[5]

[6]

[7]