Соленоидальное векторное поле - Solenoidal vector field

Пример соленоидального векторного поля, ${ Displaystyle mathbf {v} (х, y) = (y, -x)}$

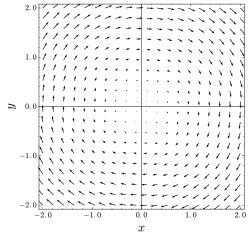
В векторное исчисление а соленоидальное векторное поле (также известный как несжимаемое векторное поле, а векторное поле без дивергенции, или поперечное векторное поле ) это векторное поле v с расхождение ноль во всех точках поля:

${ Displaystyle набла cdot mathbf {v} = 0. ,}$

Распространенный способ выразить это свойство - сказать, что поле не имеет источников или стоков. В полевые линии соленоидального поля являются замкнутыми контурами или оканчиваются на бесконечности.

Характеристики

В теорема расходимости дает эквивалентное интегральное определение соленоидального поля; а именно, что для любой замкнутой поверхности чистый полный поток через поверхность должен быть равен нулю:

${ Displaystyle mathbf {v} cdot , d mathbf {S} = 0}$,

куда ${ displaystyle d mathbf {S}}$ является внешней нормалью к каждому элементу поверхности.

В основная теорема векторного исчисления утверждает, что любое векторное поле может быть выражено как сумма безвихревый и соленоидальное поле. Условие нулевой дивергенции выполняется, когда векторное поле v имеет только векторный потенциал компонент, потому что определение векторного потенциала А в качестве:

${ Displaystyle mathbf {v} = набла раз mathbf {A}}$

автоматически приводит к личность (как можно показать, например, используя декартовы координаты):

${ displaystyle nabla cdot mathbf {v} = nabla cdot ( nabla times mathbf {A}) = 0.}$

В разговаривать также имеет место: для любых соленоидальных v существует векторный потенциал А такой, что ${ displaystyle mathbf {v} = nabla times mathbf {A}.}$ (Строго говоря, это выполняется при соблюдении определенных технических условий на v, видеть Разложение Гельмгольца.)

Этимология

Соленоидный происходит от греческого слова, означающего соленоид, что является σωληνοειδ (sōlēnoeidēs), что означает трубчатый, от σωλην (sōlēn) или труба. В данном контексте «соленоид» означает «ограниченный, как в трубе, с фиксированным объемом».

Примеры

• В магнитное поле B (видеть Уравнения Максвелла )
• В скорость поле поток несжимаемой жидкости
• В завихренность поле
• В электрическое поле E в нейтральных регионах (${ displaystyle rho _ {e} = 0}$);
• В плотность тока J где плотность заряда не меняется, ${ displaystyle { frac { partial rho _ {e}} { partial t}} = 0}$.
• В магнитный векторный потенциал А в кулоновской калибровке

Смотрите также

• Продольные и поперечные векторные поля
• Функция потока
• Консервативное векторное поле

Рекомендации

• Арис, Резерфорд (1989), Векторы, тензоры и основные уравнения механики жидкости, Дувр, ISBN  0-486-66110-5