Универсальный код (сжатие данных) - Universal code (data compression)
Эта статья нужны дополнительные цитаты для проверка. (Ноябрь 2011 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
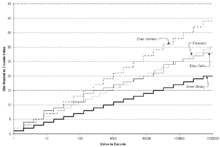

В Сжатие данных, а универсальный код для целых чисел - это код префикса который отображает положительные целые числа на двоичные кодовые слова с дополнительным свойством, которое независимо от истинного распределение вероятностей на целых числах, пока распределение является монотонным (т. е. п(я) ≥ п(я + 1) для всех положительныхя), ожидал длины кодовых слов находятся в пределах постоянного множителя ожидаемых длин, которые оптимальный код для этого распределения вероятностей было бы назначено. Универсальный код асимптотически оптимальный если соотношение между фактическим и оптимальным ожидал длина ограничена функцией информационная энтропия кода, который, помимо того, что он ограничен, приближается к 1, когда энтропия приближается к бесконечности.
В общем, большинство префиксных кодов для целых чисел присваивают более длинные кодовые слова более крупным целым числам. Такой код можно использовать для эффективной передачи сообщения, составленного из набора возможных сообщений, путем простого упорядочивания набора сообщений путем уменьшения вероятности и последующей отправки индекса предполагаемого сообщения. Универсальные коды обычно не используются для точно известных распределений вероятностей, и ни один универсальный код не известен как оптимальный для любого распределения, используемого на практике.
Универсальный код не следует путать с универсальное исходное кодирование, в котором метод сжатия данных не обязательно должен быть фиксированным префиксным кодом, а соотношение между фактической и оптимальной ожидаемой длиной должно приближаться к единице. Однако обратите внимание, что асимптотически оптимальный универсальный код можно использовать на независимые одинаково распределенные источники, используя все более крупные блоки, как метод универсального исходного кода.
Универсальные и неуниверсальные коды
Это несколько универсальных кодов для целых чисел; звездочка (* ) обозначает код, который можно тривиально переформулировать в лексикографический порядок, а двойной кинжал (‡ ) указывает на асимптотически оптимальный код:
- Гамма-кодирование Элиаса *
- Дельта-кодирование Элиаса * ‡
- Кодирование Элиаса Омеги *[требуется дальнейшее объяснение ] ‡
- Кодирование Exp-Golomb *, в котором гамма-кодирование Элиаса является частным случаем. (Используется в H.264 / MPEG-4 AVC )
- Кодирование Фибоначчи
- Кодирование Левенштейна * ‡, оригинальный универсальный метод кодирования [1]
- Байтовое кодирование где специальный битовый шаблон (минимум с двумя битами) используется для обозначения конца кода - например, если целое число закодировано как последовательность грызет представляющие цифры в база 15 вместо более естественного база 16, то наибольшее значение полубайта (то есть последовательность из четырех единиц в двоичном формате) может использоваться для обозначения конца целого числа.
- Количество переменной длины
Это неуниверсальные:
- Унарное кодирование, который используется в кодах Элиаса
- Кодирование риса, который используется в FLAC аудиокодек и в котором унарное кодирование является частным случаем
- Кодирование Голомба, в котором кодирование Райса и унарное кодирование являются частными случаями.
Их неуниверсальность можно наблюдать, заметив, что если что-либо из них используется для кодирования Распределение Гаусса – Кузьмина или Дзета-распределение с параметром s = 2 ожидаемая длина кодового слова бесконечна. Например, использование унарного кодирования для дзета-распределения дает ожидаемую длину
С другой стороны, использование универсального гамма-кодирования Элиаса для распределения Гаусса – Кузьмина приводит к ожидаемой длине кодового слова (около 3,51 бита), близкой к энтропии (около 3,43 бита).[2].
Отношение к практическому сжатию
Кодирование Хаффмана и арифметическое кодирование (когда их можно использовать) дают, по крайней мере, такое же, а часто и лучшее сжатие, чем любой универсальный код.
Однако универсальные коды полезны, когда нельзя использовать кодирование Хаффмана - например, когда неизвестна точная вероятность каждого сообщения, а известно только ранжирование их вероятностей.
Универсальные коды также полезны, когда коды Хаффмана неудобны. Например, когда передатчик, но не получатель, знает вероятности сообщений, кодирование Хаффмана требует накладных расходов на передачу этих вероятностей приемнику. Использование универсального кода не требует дополнительных затрат.
Каждый универсальный код, как и саморазграничивающий (префиксный) двоичный код, имеет собственное «подразумеваемое распределение вероятностей», задаваемое формулой п(я)=2−л(я) куда л(я) - длина яth кодовое слово и п(я) - вероятность соответствующего символа. Если фактические вероятности сообщения q(я) и Дивергенция Кульбака – Лейблера DKL(q||п) минимизируется кодом с л(я), то оптимальный код Хаффмана для этого набора сообщений будет эквивалентен этому коду. Точно так же, насколько код близок к оптимальному, можно измерить по этому расхождению. Поскольку универсальные коды проще и быстрее кодировать и декодировать, чем коды Хаффмана (что, в свою очередь, проще и быстрее, чем арифметическое кодирование ) универсальный код будет предпочтительнее в случаях, когда DKL(q||п) достаточно мала.[3]
Для любого геометрическое распределение (экспоненциальное распределение по целым числам) оптимальным является код Голомба. Для универсальных кодов неявное распределение приблизительно равно сила закона Такие как (точнее, Распространение Zipf ).Для Код Фибоначчи, неявное распределение приблизительно равно , с
куда это Золотое сечение. Для троичного код запятой (то есть кодирование в базе 3, представленное двумя битами на символ), неявное распределение является степенным законом с . Таким образом, эти распределения имеют почти оптимальные коды с соответствующими степенными законами.
внешняя ссылка
- Сжатие данных, Дебра А. Лелевер и Дэниел С. Хиршберг (Калифорнийский университет в Ирвине )
- Теория информации, логический вывод и алгоритмы обучения, к Дэвид Маккей, есть глава о кодах для целых чисел, включая введение в коды Элиаса.
- Кодирование целых чисел есть в основном англоязычные статьи по универсальным и другим целочисленным кодам.






