Суд над Бернулли - Википедия - Bernoulli trial

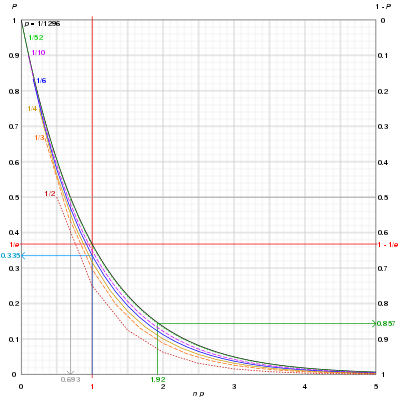
Графики вероятностей п из нет наблюдение независимых событий каждое из вероятностей п после п Испытания Бернулли против нп для различных п. Показаны три примера:
Синяя кривая: Бросок шестигранного кубика 6 раз дает 33,5% шанс, что 6 (или любое другое заданное число) никогда не выпадет; можно заметить, что как п увеличивается, вероятность 1 /п- случайное событие никогда не появляется после п пытается быстро сходится к 0.
Серая кривая: Чтобы получить шанс 50-50 бросить Yahtzee (5 кубических кубиков показывают одно и то же число) требует 0,69 × 1296 ~ 898 бросков.
Зеленая кривая: Вытягивание карты из колоды игральных карт без джокеров 100 (1,92 × 52) раз с заменой дает 85,7% шанс вытянуть туз пик хотя бы один раз.

В теории вероятность и статистика, а Бернулли суд (или же биномиальное испытание) является случайным эксперимент с двумя возможными результаты, «успех» и «неудача», в которых вероятность успеха одинакова каждый раз, когда проводится эксперимент.^[1] Он назван в честь Джейкоб Бернулли, швейцарский математик 17 века, проанализировавший их в своей Ars Conjectandi (1713).^[2]

Математическая формализация процесса Бернулли известна как Процесс Бернулли. Эта статья предлагает элементарное введение в концепцию, тогда как статья о процессе Бернулли предлагает более продвинутую трактовку.

Поскольку у испытания Бернулли есть только два возможных исхода, его можно сформулировать как вопрос «да или нет». Например:

Является ли верхняя карта перетасованной колоды тузом?
Был ли новорожденный ребенок девочкой? (Видеть соотношение полов человека.)

Следовательно, успех и неудача - это просто ярлыки для двух результатов, и их не следует толковать буквально. Термин «успех» в этом смысле означает результат, отвечающий определенным условиям, а не какое-либо моральное суждение. В более общем плане, учитывая любые вероятностное пространство, для любого мероприятие (набор результатов), можно определить испытание Бернулли, соответствующее тому, произошло событие или нет (событие или дополнительное событие ). Примеры испытаний Бернулли включают:

Подбрасывать монетку. В этом контексте лицевая сторона («решка») условно означает успех, а обратная сторона («решка») - неудача. А честная монета имеет вероятность успеха 0,5 по определению. В этом случае есть ровно два возможных исхода.
Прокатка умереть, где шестерка - «успех», а все остальное - «неудача». В этом случае есть шесть возможных исходов, и событие - шесть; дополнительное событие «не шестерка» соответствует пяти другим возможным исходам.
При проведении политического опрос общественного мнения, выбирая избирателя наугад, чтобы убедиться, проголосует ли этот избиратель «за» на предстоящем референдуме.

Определение

Независимые повторные испытания эксперимента с двумя возможными исходами называются испытаниями Бернулли. Назовите один результат «успехом», а другой - «неудачей». Позволять ${ displaystyle p}$ - вероятность успеха в суде Бернулли, и ${ displaystyle q}$ быть вероятностью отказа. Тогда вероятность успеха и вероятность неудачи суммируются в единицу, поскольку это взаимодополняющие события: «успех» и «неудача» равны взаимоисключающий и исчерпывающий. Таким образом, имеются следующие отношения:

{ Displaystyle p = 1-q, quad quad q = 1-p, quad quad p + q = 1.}

В качестве альтернативы они могут быть указаны в терминах шансы: заданная вероятность п успеха и q неудачи, шансы на находятся ${ displaystyle p: q}$ и шансы против находятся ${ displaystyle q: p.}$ Они также могут быть выражены в виде чисел путем деления, давая шансы на: ${ displaystyle o_ {f}}$ , и шансы против, ${ displaystyle o_ {a}:}$ ,

{ displaystyle { begin {align} o_ {f} & = p / q = p / (1-p) = (1-q) / q o_ {a} & = q / p = (1-p ) / p = q / (1-q) end {выровнено}}}

Это мультипликативные обратные, поэтому они умножаются на 1 со следующими соотношениями:

{ displaystyle o_ {f} = 1 / o_ {a}, quad o_ {a} = 1 / o_ {f}, quad o_ {f} cdot o_ {a} = 1.}

В случае, если суд Бернулли представляет собой событие из конечного числа равновероятные исходы, куда S результатов - успех и F результатов - неудача, шансы на ${ displaystyle S: F}$ и шансы против ${ displaystyle F: S.}$ Это дает следующие формулы для вероятности и шансов:

{ displaystyle { begin {align} p & = S / (S + F) q & = F / (S + F) o_ {f} & = S / F o_ {a} & = F / S end {выровнен}}}

Обратите внимание, что здесь шансы вычисляются путем деления количества исходов, а не вероятностей, но пропорция такая же, поскольку эти отношения различаются только умножением обоих членов на один и тот же постоянный коэффициент.

Случайные переменные описания испытаний Бернулли часто кодируются с использованием соглашения, что 1 = «успех», 0 = «неудача».

С испытанием Бернулли тесно связан биномиальный эксперимент, состоящий из фиксированного числа ${ displaystyle n}$ из статистически независимый Испытания Бернулли, каждое с вероятностью успеха ${ displaystyle p}$ , и считает количество успехов. Случайная величина, соответствующая биному, обозначается ${ Displaystyle В (п, р)}$ , и, как говорят, биномиальное распределение Вероятность точно ${ displaystyle k}$ успехи в эксперименте ${ Displaystyle В (п, р)}$ дан кем-то:

{ Displaystyle P (k) = {п выбрать k} p ^ {k} q ^ {n-k}}

куда ${ displaystyle {n select k}}$ это биномиальный коэффициент.

Испытания Бернулли также могут привести к отрицательные биномиальные распределения (которые подсчитывают количество успехов в серии повторных испытаний Бернулли до тех пор, пока не будет обнаружено определенное количество неудач), а также различные другие распределения.

Когда выполняется несколько испытаний Бернулли, каждое из которых имеет свою вероятность успеха, их иногда называют Пуассоновские испытания.^[3]

Пример: подбрасывание монет

Рассмотрим простой эксперимент, когда честная монета подбрасывается четыре раза. Найдите вероятность того, что ровно две подбрасывания завершатся орлом.

Решение

Для этого эксперимента давайте определим головы как успех и хвосты как отказ. Поскольку монета считается честной, вероятность успеха равна ${ displaystyle p = { tfrac {1} {2}}}$ . Таким образом, вероятность отказа, ${ displaystyle q}$ , дан кем-то

{ Displaystyle д = 1-р = 1 - { tfrac {1} {2}} = { tfrac {1} {2}}}

.

Используя приведенное выше уравнение, вероятность точно двух бросков из четырех, в результате которых выпадет решка, определяется следующим образом:

{ displaystyle { begin {align} P (2) & = {4 choose 2} p ^ {2} q ^ {4-2} & = 6 times left ({ tfrac {1} { 2}} right) ^ {2} times left ({ tfrac {1} {2}} right) ^ {2} & = { dfrac {3} {8}}. End { выровнено}}}

Смотрите также

внешняя ссылка

«Испытания Бернулли», Энциклопедия математики, EMS Press, 2001 [1994]
«Моделирование судебных процессов над Бернулли». math.uah.edu. Получено 2014-01-21.

[1] Папулис, А. (1984). «Испытания Бернулли». Вероятность, случайные величины и случайные процессы (2-е изд.). Нью-Йорк: Макгроу-Хилл. С. 57–63.

[2] Джеймс Виктор Успенский: Введение в математическую вероятность, McGraw-Hill, New York 1937, стр. 45.

[3] Раджив Мотвани и П. Рагхаван. Рандомизированные алгоритмы. Издательство Кембриджского университета, Нью-Йорк (Нью-Йорк), 1995, стр.67-68.

[1]

[2]

[3]