Закон Брэгга - Википедия - Braggs law

В физика, Закон Брэгга, или же Состояние Вульфа-Брэгга, частный случай Лауэ дифракция, дает углы когерентной и некогерентной рассеяние из кристаллической решетки. Когда Рентгеновские лучи инциденты на атом, они делают электронное облако двигаться, как и любой электромагнитная волна. В движение из этих обвинения повторно излучает волны с тем же частота, слегка размыты из-за множества эффектов; это явление известно как Рэлеевское рассеяние (или упругое рассеяние). Рассеянные волны могут сами рассеиваться, но предполагается, что этим вторичным рассеянием можно пренебречь.

Аналогичный процесс происходит при рассеянии нейтронных волн от ядра или последовательный вращение взаимодействие с непарным электрон. Эти переизлученные волновые поля вмешиваться друг с другом конструктивно или деструктивно (перекрывающиеся волны либо складываются вместе, чтобы получить более сильные пики, либо вычитаются друг из друга в некоторой степени), создавая дифракционную картину на детекторе или пленке. Результирующая волновая интерференция шаблон это основа дифракция анализ. Этот анализ называется Брэгговская дифракция.

История

Рентгеновские лучи взаимодействуют с атомами в кристалл.

Брэгговская дифракция (также называемая Брэгговская формулировка дифракции рентгеновских лучей) был впервые предложен Лоуренс Брэгг и его отец Уильям Генри Брэгг в 1913 г.^[1] в ответ на их открытие, что кристаллический твердые тела производили удивительные образцы отраженных Рентгеновские лучи (в отличие, скажем, от жидкости). Они обнаружили, что эти кристаллы при определенных длинах волн и углах падения дают интенсивные пики отраженного излучения.

Согласно 2θ отклонения, фазовый сдвиг вызывает конструктивные (левый рисунок) или деструктивные (правый рисунок) помехи.

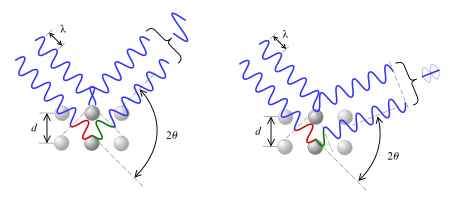
Лоуренс Брэгг объяснил этот результат, моделируя кристалл как набор дискретных параллельных плоскостей, разделенных постоянным параметром. d. Было высказано предположение, что падающее рентгеновское излучение будет создавать пик Брэгга, если их отражения от различных плоскостей конструктивно мешают. Помехи конструктивны, когда фазовый сдвиг кратен 2π; это условие можно выразить законом Брэгга (см. Условие Брэгга раздел ниже) и впервые был представлен Лоуренсом Брэггом 11 ноября 1912 г. Кембриджское философское общество.^[2][3] Несмотря на свою простоту, закон Брэгга подтвердил существование реальных частицы в атомном масштабе, а также предоставляет новый мощный инструмент для изучения кристаллы в виде рентгеновской и нейтронной дифракции. Лоуренс Брэгг и его отец Уильям Генри Брэгг были удостоены награды Нобелевская премия по физике в 1915 г. за их работу по определению кристаллических структур, начиная с NaCl, ZnS, и алмаз. Это единственная команда отца и сына, которая вместе побеждает. Лоуренсу Брэггу было 25 лет, что делало его самым молодым лауреатом Нобелевской премии по физике.

Концепция дифракции Брэгга в равной степени применима к нейтронная дифракция и электронная дифракция процессы.^[4] Обе нейтрон и длины волн рентгеновского излучения сравнимы с межатомными расстояниями (~ 150 пм) и, таким образом, являются отличным зондом для этого. шкала длины.

Условие Брэгга

Брэгговская дифракция. Два луча с одинаковой длиной волны и фазой приближаются к кристаллическому твердому телу и рассеиваются двумя разными атомами внутри него. Нижняя балка пересекает дополнительную длину 2dгрехθ. Конструктивная интерференция возникает, когда эта длина равна целому кратному длине волны излучения.

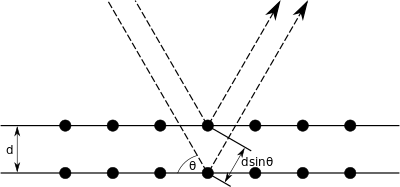
Брэгговская дифракция возникает, когда излучение с длиной волны, сравнимой с атомными расстояниями, рассеивается в зеркальный моды атомами кристаллической системы и претерпевает конструктивную интерференцию. Для кристаллического твердого тела волны рассеиваются на плоскостях решетки, разделенных межплоскостным расстоянием d. Когда рассеянные волны вмешиваться конструктивно они остаются в фазе, поскольку разница между длинами путей двух волн равна целое число кратное длине волны. Разность хода между двумя интерференционными волнами равна 2dгрех θ, куда θ это угол взгляда (см. рисунок справа и обратите внимание, что это отличается от принятого в Закон Снеллиуса куда θ отсчитывается от нормали к поверхности). Эффект конструктивной или деструктивной интерференции усиливается из-за кумулятивного эффекта отражения в последовательных кристаллографические плоскости (h, k, l) кристаллической решетки (как описано Обозначение Миллера ). Это приводит к закону Брэгга, который описывает условие на θ чтобы конструктивное вмешательство было максимально сильным:^[5]

${ Displaystyle 2d грех тета = п лямбда ,,}$

куда п положительное целое число и λ это длина волны падающей волны. Обратите внимание, что движущиеся частицы, в том числе электроны, протоны и нейтроны, имеют связанную длину волны, называемую длина волны де Бройля. Дифракционная картина получается путем измерения интенсивности рассеянных волн как функции угла рассеяния. Очень сильные интенсивности, известные как пики Брэгга, получаются на дифракционной картине в точках, где углы рассеяния удовлетворяют условию Брэгга. Как упоминалось во введении, это условие является частным случаем более общего Уравнения Лауэ, и можно показать, что уравнения Лауэ сводятся к условию Брэгга при дополнительных предположениях.

Явление дифракции Брэгга на кристаллической решетке имеет общие характеристики с явлением дифракции Брэгга на кристаллической решетке. тонкая пленка интерференции, который имеет идентичное состояние в пределе, когда показатели преломления окружающей среды (например, воздуха) и мешающей среды (например, масла) равны.

Эвристический вывод

Предположим, что один монохромный волна (любого типа) падает на выровненных плоскостях решетка точки, с разделением ${ displaystyle d}$, под углом ${ displaystyle theta}$. Точки А и C находятся в одной плоскости, и B находится на самолете ниже. Точки ABCC ' сформировать четырехугольник.

Будет разница в пути между луч это отражается AC ' и луч, который проходит AB, а затем отразился до н.э. Эта разница в пути

${ Displaystyle (AB + BC) - влево (AC ' вправо) ,.}$

Две отдельные волны прибудут в точку с одинаковым фаза, и, следовательно, пройти конструктивное вмешательство, тогда и только тогда, когда эта разность путей равна любому целому значению длина волны, т.е.

${ Displaystyle (AB + BC) - влево (AC ' вправо) = п лямбда ,,}$

где то же определение ${ displaystyle n}$ и ${ displaystyle lambda}$ применить, как указано выше.

Следовательно,

${ displaystyle AB = BC = { frac {d} { sin theta}} { text {and}} AC = { frac {2d} { tan theta}} ,,}$

откуда следует, что

${ displaystyle AC '= AC cdot cos theta = { frac {2d} { tan theta}} cos theta = left ({ frac {2d} { sin theta}} cos theta right) cos theta = { frac {2d} { sin theta}} cos ^ {2} theta ,.}$

Собираем все вместе,

${ displaystyle n lambda = { frac {2d} { sin theta}} - { frac {2d} { sin theta}} cos ^ {2} theta = { frac {2d} { sin theta}} left (1- cos ^ {2} theta right) = { frac {2d} { sin theta}} sin ^ {2} theta}$

что упрощает ${ Displaystyle п лямбда = 2d грех тета ,,}$ что является законом Брэгга.

Если бы дифрагировали только две плоскости атомов, как показано на рисунках, то переход от конструктивной интерференции к деструктивной был бы постепенным в зависимости от угла с мягким максимумы под углами Брэгга. Однако, поскольку многие атомные плоскости мешают реальным материалам, возникают очень острые пики, окруженные в основном деструктивными интерференциями.^[6]

Доступен строгий вывод из более общих уравнений Лауэ (см. Стр. Уравнения Лауэ ).

Брэгговское рассеяние видимого света коллоидами

А коллоидный кристалл очень упорядоченный массив частиц, который формируется на большом расстоянии (от нескольких миллиметры к одному сантиметр в длину); коллоидные кристаллы имеют внешний вид и свойства примерно аналогичный их атомным или молекулярным аналогам.^[7] Уже много лет известно, что благодаря отталкивающий Кулоновский взаимодействия, электрически заряженный макромолекулы в водный окружающая среда может демонстрировать большие расстояния кристалл -подобные корреляции, при этом расстояния между частицами часто значительно превышают диаметр отдельных частиц. Периодические массивы сферических частиц приводят к межклеточные пустоты (промежутки между частицами), которые действуют как естественный дифракционная решетка за видимые световые волны, когда межстраничный интервал такой же порядок величины как инцидент световая волна.^[8][9][10] В этих случаях в природе блестящие переливчатость (или игра цветов) объясняется дифракцией и конструктивное вмешательство видимых световых волн согласно закону Брэгга, в материи, аналогичной рассеяние из Рентгеновские лучи в кристаллическом твердом теле. Эффекты проявляются в видимых длинах волн, поскольку параметр разделения d намного больше, чем для настоящих кристаллов.

Объемные брэгговские решетки

Объемные брэгговские решетки (ВБГ) или объемные голографические решетки (VHG) состоят из объема, в котором наблюдается периодическое изменение показатель преломления. В зависимости от ориентации модуляции показателя преломления VBG может использоваться либо для передавать или же отражать небольшая пропускная способность длины волн.^[11] Закон Брэгга (адаптированный для объемной голограммы) определяет, на какой длине волны будет дифрагировать:^[12]

${ Displaystyle 2 Lambda sin ( theta + varphi) = m lambda _ {B} ,,}$

куда м - порядок Брэгга (положительное целое число), λ_B дифрагированный длина волны, Λ расстояние между кромками решетки, θ угол между падающим лучом и нормалью (N) входной поверхности и φ угол между нормалью и вектором решетки (K_грамм). Излучение, не соответствующее закону Брэгга, будет проходить через ВБГ недифрагированным. Выходную длину волны можно настроить на несколько сотен нанометров, изменив угол падения (θ). VBG используются для производства широко настраиваемый лазер источник или выполнить глобальный гиперспектральные изображения (видеть Фотон и др. ).

Правила отбора и практическая кристаллография

Закон Брэгга, как указано выше, можно использовать для определения шага решетки конкретного кубическая система через следующее отношение:

${ displaystyle d = { frac {a} { sqrt {h ^ {2} + k ^ {2} + ell ^ {2}}}} ,,}$

куда ${ displaystyle a}$ это шаг решетки кубический кристалл, и час, k, и ℓ являются Индексы Миллера самолета Брэгга. Объединение этой связи с законом Брэгга дает:

${ displaystyle left ({ frac { lambda} {2a}} right) ^ {2} = left ({ frac { lambda} {2d}} right) ^ {2} { frac { 1} {h ^ {2} + k ^ {2} + ell ^ {2}}}}$

Можно вывести правила отбора для Индексы Миллера для разных кубических Решетки Браве; здесь правила отбора для нескольких будут даны как есть.

Эти правила отбора можно использовать для любого кристалла с данной кристаллической структурой. KCl имеет гранецентрированную кубическую Решетка Браве. Однако K⁺ и Cl⁻ Ионы имеют одинаковое количество электронов и довольно близки по размеру, так что дифракционная картина становится практически такой же, как для простой кубической структуры с половиной параметра решетки. На правила выбора для других структур можно ссылаться в другом месте, или полученный. Шаг решетки для другого кристаллические системы можно найти здесь.

Смотрите также

• Самолет Брэгга
• Кристаллическая решетка
• Дифракция
• Распределенный брэгговский отражатель
  • Волоконная решетка Брэгга
• Динамическая теория дифракции
• Предел Хендерсона
• Условия Лауэ
• Порошковая дифракция
• Радарные ангелы
• Структурный фактор
• Рентгеновская кристаллография

Рекомендации

дальнейшее чтение

• Нил У. Эшкрофт и Н. Дэвид Мермин, Физика твердого тела (Харкорт: Орландо, 1976).
• Брэгг В. (1913). «Дифракция коротких электромагнитных волн на кристалле». Труды Кембриджского философского общества. 17: 43–57.

внешняя ссылка

• Нобелевская премия по физике - 1915 г.
• https://web.archive.org/web/20110608141639/http://www.physics.uoguelph.ca/~detong/phys3510_4500/xray.pdf
• Изучение кристаллографии